каково перемещение велосипедиста

Предлагаю игру: выбрать предмет в комнате и описать его местонахождение. Выполнить это так, чтобы угадывающий не смог ошибиться. Вышло? А что выйдет из описания, если другие тела не использовать? Останутся выражения: "слева от. ", "над . " и подобное. Положение тела можно задать только относительно какого-нибудь другого тела.

Местонахождение клада: "Стань у восточного угла крайнего дома села лицом на север и, пройдя 120 шагов, повернись лицом на восток и пройди 200 шагов. В этом месте вырой яму в 10 локтей и найдешь 100 слитков золота". Клад найти невозможно, иначе его давно откопали бы. Почему? Тело, относительно которого совершается описание не определено, неизвестно в каком селе находится тот самый дом. Необходимо точно определиться с телом, которое возьмется за основу нашего будущего описания. Такое тело в физике называется телом отсчета. Его можно выбрать произвольно. Например, попробуйте выбрать два различных тела отсчета и относительно их описать местонахождение компьютера в комнате. Выйдет два непохожих друг на друга описания.

Система координат

Рассмотрим картинку. Где находится дерево, относительно велосипедиста I, велосипедиста II и нас, смотрящих на монитор?

Относительно тела отсчета — велосипедист I — дерево находится справа, относительно тела отсчета — велосипедист II — дерево находится слева, относительно нас оно впереди. Одно и то же тело — дерево, находящееся постоянно в одном и том же месте, одновременно и "слева", и "справа" и "впереди". Проблема не только в том, что выбраны различные тела отсчета. Рассмотрим его расположение относительно велосипедиста I.

На этом рисунке дерево справа от велосипедиста I

На этом рисунке дерево слева от велосипедиста I

Дерево и велосипедист не меняли своего месторасположения в пространстве, однако дерево одновременно может быть "слева" и "справа". Для того, чтобы избавиться от неоднозначности описания самого направления, выберем определенное направление за положительное, противоположное выбранному будет отрицательным. Выбранное направление обозначают осью со стрелкой, стрелка указывает положительное направление. В нашем примере выберем и обозначим два направления. Слева направо (ось, по которой движется велосипедист), и от нас внутрь монитора к дереву — это второе положительное направление. Если первое, выбранное нами направление, обозначить за X, второе — за Y, получим двухмерную систему координат.

Относительно нас велосипедист движется в отрицательном направлении по оси X, дерево находится в положительном направлении по оси Y

Относительно нас велосипедист движется в положительном направлении по оси X, дерево находится в положительном направлении по оси Y

А теперь определите, какой предмет в комнате находится в 2 метрах в положительном направлении по оси X (справа от вас), и в 3 метрах в отрицательном направлении по оси Y (позади вас). (2;-3) — координаты этого тела. Первой цифрой "2" принято обозначать расположение по оси X, вторая цифра "-3" указывает расположение по оси Y. Она отрицательная, потому что по оси Y находится не в стороне дерева, а в противоположной стороне. После того, как выбрано тело отсчета и направления, месторасположение любого предмета будет описано однозначно. Если вы повернетесь спиной к монитору, справа и позади вас будет уже другой предмет, но и координаты у него будут другие (-2;3). Таким образом, координаты точно и однозначно определяют расположение предмета.

Пространство, в котором мы живем, — пространство трех измерений, как говорят, трехмерное пространство. Кроме того, что тело может находится "справа" ("слева"), "впереди" ("позади"), оно может быть еще "выше" или "ниже" вас. Это третье направление — принято обозначать его осью Z

Можно ли выбирать не такие направления осей? Можно. Но нельзя менять их направления в течение решения, например, одной задачи. Можно ли выбрать другие названия осей? Можно, но вы рискуете тем, что вас не поймут другие, лучше так не поступать. Можно ли поменять местами ось X с осью Y? Можно, но не путайтесь в координатах: (x;y).

При прямолинейном движении тела для определения его положения достаточно одной координатной оси.

Для описания движения на плоскости используется прямоугольная система координат, состоящая из двух взаимно перпендикулярных осей (декартовая система координат).

С помощью трехмерной системы координат можно определить положение тела в пространстве.

Система отсчета

Каждое тело в любой момент времени занимает определенное положение в пространстве относительно других тел. Определять его положение уже умеем. Если с течением времени положение тела не изменяется, то оно покоится. Если же с течением времени положение тела изменяется, то это означает, что тело движется. Все в мире происходит где-то и когда-то: в пространстве (где?) и во времени (когда?). Если к телу отсчета, системе координат, которые определяют положение тела, добавить способ измерения времени — часы, получим систему отсчета. При помощи которой можно оценить движется или покоится тело.

Относительность движения

Космонавт вышел в открытый космос. В состоянии покоя или движения он находится? Если рассматривать его относительно друга космонавта, находящегося рядом, он будет покоиться. А если относительно наблюдателя на Земле, космонавт движется с огромной скоростью. Аналогично с поездкой в поезде. Относительно людей в поезде вы неподвижно сидите и читаете книгу. Но относительно людей, которые остались дома, вы двигаетесь со скоростью поезда.

Примеры выбора тела отсчета, относительно которого на рисунке а) поезд движется (относительно деревьев), на рисунке б) поезд покоится относительно мальчика.

Сидя в вагоне, ожидаем отправления. В окне наблюдаем за электричкой на параллельном пути. Когда она начинает двигаться, трудно определить кто движется — наш вагон или электричка за окном. Для того, чтобы определиться, необходимо оценить движемся ли мы относительно других неподвижных предметов за окном. Мы оцениваем состояние нашего вагона относительно различных систем отсчета.

Изменение перемещения и скорости в разных системах отсчета

Перемещение и скорость изменяются при переходе из одной системы отсчета в другую.

Скорость человека относительно земли (неподвижной системы отсчета) различная в первом и втором случаях.

Правило сложения скоростей: Скорость тела относительно неподвижной системы отсчета — это векторная сумма скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной.

Аналогично вектора перемещения. Правило сложения перемещений: Перемещение тела относительно неподвижной системы отсчета — это векторная сумма перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной.

Пусть человек идет по вагону по направлению (или против) движения поезда. Человек — тело. Земля — неподвижная система отсчета. Вагон — подвижная система отсчета.

Вектора подвижной со и тела относительно подвижной со совпадают по направлению

Вектора подвижной со и тела относительно подвижной со противоположные по направлению

Изменение траектории в разных системах отсчета

Траектория движения тела относительна. Например, рассмотрим пропеллер вертолета, спускающегося на Землю. Точка на пропеллере описывает окружность в системе отсчета, связанного с вертолетом. Траектория движения этой точки в системе отсчета, связанной с Землей, представляет собой винтовую линию.

Поступательное движение

Движение тела — это изменение его положения в пространстве относительно других тел с течением времени. Каждое тело имеет определенные размеры, иногда разные точки тела находятся в разных местах пространства. Как же определить положение всех точек тела?

НО! Иногда нет необходимости указывать положение каждой точки тела. Рассмотрим подобные случаи. Например, это не нужно делать, когда все точки тела движутся одинаково.

Одинаково движутся все токи чемодана, машины.

Движение тела, при котором все его точки движутся одинаково, называется поступательным

Материальная точка

Не нужно описывать движение каждой точки тела и тогда, когда его размеры очень малы по сравнению с расстоянием, которое оно проходит. Например, корабль, преодолевающий океан. Астрономы при описании движения планет и небесных тел друг относительно друга не учитывают их размеров и их собственное движение. Несмотря на то, что, например, Земля громадная, относительно расстояния до Солнца она ничтожно мала.

Нет необходимости рассматривать движение каждой точки тела, когда они не влияют на движение тела всего целиком. Такое тело можно представлять точкой. Все вещество тела как бы сосредотачиваем в точку. Получаем модель тела, без размеров, но она имеет массу. Это и есть материальная точка.

Одно и то же тело при одних его движениях можно считать материальной точкой, при других — нельзя. Например, когда мальчик идет из дома в школу и при этом проходит расстояние 1 км, то в этом движении его можно считать материальной точкой. Но когда тот же мальчик выполняет зарядку, то точкой его считать уже нельзя.

Рассмотрим движущихся спортсменов

В этом случае можно спортсмена моделировать материальной точкой

В случае прыжка спортсмена в воду (рисунок справа) нельзя моделировать его в точку, так как от любого положения рук и ног зависит движение всего тела

Главное запомнить

1) Положение тела в пространстве определяется относительно тела отсчета;
2) Необходимо задать оси (их направления), т.е. систему координат, которая определяет координаты тела;
3) Движение тела определяется относительно системы отсчета;
4) В разных системах отсчета скорость тела может быть разной;
5) Что такое материальная точка

Видеодемонстрация относительности движения

Сложение скоростей

Более сложная ситуация сложения скоростей. Пусть человек переправляется на лодке через реку. Лодка — это исследуемое тело. Неподвижная система отсчета — земля. Подвижная система отсчета — река.

Скорость лодки относительно земли — это векторная сумма . Находится по закону параллелограмма, как гипотенуза двух катетов.

Упражнения

Относительно велосипедиста каждая машина движется. Машина относительно другой машины покоится. Велосипедист движется относительно машины.

Из центра горизонтально расположенного вращающегося диска по его поверхности пущен шарик. Каковы траектории шарика относительно Земли и диска?

Относительно Земли — спираль, относительно диска — прямая.

Чему равно перемещение какой-либо точки, находящейся на краю диска радиусом R при его повороте относительно подставки на 600? на 1800? Решить в системах отсчета, связанных с подставкой и диском.

В системе отсчета, связанной с подставкой, перемещения равны R и 2R. В системе отсчета, связанной с диском, перемещение все время равно нулю.

Почему дождевые капли в безветренную погоду оставляют наклонные прямые полосы на стеклах равномерно движущегося поезда?

В системе отсчета, связанной с Землей, траектория капли — вертикальная линия. В системе отсчета, связанной с поездом, движение капли по стеклу есть результат сложения двух прямолинейных и равномерных движений: поезда и равномерного падения капли в воздухе. Поэтому след капли на стекле наклонный.

Каким образом можно определить скорость бега, если тренироваться на беговой дорожке со сломанным автоматическим определением скорости? Ведь относительно стен зала не пробегаешь ни одного метра.

Определить скорость беговой ленты относительно стен зала.

Эскалатор метро движется вверх со скоростью 0,75 м/с. а) С какой скоростью и в каком направлении надо идти по эскалатору, чтобы быть все время на уровне одного из фонарей освещения туннеля? б) С какой скоростью относительно поднимающейся лестницы надо было бы передвигаться, чтобы опускаться вниз со скоростью пассажиров, неподвижно стоящих на другой опускающейся лестнице?

а) Вниз со скоростью 0,75 м/с; б) 1,5 м/с

Какую систему координат следует выбрать (одномерную, двухмерную, трехмерную) для определения положения таких тел: 1. трактор в поле; 2. поезд; 3. люстра в комнате; 4. лифт; 5. подводная лодка; 6. шахматная фигура

1. двухмерную; 2. одномерную; 3. двухмерную; 4. одномерную; 5. трехмерную; 6. двухмерную

Полная информация о знаке «Велосипедная дорожка»

Инфраструктура российских городов устроена таким образом, что далеко не везде есть велосипедные дорожки. Но в последнее время их становится больше, и у людей появляется возможность кататься в свободное время или ездить по делам на двухколёсном транспорте, не рискуя при этом. Конечно, передвижение такого рода подчиняется определённым правилам ПДД, и очень важно понимать информацию на дорожных знаках. Поэтому мы предлагаем вам познакомиться с видами велосипедных дорожек и узнать все об указателях.

Что такое велосипедная дорожка

Это и полоса для велосипедистов, выделенная на общей дороге, и специальная велосипедная дорожка, проложенная, например, в парке. В любом случае, она имеет собственную разметку, информационные знаки и правила передвижения. Визуально её также стараются обособить: выделить бордюром, газоном или полосой, замостить пешеходный тротуар другим материалом, чтобы люди не путались.

Большинство российских велодорожек не являются полноценной частью транспортной системы и предназначены только для прогулок, то есть перемещаясь только по ним, нельзя добраться до любой точки города. Вследствие такого неудобства велосипедисты при поездках по делам (например, за покупками) пользуются тротуарами и руководствуются правилами для пешеходов.

Виды велосипедных дорожек

В России есть три вида дорожек:

полоса для велосипедистов на общей проезжей части;
специальная дорожка только для велосипедистов и обладателей мопедов;
дорожка для велосипедистов и пешеходов.

Первый вариант заключается в том, что край дороги, по которой ездят машины, для велосипедистов выделен полосой и бордюром (не всегда). Пересекать эту границу автомобилисты и мотоциклисты не имеют права, также они должны уступать велосипедистам на перекрестках.

На улицах с односторонним движением дополнительная полоса для двухколесного безмоторного транспорта обозначается соответствующим знаком: в голубом квадрате, поделенном вдоль на два поля, изображается с одной стороны велосипед и короткая стрелка, а с другой – длинная стрелка. Это не только информирует велосипедистов о наличии удобного места для катания, но и предохраняет водителей машин от соблазна выехать на свободную полосу.

На улицах с двусторонним движением возможны варианты, когда велосипедные дорожки устраивают по обеим обочинам дороги, чтобы велосипедисты двигались навстречу транспорту, либо отделяют полосу с одной стороны бордюром и газоном, а её, в свою очередь, тоже разбивают на две полосы.

Место, где велосипедная дорожка пересекает основную проезжую часть, отмечается знаком квадратной формы с голубым фоном, поделенным поперек: сверху изображен велосипед и короткая стрелка, а снизу – длинная, или наоборот – в зависимости от направления движения.

Полоса на проезжей части – не слишком удобное и безопасное решение, поскольку некоторые водители стремятся то припарковаться на ней, то использовать, как пространство для обгона и прочих маневров. Также часто нарушается приоритет пересечения улицы.

Дорожка, совмещенная с пешеходной зоной, на порядок безопаснее. Кроме того, это самый распространенный вариант велодорожек в России. Эти участки отмечаются круглым знаком, где на синем фоне белой краской нарисован велосипед и фигурка человека. Чаще всего в подобных зонах нет ничего такого, что намекало бы на попытки муниципальных служб облегчить перемещение велосипедистов и пешеходов – это просто тротуары, где каждый передвигается, ориентируясь по ситуации и создавая другим неудобства.

Приоритет в данном случае остается за пешеходами, а велосипедисты вынуждены лавировать в их потоке. Установленный знак может всего лишь предупредить первых о внезапном появлении последних и проинформировать новичков-велосипедистов об их праве ездить по тротуару.

Самый предпочтительный, удобный и редкий вариант велодорожки – отдельная, самостоятельная, специальная зона, представляющая собой мини-копию проезжей части и разделенная на две полосы. Она отмечается круглым голубым знаком с изображением велосипеда и отгораживается от пешеходного тротуара бордюром.

Для такой велодорожки есть правило: по ней нельзя ходить пешком. Это, безусловно, снимает с велосипедиста скоростные ограничения и позволяет ему спокойно ездить, не боясь ежеминутно кого-то толкнуть. К сожалению, подобные зоны встречаются редко и располагаются на набережных курортных городов, в крупных парках и скверах и на территории спортивно-оздоровительных учреждений.

Характеристика и описание знака велосипедная дорожка

Дорожный знак, именуемый «Велосипедная дорожка», постоянно путают с другим – «Пересечение с велосипедной дорожкой».

Как выглядит тот и другой:

Предписывающий знак «Велосипедная дорожка» имеет круглую форму, голубой или светло-синий фон и белое изображение велосипеда в центре. Он вывешивается, чтобы сообщить водителям о том, что удобная проезжая часть, отделенная от основной газоном или бордюром, выделена не для них, и можно получить штраф за езду, а также о том, что если при повороте придется пересечь велодорожку, то нужно уступить велосипедистам. Для пешеходов такой знак – сигнал о том, что они не могут ходить по этой зоне без экстренной необходимости (когда отсутствует тротуар).
Треугольник с толстым красным абрисом, в котором на белом фоне изображен черный велосипед, называется «Пересечение с велосипедной дорожкой». Форма и цвет обозначают, что знак предупреждающий: он размещается неподалеку от того места, где с велодорожкой пересекается проезжая часть. Цель этого знака – призвать водителя сконцентрировать внимание и соблюдать осторожность. В этом случае приоритет движения остается за автомобилистами, но, по факту, если велосипедисты не настроены останавливаться, лучше уступить.

Знак под названием «Конец велосипедной дорожки» представляет собой перечеркнутую копию обозначения «Велосипедная дорожка». С момента встречи с этим знаком велосипедист теряет все преимущества на перекрестках и подвергается опасности, если продолжает ехать по краю дороги. Если же он выехал на тротуар, то должен подготовиться ко встрече с пешеходами.

Краешек дороги, отделенный только нарисованной полосой и отведенный велосипедистам, обозначается знаком «Полоса для велосипедистов»: это вышеописанный квадрат с голубым фоном, изображением велосипеда и стрелок, указывающих направление движения в общем потоке. Конец полосы отмечается таким же знаком, перечеркнутым красной линией.

Велопешеходная зона маркируется соответствующим знаком круглой формы с изображением велосипеда и человечка. Указатель информирует людей на велосипедах и без них об их общем праве пользоваться данной дорожкой, а автомобилистов предупреждает о том, что туда нельзя въезжать.

Штрафы за велодорожку

На вопрос, разрешается ли движение пешеходов по специальной велосипедной дорожке, мы уже ответили выше: только в том случае, если у них нет выбора, отсутствует/ремонтируется тротуар. Как правило, за то, что человек просто прошелся без последствий, к нему не предъявляют претензий – разбирательство начнется в случае ДТП с травмами. Тогда наказания за несанкционированный выход на дорожку не миновать. Штраф варьируется от 800 до 1500 р., к этой сумме прибавляется возможная компенсация ущерба. Такие расходы ожидают и велосипедистов, нарушающих правила.

Особое сомнение у водителей вызывают приоритеты при пересечении проезжей части с велосипедной дорожкой или велопешеходной дорожкой. Тут нужно вспомнить, какой знак вы видели: если круглый или квадратный голубой, то с вашей стороны обязательна уступка, а если треугольный с красной обводкой, то вы вправе ожидать подобного от велосипедистов. Но чтобы оградить себя от неприятностей, лучше всегда быть готовым к уступке: пешеходы и велосипедисты часто не знакомы с ПДД, некоторые не получали водительские права, т.е., их знания никто не проверял с особой тщательностью.

За парковку на велодорожке или велополосе, проезд по ним и создание помех для велосипедистов водителя машины ожидает штраф от 500 до 1500 р. Если же автомобилист спровоцировал ДТП или нанёс травмы, то дело может закончиться лишением прав и тюремным заключением.

Движение вдогонку (формула). Решение задач на движение вдогонку

Движение является способом существования всего, что человек видит вокруг себя. Поэтому задачи на перемещение разных объектов в пространстве являются типичными проблемами, которые предлагается разрешить школьникам. В данной статье подробно рассмотрим движение вдогонку и формулы, которые необходимо знать, чтобы уметь решать задачи такого типа.

Что такое движение?

Перед тем, как переходить к рассмотрению формул движения вдогонку, необходимо разобраться с этим понятием подробнее.

Под движением подразумевают изменение пространственных координат объекта за определенный промежуток времени. Например, автомобиль, который движется по дороге, самолет, который летит в небесах, или кошка, бегущая по траве, — все это примеры движения.

Важно отметить, что рассматриваемый движущийся объект (автомобиль, самолет, кошка) считают безмерным, то есть его размеры не имеют совершенно никакого значения для решения проблемы, поэтому ими пренебрегают. Это своего рода математическая идеализация, или модель. Для подобного объекта существует название: материальная точка.

Движение вдогонку и его особенности

Теперь перейдем к рассмотрению популярных школьных задач на движение вдогонку и формул для него. Под этим видом движения понимают перемещение двух или более объектов в одном направлении, которые отправляются в свой путь из разных пунктов (материальные точки имеют разные начальные координаты) или/и в разное время, но из одного и того же пункта. То есть создается ситуация, при которой одна материальная точка пытается догнать другую (другие), поэтому эти задачи получили такое название.

Согласно определению, особенностями движения вдогонку являются следующие:

Наличие двух и более движущихся объектов. Если двигаться будет только одна материальная точка, то ей «некого» будет догонять.
Прямолинейное перемещение в одном направлении. То есть объекты осуществляют движение вдоль одной и той же траектории и в одном направлении. Движение навстречу друг другу не входит в число рассматриваемых задач.
Пункт отправления играет важную роль. Идея заключается в том, чтобы в момент начала движения объекты были разделены в пространстве. Такое разделение будет иметь место, если они стартуют в одинаковое время, но из разных пунктов или же из одного пункта, но в разное время. Старт двух материальных точек из одного пункта и в одинаковое время к задачам вдогонку не относится, поскольку в этом случае один объект будет постоянно удаляться от другого.

Формулы движения вдогонку

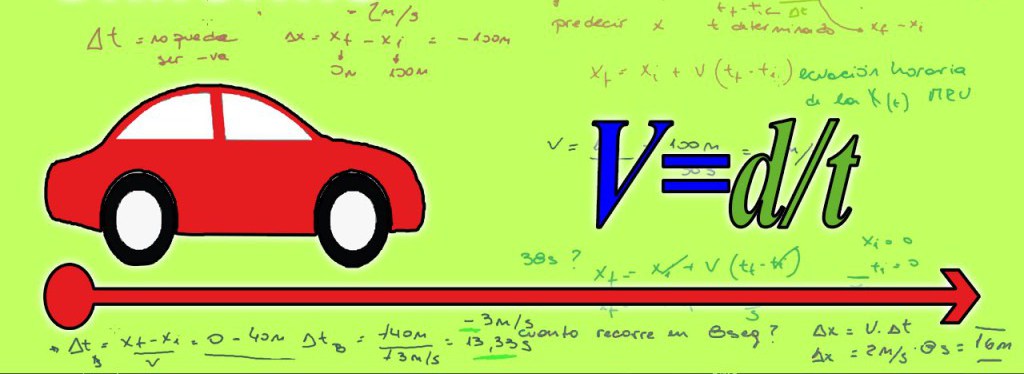
В 4 классе общеобразовательной школы обычно рассматриваются подобные задачи. Это означает, что формулы, которые необходимы для решения, должны быть максимально простыми. Такому случаю удовлетворяет равномерное прямолинейное движение, в котором фигурируют три физических величины: скорость, пройденный путь и время движения:

Скорость — величина, показывающая расстояние, которое проходит тело за единицу времени, то есть она характеризует быстроту изменения координат материальной точки. Обозначается скорость латинской буквой V и измеряется, как правило, в метрах в секунду (м/с) или в километрах в час (км/ч).
Путь — это расстояние, которое проходит тело за время своего движения. Он обозначается буквой S (D) и выражается обычно в метрах или километрах.
Время — период движения материальной точки, который обозначается буквой T и приводится в секундах, минутах или часах.

Описав основные величины, приведем формулы движения вдогонку:

Решение любой задачи рассматриваемого типа базируется на применении этих трех выражений, которые необходимо запомнить каждому школьнику.

Пример решения задачи №1

Приведем пример задачи движения вдогонку и решения (формулы, необходимые для него, приведены выше). Проблема формулируется следующим образом: «Грузовик и легковой автомобиль одновременно выезжают из пунктов A и B со скоростями 60 км/ч и 80 км/ч соответственно. Оба транспортных средства движутся в одном направлении так, что автомобиль приближается к пункту A, а грузовик удаляется от обоих пунктов. Через какое время автомобиль догонит грузовик, если расстояние между A и B составляет 40 км?».

Перед тем как решать задачу, необходимо научить ребят определять суть проблемы. В данном случае она заключается в неизвестном времени, которое проведут оба транспортных средства в пути. Предположим, что это время равно t часам. То есть через время t автомобиль догонит грузовик. Найдем это время.

Рассчитаем расстояние, которое пройдет каждый из движущихся объектов за время t, имеем: s₁ = v₁*t и s₂ = v₂*t, здесь s₁, v₁ = 60 км/ч и s₂, v₂ = 80 км/ч — пройденные пути и скорости движения грузовика и автомобиля до того момента, когда второй догонит первого. Поскольку расстояние между пунктами A и B равно 40 км, то автомобиль, догнав грузовик, пройдет путь на 40 км больше, то есть s₂ — s₁ = 40. Подставляя в последнее выражение формулы для путей s₁ и s₂, получим: v₂*t — v₁*t = 40 или 80*t — 60*t = 40, откуда t = 40/20 = 2 ч.

Отметим, что данный ответ можно получить, если использовать понятие скорости сближения между движущимися объектами. В задаче она равна 20 км/ч (80-60). То есть при этом подходе возникает ситуация, когда один объект движется (автомобиль), а второй относительно него стоит на месте (грузовик). Поэтому достаточно поделить расстояние между пунктами A и B на скорость сближения, чтобы решить задачу.

Пример решения задачи №2

Приведем еще один пример задач на движение вдогонку (формулы для решения используются те же): «Из одного пункта выезжает велосипедист, а через 3 часа в ту же сторону выезжает автомобиль. Через какое время после начала своего движения автомобиль догонит велосипедиста, если известно, что он движется в 4 раза быстрее?».

Решать эту задачу следует так же, как и предыдущую, то есть необходимо определить, какой путь пройдет каждый участник движения до момента, когда один догонит другого. Предположим, что автомобиль догнал велосипедиста через время t, тогда получаем следующие пройденные пути: s₁ = v₁*(t+3) и s₂ = v₂*t, здесь s₁, v₁ и s₂, v₂ — пути и скорости велосипедиста и автомобиля соответственно. Заметим, что до того, как автомобиль догнал велосипедиста, последний находился в пути t + 3 часа, так как он выехал на 3 часа раньше.

Зная, что оба участника отправились из одного пункта, и пройденные ими пути будут равны, получаем: s₂ = s₁ или v₁*(t+3) = v₂*t. Скорости v₁ и v₂ нам не известны, однако в условии задачи сказано, что v₂ = 4*v₁. Подставляя это выражение в формулу для равенства путей, получим: v₁*(t+3) = 4*v₁*t или t+3 = 4*t. Решая последнее, приходим к ответу: t = 3/3 = 1 ч.

Некоторые советы

Формулы движения вдогонку являются простыми, тем не менее школьников в 4 классе важно научить мыслить логически, понимать значение величин, с которыми они имеют дело, и осознавать проблему, которая перед ними стоит. Ребят рекомендуется призывать к рассуждениям вслух, а также к командной работе. Кроме того, для наглядности задач можно использовать компьютер и проектор. Все это способствует развитию у них абстрактного мышления, коммуникативных навыков, а также математических способностей.

Источники:

http://msk.edu.ua/ivk/Fizika/Konspekt/otnositelnost_dvig.php
https://drivertip.ru/osnovy/vsyo-o-znake-velosipednaya-dorozhka.html
https://fb.ru/article/421647/dvijenie-vdogonku-formula-reshenie-zadach-na-dvijenie-vdogonku