Какую линейную скорость имеют верхние точки обода велосипедного колеса 20

КПД велосипеда и в биологическом, и в механическом отношении очень высок. Исследователи подсчитали, что с точки зрения затрат количества энергии, которое человек должен потратить на преодоление заданного расстояния, велосипед является наиболее эффективным самодвижущемся транспортных средств. С механической точки зрения с педалей на колёса передаётся до 99% энергии, хотя использование механизма переключения передач может уменьшить эту величину на 10-15%. С точки зрения соотношения веса полезного груза, который велосипед может везти к общему весу, то велосипед является также наиболее эффективным средством транспортировки грузов.

Энергетическая эффективность

Человек, едущий на велосипеде на низких и средних скоростях (16-24 км/ч), использует такую же мощность, которая требуется для ходьбы, поэтому велосипед является наиболее энергоэффективным общедоступным транспортным средством. Аэродинамическое сопротивление, которое увеличивается приблизительно пропорционально квадрату скорости, требует более высокой мощности относительно скорости из-за того, что с ростом скорости велосипеда требуемая мощность увеличивается в кубической зависимости, так как мощность равна скорости умноженной на силу: P = F * v (рис. 1.). Велосипед, в котором ездок находится в лежачем положении называется лигерад (альтернативное название — рикамбент), а если велосипед имеет аэродинамический обтекатель, используемый для достижения очень низкого аэродинамического сопротивления, то он называется стримлайнер.

Рис. 1. Зависимость требуемой мощности от скорости велосипеда.

На твёрдой, плоской поверхности человеку весом 70 кг требуется энергия около 30 Вт, что бы двигаться со скоростью 5 км/час. Тот же человек на велосипеде, находясь на той же поверхности и расходуя ту же мощность, может двигаться со средней скоростью 15 км/ч, так что расход энергии в кКал/(кг*км) будет примерно в три раза меньше. Обычно используются такие цифры:

1.62 кДж/(км*кг) для езды на велосипеде,
3.78 кДж/(км*кг) для ходьбы/бега,
16.96 кДж/(км*кг) для плавания.

Велогонщики — любители обычно могут развивать мощность 3 Вт/кг в течении более чем часа (например, около 210 Вт для гонщика весом 70 килограммов), лучшие из любителей развивают 5 Вт/кг и элитные спортсмены могут достигать мощности 6 Вт/кг за аналогичные периоды времени. Элитные трековые велогонщики-спринтеры способны кратковременно достигать максимальной мощности около 2000 ватт, или более 25 Вт/кг; элитные шоссейные велогонщики могут кратковременно развивать максимальную мощность от 1600 Вт до 1700 Вт для мгновенного рывка на финишной прямой в конце пятичасовой шоссейной гонки.

Даже при движении на умеренных скоростях большая часть энергии тратится на преодоление аэродинамического сопротивления, которое увеличивается пропорционально квадрату скорости. Таким образом, мощность, необходимая для преодоления сопротивления воздуха возрастает пропорционально кубу скорости.

Типичные велосипедные скорости

Типичные скорости для велосипедов лежат в диапазоне от 15 до 30 км/ч. На быстром гоночном велосипеде, средний гонщик может ехать на скорости 50 км/ч по ровной поверхности в течение коротких отрезков времени. Самая высокая скорость, официально зарегистрированная для транспортного средства, приводимого в действие мускульной энергией при движении по ровной поверхности в безветренную погоду и без внешней помощи (то есть перед транспортным средством не двигалась какая-либо машина или мотоцикл) составила 133,284 км/ч. Этот рекорд был установлен Сэм Уиттингем в 2009 году в Варне. В 1989 году во время гонок через всю Америке группа транспортных средств, приводимых в действие мускульной энергией пересекла Соединённые Штаты всего за 6 дней. Самая высокая скорость, официально зарегистрированная при езде на велосипеде с обычной вертикальной посадкой гонщика при прочих равных условиях составила 82,52 км/ч на дистанции более 200 метров. Этот рекорд был установлен в 1986 году Джимом Гловером на велосипеде модели «Мультон АМ7» на третьем международном научном симпозиуме транспортных средств, приводимых в действие мускульной в Ванкувере.

Вес против мощности

Был проведён крупный конкурс, задачей которого ставилось снижение веса гоночных велосипедов за счёт использования современных материалов и компонентов. Кроме того, в современных колёсах стоят подшипники с низким коэффициентом трения, используются и другие возможности для снижения сопротивления, однако в проведённых испытаниях эти компоненты практически не влияли на характеристики велосипеда во время езды по ровной дороге. Например, снижение веса велосипеда на 0,45 кг даст тот же эффект при соревновании на время на 40 километровой дистанции по ровной дороге, что и удаление какой-либо выступающей части, имеющей площадь аэродинамической поверхности размером с карандаш. Кроме того, международный союз велосипедистов устанавливает ограничение на минимальный вес велосипеда, который будет допущен до участия в гонках, чтобы препятствовать создание настолько тонких конструкций велосипедов, что их использование будет небезопасным. По этой причине при разработке последних моделей велосипедов все усилия были направлены на снижение аэродинамического сопротивления путём применения труб аэродинамической формы, плоских спиц на колёсах, и использования такого руля, что бы положение туловища гонщика и его рук имело бы минимальное аэродинамическое сопротивление. Эти изменения могут существенно повлиять на характеристики, сокращая время прохождения дистанции. Меньший вес приводит к большой экономии времени при езде вверх по склону по холмистой местности.

Кинетическая энергия вращающегося колеса

Рассмотрим кинетическую энергию и «вращающиеся массы» велосипеда для того, чтобы изучить воздействие энергии вращения по сравнению с невращающимися массами.

Кинетическая энергия объекта при поступательном движении определяется по формуле

E=0.5mv 2

Где E — энергия в джоулях, m — масса в килограммах, v — скорость, м/сек. Для вращающихся масс (например, для колеса), кинетическая энергия вращения определяется как

E=0.5Iω 2

Где I — момент инерции, ω — угловая скорость в радианах в секунду. Для колеса со всей его массой, расположенной на внешнем крае (используем это приближение для велосипедного колеса), момент инерции составит

I=0.5mr 2

Где r — радиус в метрах.

Угловая скорость связана с поступательной скоростью и радиусом шины. Если нет скольжения, то угловая скорость будет определятся по формуле:

ω=v/T

когда вращающиеся массы двигаются по дороге, то полная кинетическая энергия равна сумме кинетической энергии поступательного и вращательного движений:

E=0.5mv 2 + 0.5Iω 2

Подставив в предыдущее выражение I и ω, получаем

E = 0.5mv 2 + 0.5mr 2 * v 2 /r 2

Слагаемое r 2 сокращается, и в результате получаем выражение

E = 0.5mv 2 + 0.5mv 2 = mv 2

Другими словами, кинетическая энергия вращающихся масс колёс в два раза больше, чем энергия неподвижных масс велосипеда. Есть доля истины в старой поговорке: «уменьшение веса колёс на фунт равно снижению веса рамы на 2 фунта».

Это все, конечно, зависит от того, насколько точно тонкий обруч является приближённой моделью колеса велосипеда. В действительности же вся масса не может быть сосредоточена в ободе колеса. Для сравнения другой крайностью может быть колесо, масса которого распределена равномерно по всему диску. В этом случае I = 0.5mr 2 , и поэтому полная результирующая кинетическая энергия становится равна E = 0.5mv 2 + 0.25mv 2 = 0.75mv 2 . Уменьшение массы колеса на один килограмм эквивалентно снижению массы рамы велосипеда на 1,5 кг. Параметры большинства колёс реальных велосипедов будут находиться где-то посередине между этими двумя крайностями.

Ещё одним интересным выводом из этого уравнения является то, что для велосипедных колёс, которые не скользят при движении, кинетическая энергия не зависит от их радиуса. Иными словами, преимущество колёс диаметром 650 мм в их низком весе, а не из-за их меньшего диаметра, как это часто утверждается. Кинетическая энергия для других вращающихся масс на велосипеде очень мала по сравнению с кинетической энергией колёс. Например, если вращать педали со скоростью примерно 1/5 от скорости колёс, то их кинетическая энергия составит около 1/25 (на единицу веса) от энергии колёс. Поскольку их центр масс движется по меньшему радиусу, то их энергия ещё больше снижается.

Перевод в килокалории

Предполагая, что вращающееся колесо можно рассматривать как сумму масс обода и шины и плюс ещё 2/3 от массы спиц, все это расположен по центру обода/шин. Для велосипедиста весом 82 кг на велосипеде весом 8 кг, (общий вес составляет 90 кг) при скорости 40 км/ч, кинетическая энергия составит 5625 джоулей для велосипедиста плюс 94 джоуля для вращающихся колёс (весом 1,5 кг — это общий вес ободов, шин и спиц). Преобразовав джоули в килокалории (для этого надо умножить джоули на 0,0002389) получим 1,4 Ккал (это пищевые калории).

Эти 1,4 Ккал являются той энергией, которая необходима для разгона велосипеда с места, или же которая рассеивается в виде тепла при торможении для полной остановки. Этих 1,4 килокалорий хватит для того, что бы нагреть 1 кг воды на 1,4 градуса по Цельсию. Поскольку теплоёмкость алюминия составляет 21% от теплоёмкости воды, то этого количества энергии хватит что бы нагреть колёсные диски весом 800 грамм, сделанные из алюминиевого сплава, на 8° C при быстрой остановке. Обода нагреваются не очень сильно при остановке на ровной дороге. Чтобы рассчитать расход энергии велосипедистом, коэффициент полезного действия принимают за 24%, получится 5,8 ккал, необходимых для разгона велосипеда и гонщика до скорости 40 км/ч, что занимает около 0,5% энергии, необходимой для езды со скоростью 40 км/ч в течение часа. Этот расход энергии будет происходить за 15 секунд, со скоростью примерно 0,4 ккал в секунду, в то время как при устойчивой езде со скоростью 40 км/ч требуется 0,3 килокалорий в секунду.

Преимущества лёгких колёс

Преимущество лёгких велосипедов, и в особенности лёгких колёс относительно кинетической энергии заключается в том, что кинетическая энергия начинает проявлять своё влияние только тогда, когда скорость движения велосипеда изменяется, поэтому есть два случая, когда лёгкие колеса дают преимущество: в спринте и при преодолении крутых поворотов в критериуме.

В спринте на дистанцию 250 м при движении со скоростью от 36 до 47 км/ч, при весе велосипеда и спортсмена 90 кг, плюс ещё 1,75 кг веса колёс (ободы, шины, спицы) кинетическая энергия увеличивается на 6360 джоулей (сжигаются 6,4 ккал). Если снизить общий вес ободов, шин и спиц на 500 г, то эта кинетическая энергия уменьшится на 35 Дж (1 ккал = 1,163 Ватт-час). Влияние этой экономии веса на скорость или пройденное расстояние довольно сложно вычислить, необходимо знать мощность, развиваемую спортсменом и длину спринтерской дистанции. Расчёты показывают, что снижение массы колёс на 500 грамм даст выигрыш для спринтера в во времени 0,16 секунд, и выигрыш в пройденном расстоянии 188 см. Если сделать колёса аэродинамическим, то выигрыш составит 0,05 км/ч при скорости 40 км/ч, польза от снижения веса будет пренебрежительна мала по сравнению с пользой, полученной от аэродинамической формы колёс. Для сравнения, лучшие велосипедные колёса аэродинамической формы дают выигрыш около 0,6 км/ч при скорости 40 км/ч, так что в спринте стоит применить комплект колёс аэродинамической формы весом 500 г и меньше.

В критериуме (групповая кольцевая гонка) гонщик часто начинает резко разгоняться после прохождения каждого поворота. Если велосипедист должен тормозить перед прохождением каждого поворота (а не катиться по инерции, что бы сбросить скорость), то кинетическая энергия, которая добавляется при каждом разгоне, теряется в виде тепла при торможении. При гонке критериум по равнинной местности со скоростью 40 км/ч, с длиной одного круга 1 км и каждый круг имеет 4 поворота, потеря скорости на каждом повороте составляет 10 км/ч. Продолжительность гонки составляет один час, вес гонщика — 80 кг, велосипеда — 6.5 кг, обода, диски и спицы весят 1.75 кг, в этой гонке придётся преодолеть 160 поворотов. На это потребуется дополнительные 387 ккал к 1100 килокалориям, требуемым для езды с постоянной скоростью на той же дистанции. Снижение веса колёс на 500 г снизит общее потребление энергии тела на 4,4 ккал. Если добавление дополнительных 500 г веса в колёса привело к снижению аэродинамического сопротивления на 0,3% (это даёт увеличение скорости на 0,03 км/ч при езде со скоростью 40 км/ч), то расход калорий на компенсацию дополнительного веса будет компенсирован снижением аэродинамического сопротивления.

Ещё одно место, где лёгкие колёса могут иметь большое преимущество, это езда в горку. Можно даже услышать такое выражение, как «эти колеса добавили 0,5-1 км/ч скорости» и т. д. Из формулы для расчёта мощности следует, что 450 грамм сэкономленной массы дадут прибавку 0,1 км/ч к скорости при езде в горку с подъёмом в 4°, и даже сэкономленные 1,8 кг веса дадут прибавку скорости только 0,4 км/ч для лёгкого спортсмена. Итак, из-за чего возникает значительный положительный эффект при снижения веса колёс? Одни предполагают, что нет никакой экономии нет, а действует «эффект плацебо». Так же было предположено, что изменение скорости при каждом нажатии на педали при езде в гору объясняет полученное преимущество. Однако энергия при изменениях скорости сохраняется — во время фазы нажатия педалей велосипед немного ускоряется, при этом кинетическая энергия накапливается, а в «мёртвых зонах» во время прохождения педалями верхней точки хода велосипед замедляется, так что кинетическая энергия восстанавливается. Таким образом, увеличение вращающейся массы может несколько снизить колебания изменений скорости велосипеда, но оно не увеличивает потребность в дополнительной энергии.

Более лёгкие велосипеды легче преодолевают подъёмы, но влияние «вращающейся массы» является проблемой лишь во время быстрого ускорения, но и даже тогда оно мало.

Объяснения

Возможные технические объяснения широко заявленных преимуществ лёгких компонентов в целом, и лёгких колёс в частности, заключается в следующем:

1. Лёгкий вес выигрывает в тех гонках, где имеются значительные подъёмы, потому что более тяжёлые велосипеды не могут компенсировать потерю энергии на спуске или при езде по равнине: гонщик на более лёгком велосипеде просто катится по инерции. Кроме того, если два одинаковых велосипедиста на тяжёлом и лёгком велосипедах одновременно достигают нижней точки после подъёма до финиша, то всё преимущество переходит лёгкому велосипеду. Это не тот случай при соревнованиях в холмистой местности на время (или одиночная езда), где преимущество более тяжелых, но более аэродинамические колёс легко компнсирует расстояние, потерянное на подъемах.
2. Велосипеды с легким весом выигрывают в спринте потому что им легче придать ускорение. Но обратите внимание, что более тяжёлые аэродинамические колеса дают значительные преимущества при увеличении скорости, а на значительной части гонки спринтер немного ускоряется, но в основном тратит все усилия на преодоление аэродинамического сопротивления. Во многих ситуациях в спринте победе могут способствовать более тяжелые, но более аэродинамические колеса.
3. Лёгкий вес даёт преимущество в критериуме в связи с постоянным ускорением после прохождения каждого поворота. Тяжёлые, но более аэродинамические колеса дают небольшое преимущество, так как гонщики находятся в группе большую часть времени. Экономия энергии от лёгких колес минимальна, но она может быть более существенной, так как мышцы ног должны делать дополнительное усилие каждый раз при нажатии на педали.

Есть два «нетехнических» объяснения эффекта легкого веса. Во-первых, это эффект плацебо. Так как велосипедист чувствует, что он находятся на лучшем (лёгком) велосипеде, то он крутит педали сильнее и, следовательно, быстрее едет. Второе, не техническое объяснение заключается в триумфе надежды над опытом велосипедиста — из-за меньшего веса велосипеда его скорость увеличивается несущественно, но велосипедист думает, что он едет быстрее. Иногда это связано с отсутствием реальных данных, например, когда велосипедисту потребовалось два часа, чтобы подняться на холм на своём старом велосипеде, а на новом велосипеде он сделал это за 01:50. Не учитываются такие факторы как соответствие велосипедиста велосипеду в течении этих двух подъёмов, была ли погода жаркая или ветренная, в какую сторону дул ветер, какое было самочувствие у гонщика и т.д.

Другим объяснением, конечно, может быть маркетинговые преимущества, связанные с продвижением идеи снижения веса.

В конце концов аргумент о «возростающем потреблении мускульной энергии» является единственным, который может поддержать заявленные преимущества лёгких колёс в тех ситуациях, где нужен быстрый разгон. Этот аргумент должен был бы утверждать, что если велосипедист находится уже на пределе усилий на каждом рывке или при каждом нажатии педалей, то небольшое количество дополнительной мощности, необходимре для компенсации лишнего веса, будет являться значительной физиологической нагрузкой. Не ясно, верно ли это утверждение но это единственное объяснение заявленных преимуществ от снижения веса колёс (по сравнению со снижением веса остальной части велосипеда). Для этих ускорений, не имеет разницы, стали ли легче колёса на полкилограмма или на килограмм стал легче вес велосипеда и спортсмена. Чудодейственность лёгких колёс (по сравнению с уменьшением веса в любой другой части велосипеда) трудно увидеть.

Равномерное движение тела по окружности

1. Движением тела по окружности называют движение, траекторией которого является окружность. По окружности движутся, например, конец стрелки часов, точки лопасти вращающейся турбины, вращающегося вала двигателя и др.

При движении по окружности направление скорости непрерывно изменяется. При этом модуль скорости тела может изменяться, а может оставаться неизменным. Движение, при котором изменяется только направление скорости, а её модуль сохраняется постоянным, называется равномерным движением тела по окружности. Под телом в данном случае имеют в виду материальную точку.

2. Движение тела по окружности характеризуется определёнными величинами. К ним относятся, прежде всего, период и частота обращения. Период обращения тела по окружности \( T \) — время, в течение которого тело совершает один полный оборот. Единица периода — \( [\,T\,] \) = 1 с.

Частота обращения \( (n) \) — число полных оборотов тела за одну секунду: \( n=N/t \) . Единица частоты обращения — \( [\,n\,] \) = 1 с -1 = 1 Гц (герц). Один герц — это такая частота, при которой тело совершает один оборот за одну секунду.

Связь между частотой и периодом обращения выражается формулой: \( n=1/T \) .

Пусть некоторое тело, движущееся по окружности, за время \( t \) переместилось из точки А в точку В. Радиус, соединяющий центр окружности с точкой А, называют радиусом-вектором. При перемещении тела из точки А в точку В радиус-вектор повернётся на угол \( \varphi \) .

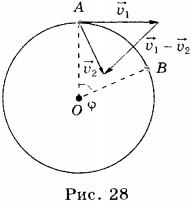
Быстроту обращения тела характеризуют угловая и линейная скорости.

Угловая скорость \( \omega \) — физическая величина, равная отношению угла поворота \( \varphi \) радиуса-вектора к промежутку времени, за которое этот поворот произошел: \( \omega=\varphi/t \) . Единица угловой скорости — радиан в секунду, т.е. \( [\,\omega\,] \) = 1 рад/с. За время, равное периоду обращения, угол поворота радиуса-вектора равен \( 2\pi \) . Поэтому \( \omega=2\pi/T \) .

Линейная скорость тела \( v \) — скорость, с которой тело движется вдоль траектории. Линейная скорость при равномерном движении по окружности постоянна по модулю, меняется по направлению и направлена по касательной к траектории.

Линейная скорость равна отношению пути, пройденному телом вдоль траектории, ко времени, за которое этот путь пройден: \( \vec=l/t \) . За один оборот точка проходит путь, равный длине окружности. Поэтому \( \vec=2\pi\!R/T \) . Связь между линейной и угловой скоростью выражается формулой: \( v=\omega R \) .

Из этого равенства следует, что чем дальше от центра окружности расположена точка вращающегося тела, тем больше её линейная скорость.

4. Ускорение тела равно отношению изменения его скорости ко времени, за которое оно произошло. При движении тела по окружности изменяется направление скорости, следовательно, разность скоростей не равна нулю, т.е. тело движется с ускорением. Оно определяется по формуле: \( \vec=\frac>\) и направлено так же, как вектор изменения скорости. Это ускорение называется центростремительным ускорением.

Центростремительное ускорение при равномерном движении тела по окружности — физическая величина, равная отношению квадрата линейной скорости к радиусу окружности: \( a=\frac \) . Так как \( v=\omega R \) , то \( a=\omega^2R \) .

При движении тела по окружности его центростремительное ускорение постоянно по модулю и направлено к центру окружности.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. При равномерном движении тела по окружности

1) изменяется только модуль его скорости
2) изменяется только направление его скорости
3) изменяются и модуль, и направление его скорости
4) не изменяется ни модуль, ни направление его скорости

2. Линейная скорость точки 1, находящейся на расстоянии \( R_1 \) от центра вращающегося колеса, равна \( v_1 \) . Чему равна скорость \( v_2 \) точки 2, находящейся от центра на расстоянии \( R_2=4R_1 \) ?

1) \( v_2=v_1 \)
2) \( v_2=2v_1 \)
3) \( v_2=0,25v_1 \)
4) \( v_2=4v_1 \)

3. Период обращения точки по окружности можно вычислить по формуле:

1) \( T=2\pi\!Rv \)
2) \( T=2\pi\!R/v \)
3) \( T=2\pi v \)
4) \( T=2\pi/v \)

4. Угловая скорость вращения колеса автомобиля вычисляется по формуле:

1) \( \omega=a^2R \)
2) \( \omega=vR^2 \)
3) \( \omega=vR \)
4) \( \omega=v/R \)

5. Угловая скорость вращения колеса велосипеда увеличилась в 2 раза. Как изменилась линейная скорость точек обода колеса?

1) увеличилась в 2 раза
2) уменьшилась в 2 раза
3) увеличилась в 4 раза
4) не изменилась

6. Линейная скорость точек лопасти винта вертолёта уменьшилась в 4 раза. Как изменилось их центростремительное ускорение?

1) не изменилось
2) уменьшилось в 16 раз
3) уменьшилось в 4 раза
4) уменьшилось в 2 раза

7. Радиус движения тела по окружности увеличили в 3 раза, не меняя его линейную скорость. Как изменилось центростремительное ускорение тела?

1) увеличилось в 9 раз
2) уменьшилось в 9 раз
3) уменьшилось в 3 раза
4) увеличилось в 3 раза

8. Чему равен период обращения коленчатого вала двигателя, если за 3 мин он совершил 600 000 оборотов?

1) 200 000 с
2) 3300 с
3) 3·10 -4 с
4) 5·10 -6 с

9. Чему равна частота вращения точки обода колеса, если период обращения составляет 0,05 с?

1) 0,05 Гц
2) 2 Гц
3) 20 Гц
4) 200 Гц

10. Линейная скорость точки обода велосипедного колеса радиусом 35 см равна 5 м/с. Чему равен период обращения колеса?

1) 14 с
2) 7 с
3) 0,07 с
4) 0,44 с

11. Установите соответствие между физическими величинами в левом столбце и формулами для их вычисления в правом столбце. В таблице под номером физической
величины левого столбца запишите соответствующий номер выбранной вами формулы из правого столбца.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
А) линейная скорость
Б) угловая скорость
В) частота обращения

ФОРМУЛА
1) \( 1/T \)
2) \( v^2/R \)
3) \( v/R \)
4) \( \omega R \)
5) \( 1/n \)

12. Период обращения колеса увеличился. Как изменились угловая и линейная скорости точки обода колеса и её центростремительное ускорение. Установите соответствие между физическими величинами в левом столбце и характером их изменения в правом столбце.
В таблице под номером физической величины левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) угловая скорость
Б) линейная скорость
B) центростремительное ускорение

ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ
1) увеличилась
2) уменьшилась
3) не изменилась

Часть 2

13. Какой путь пройдёт точка обода колеса за 10 с, если частота обращения колеса составляет 8 Гц, а радиус колеса 5 м?

Разрушаем мифы. Заблуждения про колеса велосипеда и карбон

Мифов о велосипедах существует очень много, они устойчиво закрепляются в головах райдеров разными способами.
Какие-то передаются от отца к сыну, какие-то от друзей, какие-то от веломастеров, что-то закрепляется в головах при помощи ярых энтузиастов, создающих массу тем на соответствующих форумах и подкрепляющих те или иные мифы историями сомнительного происхождения — способов их распространения много.
Происходит же это частично из-за технической неграмотности, частично из-за нежелания критически переосмыслить существующие факты. В некоторых случаях эти факты просто игнорируются, так как неудобны, а попытка открыть глаза другому может быть встречена весьма агрессивно.

И всё-таки мы попробуем.

Карбон со временем теряет жесткость.

Этот миф еще не успел прочно поселиться в головах велосипедистов, однако он тоже существует. Давайте разбираться.

В широком доступе карбоновые рамы стали появляться в 90-х годах и. они ездят до сих пор. То же касается и алюминиевых, которым отводят всего пять лет. Стальные рамы, которые должны были десять раз уже сломаться от усталостного разрушения материала и коррозии — тоже ездят. Каким бы материал изготовления велосипеда ни был, всегда найдутся скептики, пророчащие ему скорую кончину.

Тем не менее, как и в других мифах, здесь тоже есть зерно истины.
Смола, которая заполняет пространство между волокнами карбона тоже участвует в формировании жесткости элементов. При повторяющихся изгибах в ней, действительно, накапливаются микротрещины. Тогда вся нагрузка в полном объеме ложится на карбон, чей ресурс в разы выше той же смолы. Разрушения не происходит. Но трещины же накапливаются, а значит и теряется жесткость.

Всё так. Да не так. Инженеры компании Specialized проводили исследования на эту тему и выяснили, что после 100 000 циклов деформации жесткость конструкции падает, её можно измерить точными приборами. Однако величины эти настолько малы, что зафиксировать их можно, как раз-таки только точными приборами, человеку такая чувствительность не под силу.

Кстати, возможно, миф подкрепляется, когда гонщик пересаживается на более свежую карбоновую модель велосипеда. В этом случае да, жесткость старой будет казаться намного ниже на контрасте.
Но если помнить о том, что каждая обновленная модель становится на 10-30% жестче своей предшественницы, из-за новых технологий и применяемых материалов, то все вопросы сразу отпадают.

Вес колес имеет большое значение.

Существует устойчивый стереотип, что снижение веса колес следует проводить в первую очередь, так как это в значительной мере влияет на ускорение и торможение. Вращающийся маховик. чем он легче, тем быстрее ускоряешься. ну, вы знаете.

Костью поперек горла становится исследование инженера Крейга Виллетта в 2001 году. Ему удалось эмпирическим путем выяснить, что в первую очередь на разгон влияет. аэродинамика. Вторым по важности идет вес, да. Впрочем, Крейг считает, что разница в раскручивании тяжелых и легких колес невелика. Она есть, но настолько мала, что ей можно пренебречь.

Я и сам был ярым адептом этого мифа и у меня возникает вопрос — а как же ощущения от ускорения? Я же хорошо чувствовал разницу! На что Крейг дал ответ 19 лет назад — величина ускорения велосипеда незначительна, как незначительна и разница в раскрутке тяжелых или легких колес при таком незначительном ускорении. Мда, жаль расставаться с таким красивым мифом.

Мне вот доводилось скидывать по 200 граммов с каждого МТБ колеса в свое время, и я был в восторге от того, насколько легче становилось ехать. Потом с каждого колеса скинул еще по грамм 800. резина полегче, камеры в мусорку, колеса пушинки. ездить-то становится легче, я же чувствую. А может свою роль сыграло общее снижение веса велосипеда на 5 килограммов. Вот как тут узнать, от чего ездить было легче?) Но опытный инженер всё хорошо измерил и разбивает все мои попытки самообмана просто вдребезги, чего и вам желаю)

В самых быстрых дисциплинах, таких как гонка с раздельным стартом или трек, часто используются тяжелые дисковые колеса

В общем, он нам рекомендует иметь в арсенале аэроколеса вместо легких, от них эффект экономии энергии будет намного заметнее. В этом случае речь идет о шоссейных колесах. Хотя попадались на глаза испытания МТБ велосипеда в обтягивающей велоформе и обычной одежде на скоростном спуске (даунхил). Обтягивающая форма позволила гонщику стать быстрее. Казалось бы, где МТБ и аэродинамика, а даже в этой ситуации воздух оказывает сопротивление. Впрочем, это уже совсем другая история.

Узкие покрышки быстрее.

Всем хорошо известно — чем тоньше и легче детали в шоссейной технике, тем выше эффективность велосипеда и тем он быстрее, так ведь?

Великое множество тестов показали, что увеличение диаметра покрышки с 23 до 25 мм сказывается положительно на эффективности, так как широкая шина имеет меньшее сопротивление качению, если материалы, глубина протектора и корд одинаковы в обоих случаях. Возникает сразу вопрос веса, ведь широкая покрышка тяжелее. Предыдущий миф вспоминаем — значение веса колес преувеличено. Тем более, разница всего в несколько граммов на колесе. Вряд ли ее ощутит гонщик, если только не будет всю дорогу внимательно следить за показаниями точных приборов.

А проследить есть за чем. Заморочились этим вопросом в компании CyclingPowerLab. Фронтальная площадь шоссейного велосипеда в среднем около 0,36 кв.м. Смена 23-й покрышки на 25-ю даёт увеличение на 0,001436 кв.м или на 0,4%. Теперь представим, что на 23-й покрышке вы едите со скоростью 30 км/ч, затрачивается на поддержание скорости 102 Вт. На поддержание такой же скорости на 25-й резине потребуется уже 102,5 Вт. Напомню, что мы говорим только об аэродинамическом сопротивлении. Если же вспомнить про сопротивление качению, то оказывается, что больший (25 мм) диаметр экономит по 0,3 Вт энергии на каждом колесе. Пока все ровно, где же выгода от жирных шин?

Теперь 28 мм. При давлении 6,8 атм они поглощают на 0,5 Вт энергии больше, чем покрышки 23 мм при давлении 8,1 атм. Всего 1 Вт разницы, а какой прирост по комфорту — а вот и выгода.

Получается, что широкие шины — это панацея? Не совсем. Если предстоит спринтерский финиш или скоростная гонка, то узкие покрышки будут побыстрее, так как сопротивление качению с увеличением скорости не изменяется, а вот аэродинамическое сопротивление нарастает. Это всё про гоночный режим.

Для обычного размеренного режима движения широкие покрышки, как ни крути, оказываются намного удобнее. При давлении 5,4 атм 28 мм имеют такое же сопротивление качению, как и 23 мм при давлении 8,1 атм. Здесь возникает вопрос — стоит ли отказываться от комфортного движения в пользу экономии 1 Вт энергии? Ответ прост. Пороговая чувствительность изменения затрачиваемой энергии велосипедиста располагается на уровне 5-10 Вт. Разница в 1 Вт зарегистрируется только чувствительным оборудованием при продувке в аэродинамической трубе на высокой скорости в течении длительного времени.

Да и личный опыт подсказывает, что переход с 23 на 28 мм очень сильно ощущается по комфорту. Вот ничего другого не заметил, кроме увеличения плавности хода на первых же метрах на 28-й покрышке.

Вывод: для повседневного использования широкие покрышки могут оказаться быстрее из-за повышенного комфорта, меньше психической энергии будет затрачиваться на борьбу с дискомфортом, который предполагается при повышенном давлении в покрышке меньшего диаметра. Последние себя хорошо покажут в скоростной гонке или на спринтерском участке, и только там. Разница в затрачиваемой энергии настолько незначительна, что райдером останется незамеченной.

Если с диаметром ясность появилась, но остались вопросы по поводу видов покрышек (трубки, клинчеры, бескамерки), то рекомендуем ознакомиться с нашей статьей на эту тему.

Увлеченный велосипедист с 2014-го года. Терпеть не мог, когда велосипед в ходу издавал посторонние звуки, что заставляло его многократно все перебирать, перемазывать и обновлять. Любит вникать в тонкости, посему многочисленные переборки своего велосипеда вылились в дальнейшем в работу веломехаником. Прошёл тернистый путь от Shimano Acera на Comance Tomahawk через SLX до XTR на Specialized S Works, а потом просто пересел на бюджетный шоссейник на оборудовании Campagnolo Xenon 10. За плечами веломарафон (МТБ) Куяльник 2019-года, где на маршруте Light занял 5-е место. В настоящее время остается активным пользователем велосипеда и продолжает углублять свои знания в этой сфере.

Как расшифровывается маркировка велосипедных шин

При покупке велосипеда нельзя забывать о таком важном требовании к транспортным средствам как надёжность его составных частей. Чтобы грамотно осуществлять подбор и замену покрышек велосипедных колёс, важно, чтобы расшифровка маркировки велосипедных шин не была для владельца велотранспорта тайной за семью печатями.

Размеры камер

Размеры велосипедных камер напрямую зависят от размера колёс, а они, в свою очередь, — от вида велосипеда. Прежде чем выбрать тот или иной показатель для ориентира, необходимо запомнить, что:

колёса с диаметром 16, 18 и 20 мм и выше устанавливаются на детские велосипеды и ВМХ;
колёсами с диаметром ободьев 22 мм и 24 мм оборудуют подростковые байки;
диаметр колёс 26 мм считается идеальным для горных и городских прогулочных велосипедов;
29-дюймовые колёса, как правило, встречаются только на найнерах и на шоссейных велосипедах.

Прежде и теперь

Постичь премудрости современной веломаркеровки не так уж трудно, а вот ещё полстолетия назад разные страны мира никак не могли договориться между собой и привести показатели высоты и ширины велосипедных камер к одному знаменателю. Иногда одинаково маркировали покрышки, которые подходили на одни и те же ободья. К примеру, 26 размеру обода должна была соответствовать камера с 25-тимиллиметровой шириной, по факту имевшей колесо с внешним диаметром 24 7/8. Некоторые производители намеренно указывали чересчур приблизительные размеры, чтобы увеличить число вынужденных продаж, обойти конкурентов. На сегодня вопрос расшифровки числовых кодировок доступен абсолютному большинству велолюбителей.

Европейская маркировка

Покрышки на колёсах большинства современных велосипедов имеют европейскую маркировку, использующую классификацию ETRTO. Эта аббревиатура расшифровывается как European Tire and Rim Technical Organization.

В данной классификации, как правило, используются следующие виды маркировки:

двойная цифровая маркировка велосипедных шин (37-662), где первая цифра соответствует ширине велопокрышки в миллиметрах, а вторая – её диаметру.
тройная цифровая маркировка велосипедных покрышек (28 х 15.8 х 13.8), где указываются примерный внешний диаметр, высота и ширина покрышки соответственно.

Интересно, что на велосипедах советского производства показатели двойной маркировки «переставлены»: сначала значится внутренний диаметр покрышки (он же – посадочный размер ободьев), затем следует ширина камеры.

В настоящее время маркировка, получившая распространение в Европе, признана наиболее чёткой и удобной для применения среди всех существующих. Несмотря на это, во Франции и Великобритании принято маркировать покрышки велосипедных шин по-своему.

Маркировка в дюймах

Эта маркировка, как и предыдущая, состоит из двух значений, записанных через знак умножения или дробь. Если покрышки маркированы, к примеру, как 28 х 1.4, первое число будет соответствовать внешнему диаметру покрышки, а второй – его предполагаемой ширине в дюймах.

У данного вида нанесения маркеров есть существенный недостаток: он имеет приблизительные показатели, что затрудняет подбор велопокрышек с одним и тем же маркером для велосипедов разных видов.

Французская маркировка

Во Франции маркировка может выглядеть вот так: 700 х 35С. Там принято маркировать изделие по внешнему диаметру, ширине и внутреннему диаметру, где 700 – примерный показатель внешнего, а буква – внутреннего диаметра. Чем меньше показатель, тем буква ближе к началу алфавита.

Соответственно, А – самый маленький, а D – самый большой размер. В маркировке представленного образца буква «С» обозначает внешний диаметр в 622 мм. В отличие от других маркировок, французская система записи показателей используется не на всех велосипедах. К примеру, такое обозначение никогда не наносится на горные байки.

Какой посадочный диаметр назвать продавцу?

Подводя итоги и возвращаясь к строгим цифрам, мы должны определиться с тем, какую маркировку назвать продавцу покрышек в вашем конкретном случае.

Для этого нужно в первую очередь определить посадочный диаметр.

У колёс на 27.5 дюймов посадочный диаметр может равняться как 584, так и 590 мм.
26 дюймам соответствуют 559 мм.

А ширина покрышек?

При подборе ширины камер можно пользоваться таблицами соответствия, имеющимися на специализированных технических сайтах или консультациями проверенного продавца. Важно помнить, что предпочтительно выбирать покрышку с шириной, превышающей внутреннюю ширину обода в 1,5-2 раза.

В противном случае могут возникнуть некоторые трудности:

Покрышки, ширина которых многократно превосходит ширину ободьев, затрудняет возможность управления велосипедом на низких скоростях; могут сорваться с обода при внезапном повороте; быстро изнашиваются.
Покрышки с шириной, которая значительно уступает внутренней ширине ободьев, увеличивают риск проколов и механических повреждений обода.

По факту, правильно подобрать размеры и расшифровать маркировку велошин может каждый. Так что держите в голове 2-3 размерных показателя конкретно для вашего байка, чтобы назвать их, как только настанет необходимость заменить камеру. Ну, а если на память вы не надеетесь, сохраните велопокрышку «для образца» и прямо с ней отправляйтесь покупать новую.

Источники:

http://velobajo.ru/bez-rubriki/skorost-vrashheniya-kolesa-velosipeda.html
https://fizi4ka.ru/ogje-2018-po-fizike/ravnomernoe-dvizhenie-tela-po-okruzhnosti.html
https://velojournal.net/razrushaem-mify-zabluzhdeniya-pro-kolesa-velosipeda-i-karbon
https://velofans.ru/vibor/kak-rasshifrovyvaetsya-markirovka-velosipednyh-shin