Задания №11. Задачи на движение по прямой

На этот раз рассматриваем задачи из открытого банка заданий ЕГЭ по математике на прямолинейное движение.
Также смотрите видеолекцию «Текстовые задачи» здесь .
Задачи В14 могут встретиться на ЕГЭ по математике совсем простые, где может даже не потребоваться введение переменной. Чаще будут встречаться задачи, сводимые к решению квадратных уравнений (кстати, что делать, если дискриминант намечается слишком большой, – смотрите здесь и здесь).
Задание 1.
Два велосипедиста одновременно отправились в 130-километровый пробег. Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч.
Пусть км/ч – скорость второго велосипедиста. Тогда согласно условию км/ч – скорость первого велосипедиста.
Оба велосипедиста проехали 130 км.
Третью колонку таблицы заполняем автоматически, пользуясь формулой :
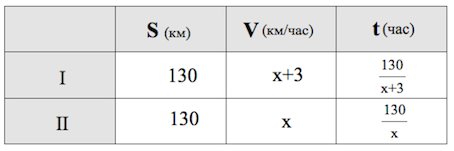
Время движения первого велосипедиста меньше, чем время движения второго на 3 часа, поэтому
Домножаем обе части равенства на , понимая, при этом, что
К финишу придет первым велосипедист со скоростью , поэтому в ответ отправляем величину (км/ч).
Задание 2.
Из пункта А в пункт В, расстояние между которыми 60 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 110 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 5,5 часов позже автомобилиста. Ответ дайте в км/ч.
Задача очень похожа на предыдущую.
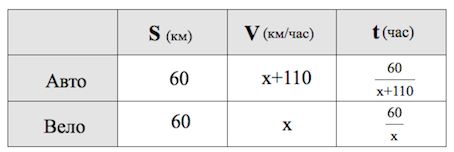
Если не знаете как извлечь корень из большого дискриминанта, загляните сюда и сюда.
Задание 3.
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 80 км. На следующий день он отправился обратно со скоростью на 2 км/ч больше прежней. По дороге он сделал остановку на 2 часа. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
Пусть км/ч – скорость велосипедиста на пути АВ. Тогда согласно условию км/ч – скорость велосипедиста на пути ВА.
Длину пути АВ (ВА) 80 км.
Третью колонку таблицы заполняем автоматически, пользуясь формулой :
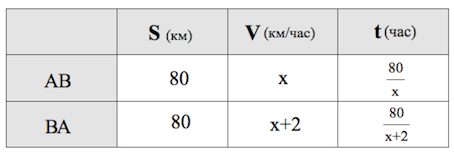
Время движения велосипедиста на пути ВА меньше, чем время движения на пути АВ на 2 часа, поэтому
Откуда вытекает, что (км/ч).
Задание 4.
Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 10 км/ч, а вторую половину пути – со скоростью 60 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 39 км/ч. Ответ дайте в км/ч.
Пусть км/ч – скорость первого автомобиля. Тогда согласно условию км/ч – скорость второго автомобиля на первой половине пути. При этом весь путь считаем км.
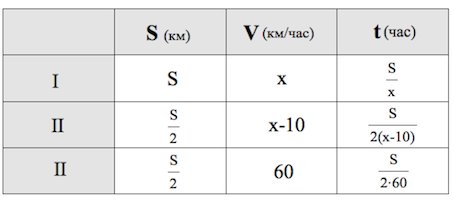
Так как автомобили выехали одновременнно из А и прибыли одновременно в В, то
В условии задачи сказано, что скорость первого автомобиля больше 39 км/ч, поэтому оставляем только вариант
Задание 5.
Из двух городов, расстояние между которыми равно 300 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 70 км/ч и 80 км/ч?
Обозначим за ч время нахождения в пути одного автомобиля до встречи с другим.
Тогда один из автомобилий прошел , второй – км.
В сумме эти пути дают км.
Задание 6.
Из городов A и B, расстояние между которыми равно 300 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 2 часа на расстоянии 160 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч.
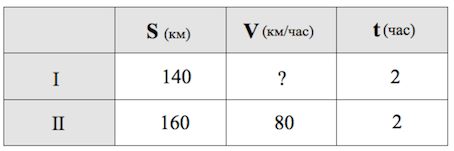
Встреча произошла ближе к А. То есть автомобиль, выехавший из А, проехал меньший путь, нежели автомобиль из В.
Итак, скорость движения автомобиля, выехавшего из А, есть км/ч.
Задание 7.
Расстояние между городами A и B равно 620 км. Из города A в город B выехал первый автомобиль, а через два часа после этого навстречу ему из города B выехал со скоростью 90 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 350 км от города A. Ответ дайте в км/ч.

Второй автомобиль проехал км со скоростью км/ч, значит он находился в пути часа.
Первый автомобиль находился в пути на два часа больше, то есть 5 часов.
Поэтому скорость первого автомобиля, проехавшего км за 5 часов есть км/ч.
Задание 8.
Товарный поезд каждую минуту проезжает на 450 метров меньше, чем скорый, и на путь в 240 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
Прежде всего, переведем м/мин в км/ч.
Обозначаем за км/ч скорость скорого поезда. Тогда скорость товарного – км/ч.
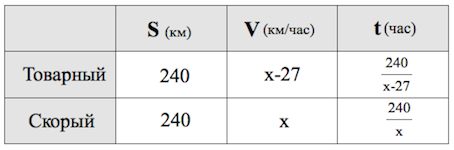
(«Страшные дискриминанты» мы обсуждали здесь)
Откуда Тогда скорость товарного поезда км/ч.
Задание 9.
Расстояние между городами A и B равно 198 км. Из города A в город B выехал автомобиль, а через 3 часа следом за ним со скоростью 80 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.
Пусть расстояние от A до C – км. Так как скорость мотоциклиста км/ч, то время в пути AC мотоциклиста – . По условию сказано, что автомобиль в пути AC находился на 3 часа больше, поэтому указываем в таблице время нахождения автомобиля в пути AC – часов.
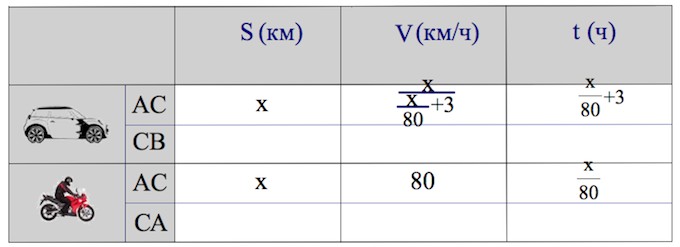
Далее, автомобиль проделывает путь CB, длина которого выражается у нас через , а мотоциклист возвращается обратно, то есть проделывает все тот же путь CA с той же скоростью км/ч за тоже время .
Скорость автомобилиста на пути CB, также как и скорость на пути AC, есть или км/ч.
Поэтому расстояние с этой скоростью он пройдет за время часов.
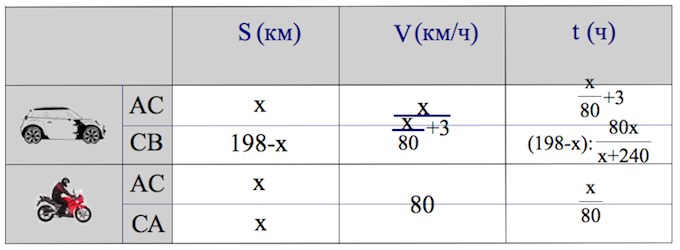
Время прохождения автомобилистом пути CB равно времени прохождения пути CA мотоциклистом, поэтому
Вычисление корня квадратного из большого числа – смотрите здесь.
Задание 10.
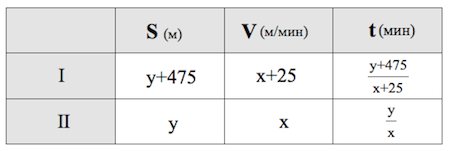
Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 475 метрам?
Обозначаем за м/мин скорость второго пешехода и за м – пройденный им путь.
Задание 11.
Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 12 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.
Обозначим за (км/ч) скорость третьего велосипедиста.
Обозначим за (ч) время, прошедшее от старта третьего велосипедиста до встречи со вторым. За это время третий велосипедист проехал км.
Тогда второй находился в пути до встречи с третьим велосипедистом часов и преодолел путь км.
Далее, первый велосипедист, согласно условию, находился в пути часов до встречи второго и третьего велосипедистов и его путь за это время составил
После этого первый, так же как и третий, проехали еще по и км соответственно.
Нам предстоит решить систему:
Конечно же, второй вариант не подходит, так как скорость третьего велосипедиста явно должна быть больше 12 км/ч, иначе он никого не сможет перегнать.
Задание 12.
Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо придорожного столба за 30 секунд. Найдите длину поезда в метрах.
Согласно условию за 30 секунд поезд проходит расстояние, равное своей длине .
Чтобы найти длину поезда , нужно скорость поезда умножить на секунд.
При этом, заметьте, требуется перевод всех данных в один формат.
Задание 13.
Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо лесополосы, длина которой равна 500 метров, за 36 секунд. Найдите длину поезда в метрах.
Согласно условию за 36 минут поезд проходит м, где – длина поезда.
Переведем км/ч в м/мин:
Задание 14.
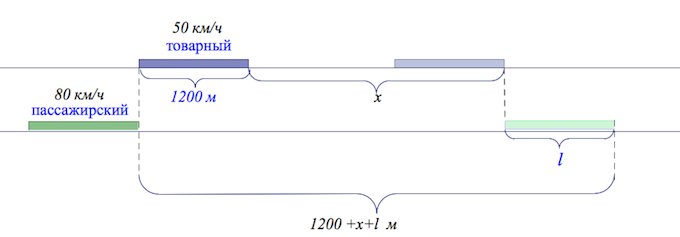
По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 80 км/ч и 50 км/ч. Длина товарного поезда равна 1200 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 3 минутам. Ответ дайте в метрах.
Переведем сразу км/ч в м/мин:
За 3 минуты товарный поезд прошел м:
а пассажирский (м).
Согласно условию пассажирский поезд за 3 минуты прошел путь, равный м.
Смотрите фрагмент видеолекции

Побольше оптимизма! И все будет хорошо!

Вы можете пройти тест по задачам на движение по прямой.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
- Задания №11. Задачи на движение по окружности
- Задания №11. Задачи на смеси и сплавы и т.п.
- Задания №11. Задачи на работу
- Тест по Задачам №11. Задачи на движение
- Задачи №10, часть 1
- Задания №11. Задачи на прогрессию
Здравствуйте! В задании 3 у Вас неправильно найдены корни. Ответ должен быть 8.
ГДЗ Математика 3 класс учебник 3 часть Петерсон. Решебник с ответами ✔
 УМК «Школа 2000» и линейка учебников для программы «Перспектива» — математика третий класс автора Петерсон. На этой странице готовые домашние задания к третьей и заключительной в этом учебном году части учебника.
УМК «Школа 2000» и линейка учебников для программы «Перспектива» — математика третий класс автора Петерсон. На этой странице готовые домашние задания к третьей и заключительной в этом учебном году части учебника.
Начнем новый учебник с решения задач на движение, разберем совершенно разные задачи на эту тему, опережая все другие учебники, в которых задачи на движение разбираются годом позже. Продолжим тренироваться в решении уравнений, так же вперед всех остальных учебников. Ребята, которые учатся по Петерсон, попрактикуются не только хорошо решать уравнения уже в третьем классе, что пригодится на уроках математики до самых старших классов, но и научатся логически мыслить, о чем мы неоднократно писали в анонсах к учебникам Петерсон.
А если у детей и родителей возникли проблемы с домашним заданием по математике, 7 гуру к вашим услугам. У нас в решебнике вы можете посмотреть правильные ответы, а если что-то не понятно, спросить в комментариях, мы постараемся разьяснить.
Пишите, какую страницу сейчас проходите.
Ответы к учебнику математики Петерсон 3 класс 3 часть:
Кликайте по номерам страниц, чтобы выбрать нужную.
 УМК «Школа 2000» и линейка учебников для программы «Перспектива» — математика третий класс автора Петерсон. На этой странице готовые домашние задания к третьей и заключительной в этом учебном году части учебника.
УМК «Школа 2000» и линейка учебников для программы «Перспектива» — математика третий класс автора Петерсон. На этой странице готовые домашние задания к третьей и заключительной в этом учебном году части учебника.
Начнем новый учебник с решения задач на движение, разберем совершенно разные задачи на эту тему, опережая все другие учебники, в которых задачи на движение разбираются годом позже. Продолжим тренироваться в решении уравнений, так же вперед всех остальных учебников. Ребята, которые учатся по Петерсон, попрактикуются не только хорошо решать уравнения уже в третьем классе, что пригодится на уроках математики до самых старших классов, но и научатся логически мыслить, о чем мы неоднократно писали в анонсах к учебникам Петерсон.
А если у детей и родителей возникли проблемы с домашним заданием по математике, 7 гуру к вашим услугам. У нас в решебнике вы можете посмотреть правильные ответы, а если что-то не понятно, спросить в комментариях, мы постараемся разьяснить.
Пишите, какую страницу сейчас проходите.
Ответы к учебнику математики Петерсон 3 класс 3 часть:
Кликайте по номерам страниц, чтобы выбрать нужную.
Страница 3
1. Миша прошёл на лыжах расстояние 80 м за 20 с, а Игорь – 45 м за 15 с. Кто из них прошёл большее расстояние, а кто – меньшее?
Большее расстояние прошел Миша 80 > 45
Кто шёл больше времени, а кто – меньше?
Кто шёл быстрее, а кто – медленнее?
80 : 20 = 4 м/с шел Миша
45 :15 = 3 м/с шел Игорь.
Миша шел быстрее 4 > 3.
Какие величины характеризуют движение объектов?
2. Объясни смысл предложений:
а) Самолёт летит со скоростью 800 км/ч.
Самолет пролетает за час 800 км.
б) Скорость теплохода 45 км/ч.
Теплоход проплывает за час 45 км.
в) Человек идёт со скоростью 4 км/ч.
Человек проходит за час 4 км.
г) Земля движется по орбите со скоростью 30 км/с.
Земля пролетает по орбите 30 км в секунду.
д) Черепаха ползёт со скоростью 4 м/мин.
Черепаха за минуту проползает 4 метра.
Страница 4
а) Скорость космического корабля, если он пролетел 56 км за 8 с.
б) Скорость плота на реке, если он за 4 ч проплыл 16 км.
в) Скорость автобуса, если он прошёл 120 км за 3 ч.
г) Скорость велосипедиста, если он проехал 36 км за 2 ч.
4. Найди карточки, на которых указана скорость:
а) самолёта; б) поезда; в) автомобиля; г) пешехода; д) велосипедиста; е) ракеты. 6 км/с
а) самолёта — 900 км/ч
б) поезда — 60 км/ч
в) автомобиля — 90 км/ч
г) пешехода — 5 км/ч
д) велосипедиста — 20 км/ч
е) ракеты — 6 км/с
Сделай по желанию рисунок и подпиши значение скорости.
5. а) Поезд прошёл 224 км за 4 часа. Его скорость в 3 раза меньше скорости вертолёта. Чему равна скорость вертолёта?
1) 224 : 4 = 56 (км/ч) — скорость поезда.
2) 56 * 3 = 168 (км/ч) — скорость вертолета.
Ответ: 168 км/ч.
б) Плот проплыл 27 км за 9 ч, а моторная лодка – 24 км за 2 ч. Чья скорость больше и на сколько?
1) 27 : 9 = 3 (км/ч) — скорость плота.
2) 24 : 2 = 12 (км/ч) — скорость моторной лодки.
3) 12 — 3 = 9 (км) — на столько скорость моторной лодки больше плота.
Ответ: на 9 км/ч.
6. а) Грузовая машина за 8 ч прошла 280 км, а легковая машина это же расстояние – за 4 ч. Во сколько раз скорость грузовой машины меньше скорости легковой?
1) 280 : 8=35 (км/ч) — скорость грузовой машины
2) 280 : 4=70 (км/ч) — скорость легковой машины
3) 70 : 35=2 (р.) — скорость грузовой машины во столько меньше
Ответ: в 2 раза.
б) Велосипедист за 3 ч проехал 57 км, а мотоциклист за 2 ч проехал на 71 км больше. На сколько километров в час скорость велосипедиста меньше скорости мотоциклиста?
1) 57 : 3 = 19 (км/ч) — скорость велосипедиста.
2) 57 + 71 = 128 (км) — проехал мотоциклист.
3)128 : 2 = 64 (км/ч) — скорость мотоциклиста.
4) 64 — 19 = 45 (км/ч) — на столько скорость велосипедиста меньше скорости мотоциклиста.
Ответ: на 45 км/ч.
7. Реши уравнения с комментированием и сделай проверку:
а) (40 • x) : 10 = 28
40 * х = 28 * 10
х = 280 : 40
х = 7
Проверка:
(40 * 7) : 10 28
б) y : 9 – 28 = 32
у : 9 = 32 + 28
у = 60 * 9
у = 540
Проверка:
540 : 9 – 28 = 32
в) 39 + 490 : k = 46
490 : к = 46 — 39
490 : к = 7
к = 490 : 7
к = 70
Проверка:
39 + 490 : 7 = 46
8. Выполни действия и сделай проверку:
а) 547 923 + 83 699 221 = 84 247 144
Проверка:
84 247 144 — 547 923 = 83 699 221
б) 4 758 036 – 50 854 = 4 707 182
Проверка:
4 707 182 + 50 854 = 4 758 036
в) 90 560 • 200 = 18 112 000
Проверка:
18 112 000 : 200 = 90 560
г) 3 027 600 : 6 = 504 600
Проверка:
504 600 * 6 = 3 027 600
9. По двору ходили гуси. Всего у них было 22 ноги. Подошли 3 утёнка и 4 козлёнка. Сколько ног гуляет теперь по двору?
1) 3 * 2 = 6 (ног) − у утят;
2) 4 * 4 = 16 (ног) − у козлят;
3) 22 + 6 + 16 = 28 + 16 = 44 (ноги) − гуляет по двору.
Ответ: 44 ноги.
Страница 5
1. Прочитай формулы. Что они означают? Какие ещё формулы ты знаешь?
S = a • b — формула для вычисления площади
P = (a + b) • 2 — формула для вычисления периметра
V = a • b • c — формула для вычисления объема
a = b • c + r
Зачем нужны формулы и как их устанавливают?
Формулы нужны для вычисления значений.
2. Аэросани едут со скоростью v = 45 км/ч. Построй в тетради числовой луч и покажи на нём движение саней*.
Какое расстояние преодолеют аэросани за 1 ч, 2 ч, 3 ч, 4 ч, t ч?
Составь и заполни в тетради таблицу. Напиши формулу, выражающую зависимость пройденного расстояния s от времени t.
| Время, t | 1 | 2 | 3 | 4 | t |
| Расстояние , s | 45 | 90 | 135 | 180 | 45*t |
3. Проанализируй решение предыдущей задачи. Установи, как найти расстояние s, пройденное объектом, если он двигался со скоростью v в течение времени t.
Из формулы пути по правилу нахождения неизвестного множителя следует, что:
v = s : t t = s : v
Скорость равна расстоянию, делённому на время движения.• Время движения равно расстоянию, делённому на скорость.
Страница 6
4. Найди неизвестные значения величин по формуле пути s = v • t:
| s | v | t |
| 45 м | 5 м/с | 9 с |
| 48 км | 8 км/ч | 6 ч |
| 21 м | 7 м/мин | 3 мин |
| s | v | t |
| 320 км | 4 км/ч | 80 ч |
| 810 м | 9 м/мин | 90 мин |
| 3000 м | 60 м/с | 50 с |
5. Реши задачи по формуле пути s = v • t:
а) Всадник едет со скоростью 8 км/ч. Какое расстояние он проедет за 4 часа?
1) 8 * 4 = 32 (км) — всадник проедет за 4 часа.
Ответ: 32 км.
б) Чему равна скорость почтового голубя, если за 2 ч он пролетает 120 км?
1) 120 : 2 = 60 (км/ч) — скорость почтового голубя.
Ответ: 60 км/ч
в) Пчела летит со скоростью 6 м/с. За какое время она долетит до улья, если находится на расстоянии 360 м от него?
1) 360 : 6 = 60 (с) — надо пчеле, чтобы пчела долетела до улья
Ответ: 60 секунд.
6. Между городом и деревней 250 км. Машина выехала из города в 10 часов утра и прибыла в деревню в 3 часа дня. С какой скоростью она ехала?
1) 15 — 10 = 5 (ч) — ехала машина.
2) 250 : 5 = 50 (км/ч) — с такой скоростью ехала машина.
Ответ: 50 км/ч.
7. Аквариум имеет форму прямоугольного параллелепипеда. Длина аквариума – 50 см, ширина – 35 см, а высота – 40 см. Его боковые стенки стеклянные. Определи площадь поверхности стекла и объём аквариума.
1) 50 * 35 * 40 = 70 000 (см 3 ) — объем аквариума.
2) 50 * 40 * 2 + 35 * 40 * 2 + 35 * 50 = 2000 * 2 + 1400 * 2 + 1750 = 4000 + 2800 + 1750 = 8 550 (см 2 ) — площадь стеклянных стенок аквариума.
Ответ: 8 550 см 2 площадь стенок и 70 000 см 3 объем аквариума.
8. Реши уравнения с комментированием и сделай проверку:
б) 400 : b – 32 = 48
400 : b = 32 + 48
b = 400 : 80
b = 5
в) 250 + 9 • c = 520
9 * с = 520 — 250
с = 270 : 9
с = 30
9. Запиши множество делителей и множество кратных числа 11 *.
10. Составь программу действий и вычисли:
1 3 5 4 2
а) (63 200 856 – 4 916 321) : 1 + 8 006 512 • (36 – 36) = 58 284 535
1) 63 200 856 – 4 916 321 = 58 284 535
2) 36 — 36 = 0
3) 58 284 535 : 1 = 58 284 535
4) 8 006 512 * 0 = 0
5) 58 284 535 + 0 = 58 284 535
2 4 3 1
б) 1 • 7 007 503 – 29 867 • (387 915 : 387 915) = 6 977 636
1) 387 915 : 387 915 = 1
2) 1 • 7 007 503 = 7 007 503
3) 29 867 • 1 = 29 867
4) 7 007 503 — 29 867 = 6 977 636
11. а) Сколько полных недель в високосном году? Сколько ещё остаётся дней?
366 : 7 = 52 (ост.2) − значит 52 полных недель в високосном году и 2 дня останется;
А в простом году?
365 : 7 = 52 (ост.1) − значит 52 полных недель в простом году и 1 день останется.
б) В году 365 дней, из них 53 вторника. Какой день недели был 1 января этого года?
Так как в году 52 недели, а в обычном году 52 недели и 1 день, значит 1 января был вторником. Иначе в году не могло бы быть 53 вторника.
Ответ: вторник.
Страница 7
1. Назови величины, характеризующие движение объектов. Объясни смысл предложений:
а) Скорость воробья примерно 40 км/ч.
Воробей пролетает 40 км за 1 час
б) Самая быстрая в мире птица сапсан способна развивать скорость до 200 км/ч.
Сапсан может летать со скоростью 200 км в час
в) Африканский страус не может летать, зато разгоняется до 72 км/ч.
Страус может бегать со скоростью 72 км в час
г) Меч-рыба плывёт со скоростью 100 км/ч.
Меч — рыба проплывает 100 км в час
2. Используя формулу пути s = v • t, найди неизвестные значения величин:
| s | v | t |
| 60 км | 20 км/ч | 3 ч |
| 360 м | 9 м/мин | 40 мин |
| 75 дм | 3 дм/с | 25 с |
| s | v | t |
| 48 м | 2 м/мин | 24 мин |
| 540 дм | 30 дм/с | 18 с |
| 256 км | 64 км/ч | 4 ч |
3. По реке плывёт плот со скоростью v = 2 км/ч. Построй в тетради числовой луч и покажи на нём движение плота.
Какое расстояние пройдёт плот за 1 ч, 3 ч, 5 ч, 7 ч, t ч? Составь и заполни в тетради таблицу. Напиши формулу, выражающую зависимость пройденного расстояния s от времени t.
| Время, t | 1 | 3 | 5 | 7 | t |
| Расстояние , s | 2 | 6 | 10 | 14 | 2 * t |
4. а) Космический корабль летит со скоростью 9 км/с. За какое время он пролетит 441 км?
441 : 9 = 49 (с) — за это время пролетит 441 км.
Ответ: 49 с.
б) Сколько метров проплывёт окунь за 8 мин, если будет плыть со скоростью 80 м/мин?
80 * 8 = 640 (м) — проплывет окунь.
Ответ: 640 метров.
в) Подводная лодка проплыла 228 км за 6 ч. Чему равна её скорость?
228 : 6 = 38 (км/ч) — скорость подводной лодки.
Ответ: 38 км.
г) Улитка ползёт со скоростью 5 м/ч. За какое время она проползёт 35 м?
35 : 5 = 7 (ч) — улитка проползет 35 м
Ответ: 7 часов.
Страница 8
5. Составь программу действий и вычисли:
7 1 5 2 8 6 4 3
а) 50 – (600 • 3) : (4 • 25) – 5 • (40 – 7 • 5) = 7
1) 600 • 3 = 1800
2) 4 • 25 = 100
3) 7 * 5 = 35
4) 40 — 35 = 5
5) 1800 : 100 = 18
6) 5 * 5 = 25
7) 50 — 18 = 32
8) 32 — 25 = 7
1 3 2 7 9 4 6 5 8
б) (80 • 8 + 420 : 7) : 100 + (140 : 20 + 38 : 19) • 3 = 34
1) 80 • 8 = 640
2) 420 : 7 = 60
3) 640 + 60 = 700
4) 140 : 20 = 7
5) 38 : 19 = 2
6) 7 + 2 = 9
7) 700 : 100 = 7
8) 9 * 3 = 27
9) 7 + 27 = 34
6. Определи по спидометру скорость движения каждой машины:
легковой автомобиль 100 км/ч
автобус 90 км/ч
грузовик 50 км/ч
7. Придумай задачу, в которой надо найти скорость по известному расстоянию и времени, и реши её
Самолет пролетел 1420 км за 2 часа. С какой скоростью летел самолет?
Решение:
1420 : 2 = 710 (км/ч) скорость самолета.
Ответ: 710 км/ч
5 ч 6 мин > 56 мин
108 мин > 1 ч 8 мин
9 мин 20 с = 560 с
734 с > 7 мин 34 с
1 сут. 15 ч < 115 ч
206 ч > 2 сут. 6 ч
9. Реши уравнения с комментированием и сделай проверку:
а) (780 – m • 60) : 6 = 70
780 – m • 60 = 70 * 60
m * 60 = 780 — 420
m = 360 : 60
m = 6
б) 640 : (x • 9 + 8) = 8
x • 9 + 8 = 640 : 8
x * 9 = 80 — 8
x = 72 : 9
х = 8
10. Запиши множество делителей и множество кратных числа 12.
11. По диаграмме Эйлера–Венна определи, из каких элементов состоят множества A и B. Запиши эти множества с помощью фигурных скобок. Найди их пересечение и объединение.
12. Летела стая гусей, а навстречу им гусак.
– Здравствуйте, 20 гусей!
– Нет, нас не 20. Если б нас было в 2 раза больше, да ещё 3 гуся, да ещё ты с нами, тогда нас было бы 20. Сколько было гусей?
Составим уравнение.
x * 2 + 3 + 1 = 20
x * 2 + 4 = 20
x * 2 = 20 — 4
x * 2 = 16
x = 8
Ответ: 8 гусей.
Страница 9
1. а) Из Москвы в Селижарово выехал автобус со скоростью 60 км/ч. Построй числовой луч и покажи на нём движение автобуса.
Какое расстояние прошёл автобус за 1 ч, 2 ч, 3 ч, 4 ч, 5 ч, 6 ч, t ч?
Через какое время он приедет в Селижарово? Составь и заполни таблицу. Напиши формулу зависимости пройденного расстояния s от времени t.
| Время, t | 1 | 2 | 3 | 4 | 5 | 6 | t |
| Расстояние , s | 60 | 120 | 180 | 240 | 300 | 360 | 60*t |
б) Проанализируй решение предыдущей задачи. Объясни, как можно построить формулу зависимости одной величины от другой.
2. Расстояние между двумя городами 180 км. С какой скоростью надо ехать, чтобы преодолеть это рас-стояние за 1 ч, 2 ч, 3 ч, 4 ч, t ч? Построй формулу зависимости скорости движения v от времени t.
v = 180 : t Все значения для этой формулы приведены в таблице.
| Время, t | 1 | 2 | 3 | 4 | t |
| Скорость, v | 180 | 90 | 60 | 45 | v = 180 : t |
Страница 10
3. Какое расстояние пройдёт поезд за 5 ч, если движется со скоростью 70 км/ч, 82 км/ч, 90 км/ч, 100 км/ч, v км/ч? Составь формулу зависимости расстояния s от скорости v.
Результаты можно записать в таблице
| Время, t | 5 | 5 | 5 | 5 | t = s/v |
| Скорость, v | 70 | 82 | 90 | 100 | v = s/t |
| Путь, S | 350 | 410 | 450 | 500 | s = v * t |
4. Сколько времени потребуется велосипедисту, чтобы проехать 60 км, если скорость его движения 10 км/ч, 12 км/ч, 15 км/ч, 20 км/ч, v км/ч? Составь формулу зависимости времени t от скорости v.
Результаты можно записать в таблице
| Время, t | 6 | 5 | 4 | 3 | t = s/v |
| Скорость, v | 10 | 12 | 15 | 20 | v = s/t |
| Путь, S | 60 | 60 | 60 | 60 | s = v * t |
5. а) Расстояние между двумя пристанями 160 км. Может ли катер пройти это расстояние за 9 ч, если будет идти со скоростью 18 км/ч?
18 * 9 = 162 (км) — пройдет катер за 9 часов.
162 > 160 — да сможет пройти 160 км за 9 часов.
Ответ: сможет.
б) От Сашиного дома до школы 1 км. Успеет ли он прийти в школу за 15 мин, если будет идти со скоростью 80 м/мин?
15 * 80 = 1200 (м) — пройдет Саша за 15 минут.
1200 > 1000
Ответ: сможет.
6. Реши уравнения с комментированием и сделай проверку:
а) 14 – 360 : x = 8
360 : х = 14 — 8
х = 360 : 6
х = 60
Проверка:
14 – 360 : 60 = 8
8 = 8
б) (450 : y + 50) : 70 = 2
450 : y + 50 = 140
450 : y = 90
у = 450 : 90
у = 5
Проверка:
(450 : 5 + 50) : 70 = 2
2 = 2
в) (3 • z + 160) : 7 = 40
3 • z + 160 = 40 * 7
3 • z = 280 — 160
3 • z = 120
z = 40
Проверка:
(3 • 40 + 160) : 7 = 40
40 = 40
7. Запиши множество делителей и множество кратных числа 13.
8. Найди пропущенные цифры. Проверь с помощью калькулятора.
Сделай проверку, выполнив обратные действия.
х 63590
800
50872000
9. Кате надо было разделить число 48 236 на 8. У неё получилось частное 629 и остаток 2. Проверь её вычисления с помощью формулы деления с остатком. Найди ошибку и выполни деление правильно.
Проверка: 8 * 6029 + 4 = 48 236
10. Найди частное и остаток при делении:
а) числа 14 на число 5;
б) числа 6 на число 3;
в) числа 2 на число 3. Обоснуй свой ответ, пользуясь формулой деления с остатком.
11. Выполни действия и сделай проверку:
а) 483 567 823 + 998 430 в) 37 090 • 6000
б) 2 666 990 000 – 89 607 787 г) 210 040 000 : 500
в)
х37090
6000
222540000
б)
_2666990000
89607787
2577382213
г) 210 040 000 : 500 = 2100400 : 5 = 420 080
12. Что дольше длится:
а) 1 сутки или 1000 минут;
60 * 24 = 1440 (мин.) в сутках
дольше длятся 1 сутки
б) 1 месяц или 1000 часов;
24 *30 = 720 (ч.) длится месяц в часах
дольше 1000 часов, чем 1 месяц
в) 1 000 000 секунд или 1 год?
60*60*24*365 = 31 536 000 секунд в году
дольше 1 год
Страница 11
1. а) На числовом луче показано движение велосипедиста. Объясни, откуда он выехал. Куда и с какой скоростью он едет? В какой точке числового луча он был через 1 ч, 2 ч, 3 ч, 4 ч? Сколько времени он затратил на весь путь?
Выехал из населенного пункта Петушки. Едет со скоростью 15 км/ч. Черех час — отметка 60 км, через 2 часа — 45 км, через 3 часа — 30 км, через 4 часа — 15 км. На весь путь от затратил 6 часов до Ромашково.
б) Пусть s – путь, который проехал велосипедист, d – его расстояние до Ромашково и D – расстояние до Горок. Как изменяются d и D в зависимости от времени t – уменьшаются или увеличиваются?
D — увеличивается, d — уменьшается.
в) Заполни таблицу. Запиши формулу зависимости каждой из величин s, d, D от времени движения t.
| Время, t | 0 | 1 | 2 | 3 | 4 | 5 | t |
| Расстояние , s | 0 | 15 | 30 | 45 | 60 | 75 | s=15*t |
| d, км | 75 | 60 | 45 | 30 | 15 | 0 | d = 75 — 15*t |
| D, км | 75 | 90 | 105 | 120 | 135 | 150 | D = 75 + 15*t |
2. а) Определи по рисунку, откуда вышел турист, куда и с какой скоростью он идёт. Построй в тетради числовой луч и покажи на нём движение туриста.
Вышел с Турбазы и идет в населенный пункт Икша. Идет со скоростью 3 км/ч. Построй луч в тетради как в учебнике.
б) Пусть s км – путь, пройденный туристом, d км – расстояние между туристом и Москвой, D км – расстояние до Икши. Заполни таблицу. Запиши формулу зависимости каждой из величин s, d, D от времени движения t.
| Время, t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | t |
| Расстояние , s | 0 | 3 | 6 | 9 | 12 | 15 | 18 | s = 3 * t |
| d, км | 12 | 15 | 18 | 21 | 24 | 27 | 30 | d = 12 + 3 * t |
| D, км | 18 | 15 | 12 | 9 | 6 | 3 | 0 | D = 12 — 3 * t |
Страница 12
3. Расстояние от деревни до станции 40 км. Всадник едет из деревни на станцию со скоростью 14 км/ч. Успеет ли он доскакать до станции за 3 часа?
3 * 14 = 42 (км) — может проехать всадник за 3 часа.
42 > 40
Ответ: сможет.
4. Туристы решили пройти за день 30 км. Они уже прошли 3 ч со скоростью 6 км/ч. Какое расстояние им осталось пройти? За какое время они пройдут это расстояние, двигаясь с прежней скоростью?
1) 3 * 6 = 18 (км) — прошли туристы.
2) 30 — 18 = 12 (км) — осталось пройти.
3) 12 : 6 = 2 (ч) — еще надо туристам.
Ответ: Осталось пройти 12 км. пройдут за 2 часа.
а) Маша прошла n км. Чему равна её скорость, если она затратила на путь k часов?
б) Лена шла a ч со скоростью b км/ч. Какое расстояние она прошла за это время?
в) Витя пробежал x метров за 5 мин, а Саша – за 6 мин. У кого из них скорость больше и на сколько?
У Саши скорость больше на столько м/мин
(x : 5) — (x : 6)
6. Какие свойства сложения и вычитания выражают данные равенства? Объясни их смысл, используя графические модели.
1) a – (b + c) = (a – b) – c = (a – c) – b
2) (a + b) – c = (a – c) + b = a + (b – c)
7. Вычисли наиболее удобным способом:
а) 894 – (294 + 80) = (894 — 294) + 80 = 600 + 80 = 680
б) 715 – 99 – 101 = 715 — (99 + 101) = 515
в) (586 + 245) – 486 = (586 — 486) + 245 = 345
г) (324 + 498) – 298 = 324 + (498 — 298) = 524
д) 232 – (95 + 132) = 232 — 132 — 95 = 100 — 95 = 5
е) (629 + 56) – 629 = (629 — 629) + 56 = 56
8. Реши уравнения с комментированием и сделай проверку:
а) (a • 80) : 4 = 120
a • 80 = 120 * 4
a = 480 : 80
а = 6
Проверка:
(6 • 80) : 4 = 120
120 = 120
б) 9 • (560 : b – 5) = 27
560 : b – 5 = 27 : 9
560 : b = 3 + 5
b = 560 : 8
b = 70
Проверка:
9 • (560 : 70 – 5) = 27
27 = 27
в) (14 – c) • 4 – 9 = 19
(14 – c) • 4 = 28
14 – c = 28 : 4
с = 14 — 7
с = 7
Проверка:
(14 – 7) • 4 – 9 = 19
19 = 19
9. Составь программу действий и вычисли:
1 2 5 3 4
а) (6 543 508 + 34 592) : 9 – 700 900 • 70 : 100 = 240270
1) 6543508 + 34592 = 6578100
2) 6578100 : 9 = 730900
3) 700900 * 70 = 49063000
4) 49063000 : 100 = 490630
5) 730900 — 490630 = 240270
4 1 2 3 5
б) 81 650 204 – (54 867 + 295 • 60) : 9 + 2 989 685 = 84631826
1) 295 * 60=17700
2) 54867 + 17700=72567
3) 72567 : 9=8063
4) 81650204 — 8063=81642141
5) 81642141 + 2989685=84631826
10. 1 января 2018 года было понедельником. Каким днём недели будет 1 января 2019 года, 1 января 2020 года, 1 января 2021 года?
1 января 2019 года — это вторник, 1 января 2020 года — среда, 1 января 2021 года — пятница. Дни идут по порядку, кроме 1 января 2021? Потому, что 2020 является високосным годом — в нём 366 дней (добавляется 29 февраля).
Страница 13
1. а) Определи по рисунку, из какого города вышел поезд. Куда и с какой скоростью он идёт? Построй числовой луч и покажи на нём движение поезда.
Едет из Москвы в Вологду, со скоростью 80 км/ч. Строим луч как в учебнике.
б) Пусть s – путь, который прошёл поезд, d – его расстояние до Вологды, D – расстояние до Калуги. Заполни таблицу. Запиши формулы зависимостей каждой из величин s, d, D от времени движения t.
| Время, t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | t |
| Расстояние , s | 0 | 80 | 160 | 240 | 320 | 400 | 480 | s = 80 * t |
| d, км | 480 | 400 | 320 | 240 | 160 | 80 | 0 | d = 480 — 80 * t |
| D, км | 160 | 240 | 320 | 400 | 480 | 560 | 640 | D = 160 + 80 * t |
2. а) Определи по рисунку, из какого города выехал автобус. Куда и с какой скоростью он едет? Построй числовой луч и покажи на нём движение автобуса.
Едет из Москвы в Брянск, со скоростью 60 км/ч.
б) Пусть s – путь, который прошёл автобус, d – его расстояние до Брянска, D – расстояние до Воронежа. Заполни таблицу. Запиши формулы зависимостей каждой из величин s, d, D от времени движения t.
| Время, t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | t |
| Расстояние , s | 0 | 60 | 120 | 180 | 240 | 300 | 360 | s = 60 * t |
| d, км | 360 | 300 | 240 | 180 | 120 | 60 | 0 | d = 360 — 60 * t |
| D, км | 120 | 180 | 240 | 300 | 360 | 420 | 480 | D = 120 + 60 * t |
3. Выполни действия. Проверь результаты с помощью калькулятора.
+181048
49237
230285
в) 700 • 209 530 = 146 671 000
х209530
700
146671000
б) 6 080 010 – 5 550 481 = 529 529
— 6080010
5550481
529529
г) 60 002 400 : 80 = 6000240 : 8 = 750 030
Страница 14
4. Расстояние от посёлка Солнечное до Тучково 18 км, а от Тучково до Маросейкино – в 4 раза больше. Автобус едет из Солнечного в Маросейкино через Тучково со скоростью 45 км/ч. За какое время он проедет весь этот путь?
1) 4 * 18 = 72 (км) — от Тучково до Маросейкино
2) 18 + 72 = 90 (км) — от посёлка Солнечное до Маросейкино
3) 90 : 45 = 2 (ч) — он проедет весь путь
Ответ: 2 часа.
5. Стояка геологов находится на расстоянии 250 км от города. Чтобы добраться до стоянки, геологи сначала ехали из города 3 ч на машине со скоростью 72 км/ч, за тем 2 ч ехали на лошадях со скоростью 9 км/ч, а потом 4 ч шли пешком. С какой скоростью они шли пешком?
1) 3 * 72 = 216 (км) — проехали на машине.
2) 2 * 9 = 18 (км) — проехали на лошадях.
3) 216 + 18 = 16 (км) — шли пешком.
4) 16 : 4 = 4 (ч) — шли пешком.
Ответ: 4 часа.
6. Реши уравнения с комментированием:
а) 540 : (17 – x) = 60
17 – x = 540 : 60
17 – x = 9
х = 17 — 9
х = 8
б) (8 • y – 30) : 9 = 50
8 • y – 30 = 50 * 9
8 • y = 450 + 30
y = 480 : 8
у = 6
7. Выполни действия. Расположи ответы примеров в порядке возрастания и расшифруй имя героя книги. Кто это?
Л = 48756 + 192317 + 392 = 241073 + 392 = 241465
О = 9032016 − 8790560 = 241456
− 9032016
8790560
241456
А = 2705 * 800 = 2164000
х 2705
800
2164000
К = 50860 * 40 = 2034400
х 50850
40
2034400
В = 674814 : 7 = 96402
Ь = 7283700 : 9 = 809300
— 7283700 | 9
72 |809300
— 83
81
— 27
27
0
96402(В) > 241456(О) > 241465(Л) > 809300(Ь) > 2034400(К) > 2164000(А)
Ответ: ВОЛЬКА
* — Костыльков − герой повести-сказка «Старик Хоттабыч»
8. Запиши множество делителей и множество кратных числа 14.
9. A – множество остатков, которые могут получиться при делении на 5, а B – множество остатков, возможных при делении на 7.
а) Задай множества A и B перечислением и запиши элементы с помощью фигурных скобок.
б) Построй диаграмму Эйлера – Венна множеств A и B. Какое из множеств является подмножеством другого?
А является подмножеством В — A ⊂ B
в) Найди A ∩ B и A U B.
а) Расположи 6 элементов в двух множествах так, чтобы в каждом из них было по 5 элементов.
б) Приведи 4 своих варианта расположения 6 элементов в двух множествах.
Страница 15
1. Пчела Майя стала соединять формулы с их названиями. Все линии перепутались. Определи, правильно ли пчела Майя выполнила задание.
Какие ещё формулы ты знаешь?
a = b * q + r, r < b − формула деления с остатком;
P = a * 2 + b * 2 − формула периметра прямоугольника;
S = a * b − формула площади прямоугольника;
P = (a + b) * 2 − формула периметра прямоугольника;
V = a * b * c − формула объема прямоугольного параллелепипеда;
s = v * t − формула пути.
Ответ: Майя правильно выполнила задание.
2. Прочитай задачу и объясни, как составлена таблица:
«Заяц сначала бежал 2 ч со скоростью 24 км/ч, затем 3 ч ехал на велосипеде, а после этого 5 ч ехал на поезде со скоростью 48 км/ч. Всего заяц пробежал и проехал 357 км. С какой скоростью он ехал на велосипеде?»
Используя таблицу, ответь на вопросы:
а) Какой путь пробежал заяц за первые 2 ч?
б) Какой путь он проехал на поезде за последние 5 ч?
в) Какой путь проехал заяц на велосипеде за 3 ч?
г) С какой скоростью он ехал на велосипеде? Составь план решения задачи и запиши решение в тетради. Сделай вывод: как можно решить задачу с помощью таблицы?
План
1) Надо узнать какой путь он проехал на велосипеде, для этого из всего пути вычтем путь который он бежал и ехал на поезде.
2) Поделим путь на время (3 ч)
3) Узнаем скорость передвижения на велосипеде
1) 2 * 24 = 48 (км) — путь который пробежал.
2) 5 * 48 = 240 (км) — путь который проехал на поезде.
3) 357 — (240 + 48) = 69 (км) — путь, который проехал на велосипеде
4) 69 : 3 = 23 (км/ч) — скорость зайца на велосипеде.
Ответ: 23 км/ч.
3. Составь в тетради таблицы и реши задачи:
а) Вертолёт пролетает 840 км за 3 ч, а автомобиль проходит это же расстояние за 7 ч. Чья скорость больше и на сколько?
| s | v | t | |
| Вертолет | 840 | на ? км/ч | 3 |
| Автомобиль | 840 | 7 |
1) 840 : 3 = 280 (км/ч) — скорость вертолета.
2) 840 : 7 = 120 (км/ч) — скорость автомобиля.
3) 280 — 120 = 160 (км/ч) — на столько больше скорость вертолета, чем автомобиля.
Ответ: на 160 км/ч скорость вертолета больше, чем автомобиля.
б) Поезд проходит 320 км за 5 ч. Какое расстояние он пройдёт за 8 ч, двигаясь с этой же скоростью?
| s | v | t | |
| I | 320 | одинаковая | 5 |
| II | 512 | 8 |
1) 320 : 5 = 64 (км/ч) — скорость поезда.
2) 64 * 8 = 512 (км) — проедет поезд за 8 часов.
Ответ: 512 км.
в) Караван верблюдов шёл в первый день 8 ч со скоростью 9 км/ч, во второй день – 6 ч со скоростью 8 км/ч, а в третий день – 9 ч со скоростью 7 км/ч. Какое расстояние прошёл караван за 3 дня?
| s | v | t | |
| I | 72 | 9 | 8 |
| II | 48 | 8 | 6 |
| III | 63 | 7 | 9 |
1) 9 * 8 = 72 (км) — прошел караван в 1 день
2) 6 * 8 = 48 (км) — прошел караван во 2 день
3) 9 * 7 = 63 (км) — прошел караван в 3 день.
4) 72 + 48 + 63 = 183 (км) — прошел караван за 3 дня.
Ответ: 183 км.
4. Реши уравнения с комментированием и сделай проверку:
а) x • 7 – 80 = 340
x • 7 = 340 + 80
x = 420 : 7
х = 6
Проверка:
x • 6 – 80 = 340
340 = 340
б) (900 – y) : 9 = 80
900 – y = 80 * 9
у = 900 — 720
у = 180
Проверка:
(900 – 180) : 9 = 80
80 = 80
в) (350 : y + 10) • 7 = 560
350 : y + 10 = 560 : 7
350 : y = 80 — 10
у = 350 : 70
у = 5
Проверка:
(350 : 5 + 10) • 7 = 560
560 = 560
5. Прочитай числа и расположи их в порядке возрастания: 94 517, 3896, 3 002 650, 302 650, 32 650 Найди разность наибольшего и наименьшего из этих чисел.
94517 − девяносто четыре тысячи пятьсот семнадцать,
3896 − три тысячи восемьсот девяносто шесть,
3002650 − три миллиона две тысячи шестьсот пятьдесят,
32650 − тридцать две тысячи шестьсот пятьдесят.
3896 < 3650 < 94517 < 3002650
3002650 − 3896 = 2998754
Страница 17
6. 1) Запиши число 40 560 в виде суммы разрядных слагаемых.
2) Сколько единиц в разряде сотен числа 40 560?
5 единиц в разряде сотен числа 40560.
Сколько всего сотен в этом числе?
Всего 405 сотен в чисел 40560
а) в сотнях и единицах;
б) в тысячах и единицах.
3) Вырази величины в указанных единицах измерения:
а)
40560 м = 40 км 560 м;
40560 мм = 40 м 560 мм;
40560 мм = 405 дм 60 мм.
б)
40560 кг = 40 т 560 кг;
40560 кг = 405 ц 60 кг;
40560 г = 40 кг 560 г.
7. Найди пропущенные цифры при делении с остатком углом. Сделай проверку по формуле деления с остатком: a = b • c + r, r < b.
711842 : 9 = 79093 (ост.5)
Проверка: 79093 * 9 + 5 = 711837 + 5 = 711842
40715 : 8 = 5089 (ост.3)
Проверка: 5089 * 8 + 3 = 40712 + 3 = 40715
8. Запиши множество делителей и множество кратных числа 15.
9. Расшифруй имя славного защитника Руси. Что ты о нём знаешь?
У = 247 + 53 = 300
+247
53
300
О = 400 − 265 = 135
−400
265
135
Ь = 218 + 26 = 244
+218
26
244
Л = 325 − 43 = 282
−325
43
282
Я = 350 : 7 * 8 = 50 * 8 = 400;
Ц = 9 * 4 + 82 = 36 + 82 = 118;
К = 172 − 72 : 4 = 172 − 18 = 154
Е = 567 − 60 * 4 = 567 − 240 = 327
−567
240
327
И = (320 : 40) * 8 = 8 * 8 = 64;
Т = 900 : (25 * 6) = 900 : 150 = 6;
М = 90 * 2 : 30 * 70 = 180 : 30 * 70 = 6 * 70 = 420.
Ответ: ИЛЬЯ МУРОМЕЦ − один из главных героев былинного эпоса, русский богатырь.
10. В каком квартале года наибольшее число дней, а в каком – наименьшее? Рассмотри случаи високосного и невисокосного года
I квартал:
Январь − 31 день;
Февраль − 28 дней (в високосном году 29 дней);
Март − 31 день.
31 + 28 + 31 = 59 + 31 = 90 (дней) − в первом квартале в обычном году;
31 + 29 + 31 = 60 + 31 = 91 (день) − в первом квартале в високосном году.
II квартал:
Апрель − 30 дней;
Май − 31 день;
Июнь − 30 дней.
30 + 31 + 30 = 61 + 30 = 91 (день) − во втором квартале.
III квартал:
Июль − 31 день;
Август − 31 день;
Сентябрь − 30 дней.
31 + 31 + 30 = 62 + 30 = 92 (дня) − в третьем квартале.
IV квартал:
Октябрь − 31 день;
Ноябрь − 30 дней;
Декабрь − 31 день.
31 + 30 + 31 = 61 + 31 = 92 (дня) − в четвертом квартале.
Обычный год:
больше всего дней в III и IV кварталах (по 92 дня);
меньше всего дней в I квартале (90 дней).
Високосный год:
больше всего дней в III и IV кварталах (по 92 дня);
меньше всего дней в I и II кварталах (по 91 дню).
Страница 18
1. а) Ира прошла 320 м за 5 мин, а Петя – 225 м за 3 мин. У кого из ребят скорость больше и на сколько?
1) 320 : 5 = 64 (м/мин) — скорость Иры.
2) 225 : 3 = 75 (м/мин) — скорость Пети.
3) 75 — 64 = 11 (м/мин) — скорость Пети больше, чем Иры.
Ответ: на 11 м/мин.
б) Орёл за 9 с пролетел 270 м, а сокол за это же время пролетел 189 м. На сколько метров в секунду скорость сокола меньше скорости орла?
1) 270 : 9 = 30 (м/с) − скорость орла;
2) 189 : 9 = 21 (м/с) − скорость сокола;
3) 30 − 21 = 9 (м/с) − скорость сокола меньше скорости орла.
Ответ: на 9 м/с
в) Первый лыжник за 3 ч пробежал 51 км, а второй лыжник за это же время пробежал на 6 км больше. На сколько километров в час скорость второго лыжника больше скорости первого?
1) 51 : 3 = 17 (км/ч) — скорость первого лыжника;
2) 51 + 6 = 57 (км) — пробежал второй лыжник;
3) 57 : 3 = 19 (км/ч) — скорость второго лыжника;
4) 19 − 17 = 2 (км/ч) — скорость второго лыжника больше, чем первого.
Ответ: на 2 км/ч.
2. а) От деревни до станции 4 км. Ваня идёт из деревни на станцию со скоростью 80 м/мин. Какое расстояние ему останется пройти через полчаса после выхода? Сколько времени ему потребуется, чтобы пройти оставшееся расстояние?
Зная что: пол часа = 30 мин и 4 км = 4000 м
1) 30 * 80 = 2400 (м) — пройдет Ваня за полчаса.
2) 4000 − 2400 = 1600 (м) — останется пройти Ване.
3) 1600 : 80 = 20 (мин) − время, через которое Ваня пройдет оставшееся расстояние.
Ответ: 1600 м; за 20 мин.
б) Автомобиль за 6 ч проехал 480 км. Какое расстояние мог бы проехать автомобиль за это же время, если бы увеличил скорость на 12 км/ч?
1) 480 : 6 = 80 (км/ч) — скорость автомобиля;
2) 80 + 12 = 92 (км/ч) — увеличенная скорость автомобиля;
3) 92 * 6 = 552 (км) — мог бы проехать автомобиль, если бы ехал с увеличенной скоростью.
Ответ: 552 км.
а) Таня шла сначала по шоссе a км, а потом по просёлку b км. С какой скоростью шла Таня, если весь путь занял t часов?
б) Костя шёл лесом a км, а полем на b км больше. Весь путь занял t часов. С какой скоростью шёл Костя?
в) Расстояние от села Горшково до деревни Светлая a км, а от деревни Светлая до города в b раз меньше. Грузовик проехал от Горшково до города через деревню Светлая со скоростью v км/ч. Сколько времени ехал грузовик?
Страница 19
4. Составь выражение и найди его значение при данных значениях букв:
а) Лодка проплывает a км вниз по реке со скоростью b км/ч, а возвращается со скоростью c км/ч. Какое время затратит лодка на весь путь туда и обратно? (a = 30, b = 10, c = 6)
(a : b) + (а : с) = (30 : 10) + (30 : 6) = 3 + 5 = 8 (ч)
Ответ: 8 часов.
б) Валя прошла за k часов x км, а Серёжа за то же время прошёл y км. На сколько скорость Серёжи больше скорости Вали? (x = 12, y = 15, k = 3)
(y : k) — (x : k) = (15 : 3) — (12 : 3) = 5 — 4 = 1 (км/ч)
Ответ: на 1 км/ч.
в) Машина проехала за n часов d км. Какое расстояние она проедет за m часов, если будет ехать с той же скоростью? (d = 240, n = 4, m = 7)
d : n * m = 240 : 4 * 7 = 60 * 7 = 420 (км)
Ответ: 420 км.
5. Пусть a – длина прямоугольника, а b – его ширина. Объясни смысл выражений:
a + b — длина и ширина прямоугольника
a • 2 + b • 2 — периметр
a • b — площадь
a – b — на сколько длина больше ширины
(a + b) • 2 — периметр
a : b — во сколько раз длина больше ширины
6. Найди площадь закрашенных фигур:
6 * 12 — 4 * 4 = 72 — 16 = 56 (м 2 ) — площадь фигуры.
Ответ: 56 м 2 .
80 * 96 — 40 * 28 = 7680 — 1120 = 6560 (см 2 ) — площадь фигуры.
Ответ: 6560 см 2 .
7. Реши уравнения с комментированием и проверкой:
а) (150 : x + 6) : 7 = 8
150 : x + 6 = 8 * 7
150 : x = 56 — 6
х = 150 : 50
х = 3
Проверка:
(150 : 3 + 6) : 7 = 8
8 = 8
б) 800 – (y • 8 – 20) = 100
y • 8 – 20 = 800 — 100
y • 8 = 720
y = 720 : 8
y = 90
Проверка:
800 – (90 • 8 – 20) = 100
100 = 100
8. Составь программу действий и вычисли:
4 7 1 2 5 8 6 3
а) 0 • 19 + (45 : 1 – 0) • 1 – 18 • (12 : 12) = 27
1) 45 : 1 = 45
2) 45 — 0 = 45
3) 12 : 12 = 1
4) 0 * 19 = 0
5) 45 * 1 = 45
6) 18 * 1 = 18
7) 0 + 45 = 45
8) 45 — 18 = 27
5 8 1 3 2 6 9 7 4
б) 1 • 0 + (3 • 8 – 6 • 4) • 5 – 0 : (945 – 732) = 0
1) 3 * 8 = 24
2) 6 * 4 = 24
3) 24 — 24 = 0
4) 945 — 732 = 213
5) 1 * 0 = 0
6) 0 * 5 = 0
7) 0 : 213 = 0
8) 0 + 0 = 0
9) 0 — 0 = 0
9. Запиши множество делителей и множество кратных числа 16.
10. Установи закономерность, по которой расставлены числа в таблице. Найди пропущенное число.
| 3 | 5 | 7 | 9 |
| 9 | 25 | 49 | 81 |
| 4 | 6 | 8 | 10 |
| 15 | 35 | 63 | 99 |
| 2 | 3 | 4 | 5 |
| 5 | 10 | 17 | 26 |
Страница 20
1. а) После вспышки молнии Марина услышала гром через 5 с. На каком расстоянии от неё ударила молния? (Скорость распространения звука в воздухе равна 330 м/с.)
5 * 330 = 1650 (м) − расстояние от Марины до молнии.
1650 м = 1 км 650 м
Ответ: 1 км 650 м.
б) Скорость распространения света 300 000 км/с. На Солнце произошла вспышка. Через какое время её увидят на Земле, если расстояние от Земли до Солнца равно 150 000 000 км?
150 000 000 : 3 00000 = 500 (с) — увидят вспышку на Земле.
Ответ: через 500 секунд или 8 мин 20 секунд
2. а) Грузовик проехал расстояние из города A в город B со скоростью 45 км/ч за 4 часа. Обратно из B в A он возвращался по той же дороге со скоростью на 15 км/ч больше. На сколько меньше времени затратил грузовик на обратный путь?
1) 4 * 45 = 180 (км) — весь путь грузовика.
2) 45 + 15 = 60 (км) — скорость на обратном пути
3) 180 : 60 = 3 (ч) — времени ушло на обратный путь
4) 4 — 3 = 1 (ч) — на столько меньше грузовик затратил времени на обратный путь
Ответ: на 1 час.
б) Автобус проехал 432 км за 8 часов. На сколько километров в час он должен был увеличить скорость, чтобы проехать это расстояние на 2 часа быстрее?
1) 432 : 8 = 54 (км/ч) — с такой скоростью ехал автобус 432 километра.
2) 8 * 2 = 6 (ч) — он должен проехать 432 километра, чтобы проехать это расстояние на 2 часа быстрее.
3) 432 : 6 = 72 (км/ч) — должна быть скорость.
4) 72 — 54 = 18 (км/ч) — на столько должен увеличить скорость автобус
Ответ: на 18 километров в час.
3. Вычисли устно:
S = 5 * 5 = 25 м 2
P = (5 + 5) * 2 = 20 м
P = 28 (тогда сторона квадрата 28 : 2 : 2 = 7 см)
S = 7 * 7 = 49 см 2
S = 12 дм 2 (тогда вторая сторона 12 : 6 = 2 дм)
P = (2 + 6) * 2 = 16 (дм)
P = 18 см (тогда вторая сторона (18 — 4*2) : 2 = 5 см)
S = 5 * 4 = 20 см 2
4. Автомобиль должен за 7 часов проехать 630 км. Первые 2 ч он ехал со скоростью 70 км/ч, а в следующие 3 ч увеличил скорость на 20 км/ч. С какой скоростью автомобиль должен ехать оставшийся путь, чтобы прибыть в пункт назначения вовремя?
1) 2 * 70 = 140 (км) − проехал автомобиль в первые 2 часа;
2) 70 + 20 = 90 (км/ч) − скорость автомобиля во вторые 3 часа;
3) 3 * 90 = 270 (км) − проехал автомобиль во вторые 3 часа;
4) 630 − (140 + 270) = 630 − 410 = 220 (км) − осталось проехать автомобилю;
5) 7 − (2 + 3) = 7 − 5 = 2 (ч) − осталось проехать автомобилю;
6) 220 : 2 = 110 (км/ч) − скорость, с которой должен ехать автомобиль оставшийся путь.
Ответ: 110 км/ч.
Страница 21
5. Иван Иванович отправился из дома на озеро Медвежье ловить рыбу. Три часа он ехал на поезде со скоростью 75 км/ч, а потом 2 часа шёл по лесу со скоростью 4 км/ч. Какой путь проделал Иван Иванович от дома до озера?
1) 75 * 3 = 225 (км) — ехал на поезде.
2) 4 * 2 = 8 (км) — шел пешком.
3) 225 + 8 = 233 (км) — путь проделал Иван Иванович от дома до озера.
Ответ: 233 км.
6. Составь выражение и найди его значение, если a = 90: «Велосипедист проехал расстояние, равное a км, за 5 ч, а автобус – за 2 ч. На сколько километров в час скорость автобуса больше скорости велосипедиста?»
90 : 2 — 90 : 5 = 45 — 18 = 27 (км/ч) — скорость автобуса больше скорости велосипедиста.
Ответ: на 27 км/ч.
7. Прочитай выражения и найди их значения:
а) 800 • n, если n = 70 540
б) 278 100 : c, если c = 90
8. Реши уравнения с комментированием и сделай проверку:
а)
(200 + 20 • a) : 6 = 60
200 + 20 • a = 60 * 6
20 • a = 360 — 200
a = 160 : 20
а = 8
Проверка:
(200 + 20 • 8) : 6 = 60
60 = 60
б)
320 : (b • 8 – 40) = 10
b • 8 – 40 = 320 : 10
b • 8 = 32 + 40
b = 72 : 8
b = 9
Проверка:
320 : (9 • 8 – 40) = 10
10 = 10
9. а) Туристы вышли из посёлка Дачное. В каком направлении и с какой скоростью они идут? Построй числовой луч и покажи на нём движение туристов.
Идут с Дачного в Грибцово, со скоростью 6 км/ч.
б) Пусть s км – путь, пройденный туристами, d км – расстояние от туристов до Грибцова, а D км – до Земляничной Поляны. Заполни таблицу. Запиши формулу зависимости каждой из величин s, d, D от времени движения t.
| t ч | 0 | 1 | 2 | 3 | 4 | 5 | t |
| s км | 0 | 6 | 12 | 18 | 24 | 30 | 6 * t |
| d км | 30 | 24 | 18 | 12 | 6 | 0 | 30 — 6 * t |
| D км | 30 | 36 | 42 | 48 | 54 | 60 | 30 + 6 * t |
10. Запиши множество делителей и множество кратных числа 17.
11. Назови число, предшествующее самому маленькому 15-значному числу.
100 000 000 000 000 — самое маленькое 15-значное.
99 999 999 999 999 — предшествует самому маленькому 15-значному. (девяносто девять триллионов девятьсот девяносто девять миллионов девятьсот девяносто девять тысяч девятьсот девяносто девять)
Страница 22
1. Повтори таблицу мер длины, массы и времени. Вырази данные значения величин в указанных единицах измерения:
а)
8 км 16 м = 8016 м
5 м 9 мм = 5009 мм
2 т 3 ц 6 кг = 2306 кг
4 ц 7 кг 8 г = 407 008 г
б)
2 сут. 9 ч 25 мин = 2 * 24 * 60 + 9 * 60 + 25 = 2880 + 540 + 25 = 3 445 мин
3 ч 12 мин 46 с = 3 * 60 * 60 + 46 = 10 800 + 46 = 10 846 с
870 мин = 14 ч 30 мин
3520 с = 58 мин 40 с
2. а) Лыжник прошёл 18 км за 2 часа. Какое расстояние он пройдёт за такое же время, если увеличит скорость на 3 км/ч?
1) 18 : 2 = 9 (км/ч) — скорость лыжника.
2) 9 + 3 = 12 (км/ч) — будет скорость лыжника, если он ее увеличит на 3 км/ч
3) 12 * 2 = 24 (км) — пройдет лыжник.
Ответ: 24 км.
б) Моторная лодка прошла по течению реки 5 ч со скоростью 24 км/ч. На обратный путь она затратила на 1 час больше времени. Чему равна скорость моторной лодки против течения реки?
1) 5 * 24 = 120 (км) — прошла по течению реки.
2) 120 : 6 = 20 (км/ч) — была скорость на обратном пути, против течения.
Ответ: 20 км/ч.
3. Вычисли устно:
Слева: 9 * 3 * 2 = 54 (м 3 ) — объем параллелепипеда.
Справа: 12 * 5 — 6 * 2 = 60 — 12 = 48 (дм 2 ) — площадь закрашенная зеленым цветом.
4. Катер прошёл путь между двумя пристанями со скоростью 30 км/ч, а обратный путь – со скоростью на 10 км/ч большей. Расстояние между этими пристанями равно 240 км. Какое время затратил катер на путь туда и обратно?
1) 240 : 30 = 8 (ч) — катер шел в одном направлении.
2) 30 + 10 = 40 (км/ч) — скорость катера в обратном направлении.
3) 240 : 40 = 6 (ч) — катер шел в обратном направлении.
4) 8 + 6 = 14 (ч) — катер шел туда и обратно.
Ответ: 14 часов.
5. Прочитай выражения и найди их значения:
а) 10 000 – x : 70, если x = 644 560
При x = 644 560
10 000 – x : 70 = 10 000 – 644 560 : 70 = 10 000 — 9 208 = 792
б) (y • 6004) : 500, если y = 4000
При y = 4000
(y • 6004) : 500 = (4000 • 6004) : 500 = 24 016 000 : 500 = 48 032
6. Реши уравнения с комментированием и сделай проверку:
а) (n : 4 – 35) • 6 = 150
1. Вначале переместим из левой части в правую число 6, поделив на него 150, получим:
(n : 4 — 35) * 6 = 150,
n : 4 — 35 = 150 / 6,
n : 4 — 35 = 25.
2. Теперь переместим в правую часть вычитаемое значение 35, прибавив его к 25, получим:
n : 4 = 35 + 25,
n : 4 = 60.
Остается только умножить делитель левой части на 60, чтобы выяснить, чему равен n:
n = 4 * 60,
n = 240.
Проверка:
(240 : 4 — 35) * 6 = 150,
(60 — 35) * 6 = 150,
25 * 6 = 150,
150 = 150, правильно, значит решение верное.
Ответ: в результате получили значение n, равное 240.
б) 90 • (m – 8) + 60 = 510
Чтобы решить 90 * (m — 8) + 60 = 510 уравнение используем тождественные преобразования.
Первым действием переносим 60 в правую часть уравнения и меняем его знак на противоположный.
90 * (m — 8) = 510 — 60;
90 * (m — 8) = 450;
m — 8 = 450 : 90;
m — 8 = 5;
И последним действием перенесем 8 в правую часть уравнения и сменим для этой цифры знак на «+».
m = 5 + 8;
m = 13.
Проверка:
90 * (13 — 8) = 510 — 60
450 = 450 правильно, значит решение верное.
Ответ: в результате получили значение m, равное 13.
Страница 23
7. Составь и реши уравнения:
а) Миша задумал число, умножил его на 5 и полученное произведение вычел из 41. В результате у него получилось 16. Какое число за думал Миша?
Обозначим задуманное число через х. После того, как Миша умножил задуманное число на 5, в результате получилось 5* х. После того, как Миша полученное произведение вычел из 41, в результате получилось 41 — 5х. Также в условии задачи сказано, что в результате всех этих действий у Миши получилось 16, следовательно, можем составить следующее уравнение:
Решаем полученное уравнение:
5 * х = 41 — 16;
5 * х = 25.
х = 25 : 5;
х = 5.
Ответ: Миша задумал число 5.
б) Галя за думала число, вычла его из 50, результат разделила на 7. У неё получи лось 7. Какое число задумала Галя?
Задуманное число примем за Х, составим и решим уравнение:
(50 — Х) : 7 = 7
(50 — Х) = 7 * 7
50 — Х = 49
Х = 1
Проверим решение уравнения:
(50 -1) : 7 = 7
7 = 7.
Ответ: Галя задумала число 7
в) Тимоша задумал число, затем разделил 54 на задуманное число, при ба вил к результату 26 и полученную сумму раз де лил на 8. В ответе у него получилось 4. Какое число задумал Тимоша?
(54 : Х + 26) : 8 = 4
54 : Х + 26 = 4 * 8
54 : Х +26 = 32
54 : Х = 32 — 26
54 : Х = 6
Х = 9.
Проверим решение уравнения:
(54 : 9 + 26) : 8 = 4
4 = 4.
Ответ: Тимоша задумал 4.
8. Составь программу действий и вычисли:
1 2 3 7 9 4 6 5 8
а) (1800 : 2 : 30 + 18) : 6 + (70 • 7 – 140 : 2) : 60 = 15
1) 1800 : 2 = 900
2) 900 : 30 = 30
3) 30 + 18 = 48
4) 48 : 6=8
5) 70 * 7 = 490
6) 140 : 2 = 70
7) 490 — 70 = 420
8) 420 : 60 = 7
9) 8 + 7 = 15
2 1 6 7 9 3 5 4 8
б) (60 – 16 : 4) : 8 • 40 – (80 • 8 – 20 • 5) : 6 = 190
1) 16 : 4 = 4
2) 60 — 4 = 56
3) 80 * 8 = 640
4) 20 * 5 = 100
5) 640 — 100 = 540
6) 56 : 8 = 7
7) 40 * 7 = 280
8) 540 : 6 = 90
9) 280 — 90 = 190
а) Стрекоза пролетает a км за 2 ч. Какое расстояние она пролетит за 5 ч, если будет лететь с той же скоростью?
б) Заяц пробежал b км за 3 ч, а волк пробежал то же расстояние за 4 ч. У кого из них скорость больше и на сколько?
в) Крокодил Гена проехал 3 ч на поезде со скоростью n км/ч и 2 ч на автобусе со скоростью m км/ч. Сколько всего километров он проехал?
г) Черепаха Тортила 5 ч ползла со скоростью c км/ч. Всего ей надо проползти d км. Какое расстояние ей ещё осталось проползти?
10. Запиши множество делителей и множество кратных числа 18.
11. Найди пропущенные цифры. Проверь с помощью калькулятора.
12. Пять товарищей спускались с горы на санках. Игорь проехал дальше Романа, но ближе, чем Олег. Костя проехал меньше, чем Роман, а Илья – дальше Олега. Кто из них проехал дальше всех, а кто – ближе всех?
Если Игорь проехал дальше Романа, но меньше, чем Олег, то дети располагаются следующим образом:
Роман, Игорь, Олег.
Если Илья проехал дальше, чем Олег, то поставим его имя после имени Олег:
Роман, Игорь, Олег, Илья.
Костя проехал меньше, чем Роман, значит его имя поставим в начало:
Костя, Роман, Игорь, Олег, Илья.
ОТВЕТ: дальше всех проехал Илья, меньше всех проехал Костя.
Страница 24
1. а) Вертолёт пролетел 840 км за 4 часа, а автобус проехал расстояние в 2 раза меньшее, затратив на 2 часа больше. Во сколько раз скорость автобуса меньше скорости вертолёта?
1) 840 : 4 = 210 (км/ч) — скорость вертолета.
2) 840 : 2 = 420 (км) — проехал автобус.
3) 4 + 2 = 6 (ч) — ехал автобус.
4) 420 : 6 = 70 (км/ч) — скорость автобуса.
5) 210 : 70 = в 3 (раза) — скорость автобуса меньше скорости вертолета
Ответ: в 3 раза.
б) Лыжник пробежал 36 км за 2 ч, а пешеход прошёл половину этого расстояния за время в 3 раза большее. На сколько километров в час скорость пешехода меньше скорости лыжника?
1) 36 : 2 = 18 (км/ч) — скорость лыжника
2) 36 : 2 = 18 (км) — половина пути.
3) 2 * 3 = 6 (ч) — шел пешеход
4) 18 : 6 = 3 (км/ч) скорость пешехода.
5) 18 — 3 = 15 (км/ч) — на столько километров в час скорость пешехода меньше скорости лыжника.
Ответ: 1на 15 км/ч.
а) После того как поезд проехал 4 часа со скоростью n км/ч, ему ещё осталось проехать b км. Чему равен весь путь поезда?
б) Спортсмен бежал 2 часа со скоростью v км/ч. Длина всей дистанции равна m км. Сколько километров ему ещё осталось пробежать?
в) Самолёт пролетел s км за 3 часа, а в обратную сторону – за 2 часа. На сколько километров в час больше была его скорость на обратном пути?
3. Выполни действия:
а) 1 ч = 60 мин
5 ч 12 мин = 5 * 60 + 12 = 300 + 12 = 312 мин
3 ч 48 мин — 3 * 60 + 47 = 180 + 47 = 227 мин
5 ч 12 мин — 3 ч 48 мин = 312 мин — 227 мин = 85 мин = 1 ч 25 мин
б) 1 мин = 60 с
16 мин 39 с = 16 * 60 + 39 = 960 + 39 = 999 с
4 мин 56 с = 4 * 60 + 56 = 240 + 56 = 296 с
16 мин 39 с + 4 мин 56 с = 999 с + 296 с = 1295 с = 21 мин 35 с
в) 1 ц = 100 кг; 1 т = 1000 кг; 1 т = 10 ц
42 ц 94 кг = 42 * 100 + 94 = 4200 + 94 = 4294 кг
2 т 6 кг = 2 * 1000 + 6 = 2000 + 6 = 2006 кг
42 ц 94 кг + 2 т 6 кг = 4294 кг + 2006 кг = 6300 кг = 63 ц = 6 т 3 ц
г) 1 т = 1000 кг; 1 ц = 100 кг
12 т 50 кг = 12 * 1000 + 50 = 12 000 + 50 = 12 050 кг
52 ц 90 кг = 52 * 100 + 90 = 5200 + 90 = 5290 кг
12 т 50 кг — 52 ц 90 кг = 12 050 кг — 5290 кг = 6760 кг = 6 т 7 ц 60 кг
4. Составь программу действий и вычисли:
5 1 3 2 8 6 9 4 7
а) 80 : (16 • 4 + 320 : 20) + 74 • 0 – (18 – 18) : 30 = 1
1) 16 * 4 = 64
2) 320 : 20 = 16
3) 64 + 16 = 80
4) 18 — 18 = 0
5) 80 : 80 = 1
6) 74 * 0 = 0
7) 0 : 30 = 0
8) 1 + 0 = 1
9) 1 — 0 = 1
5 8 6 1 9 7 2 4 3
б) 0 : 48 + 50 • (10 000 – 9999) – 40 : (27 • 3 – 320 : 4) = 10
1) 10 000 — 9 999 = 1
2) 27 * 3 = 81
3) 320 : 4 = 80
4) 81 — 80 = 1
5) 0 : 48 = 0
6) 50 * 1 = 50
7) 40 : 1 = 40
8) 0 + 50 = 50
9) 50 — 40 = 10
5. Реши уравнения с комментированием и сделай проверку:
Вначале перенесем делитель 3 в правую часть, умножив его на 80, получим значение выражения в скобках:
(90 * b + 60) : 3 = 80,
90 * b + 60 = 3 * 80,
90 * b + 60 = 240.
Теперь перенесем слагаемое 60 в правую сторону, получим:
90 * b = 240 — 60,
90 * b = 180.
Поделим значение произведения на множитель 90, получим значение b:
b = 180 : 90,
b = 2.
Проверка:
(90 * 2 + 60) : 3 = 80,
(180 + 60) : 3 = 80,
240 : 3 = 80,
80 = 80, верно.
Ответ: b = 2.
б) 1400 : (35 – y) – 29 = 41
Перенесем 29 в правую часть уравнения и сменим его знак на плюс.
1400 : (35 — y) = 41 + 29
1400 : (35 — y) = 70
Разность (35 — y) рассмотрим как неизвестный делитель:
35 — y = 1400 : 70
35 — y = 20
Перенесем у в правую часть уравнения и изменим его знак на минус. Для удобства восприятия поменяем стороны уравнения разделенные » tabs article3803-tabs23″>
Страница 25
7. Длина коробки, имеющей форму прямоугольного параллелепипеда, равна 30 см, а ширина – 20 см.
1) Чему равна высота коробки, если её объём равен 7200 см3?
1) 30 * 20 = 600 (см 2 ) — площадь грани.
2) 7200 : 600 = 12 (см) — высота коробки.
Ответ: 12 см.
2) Какую площадь и какой периметр имеет дно коробки?
1) 30 * 20 = 600 (см 2 ) — площадь грани (дна).
2) (30 + 20) * 2 = 100 (см) — периметр дна.
Ответ: 600 см и 100 см
3) Коробку надо перевязать лентой, как показано на рисунке. Какой длины должна быть эта лента, если на узел и бант надо дополнительно предусмотреть 26 см?
12 * 4 + 30 * 2 + 20 * 2 + 2 6 = 48 + 60 + 40 + 26 = 148 + 26 = 174 (см) — длиной должна быть эта лента.
Ответ: 174 см
8. Сравни выражения, не выполняя вычислений. Обоснуй свой ответ.
3974 + 815 = 815 + 3794 — числа в суммах одинаковые
76 012 – 32 < 76 012 – 23 — когда вычитаем из одинакового числа большее, то получается меньшее значение.
9083 – 96 < 9100 – 96 — когда вычитаем из меньшего числа тоже значение, что из большего, то получается меньшее значение.
786 • 29 > 786 + 29 — в 29 раз всегда больше, чем на 29
3420 : 6 < 3420 • 2 — увеличение в 6 раз больше, чем уменьшение в два раза.
2158 : 26 > 2158 : 83 — деление на меньшее значение, всегда дает больший результат.
9. Запиши множество делителей и множество кратных числа 19.
10. Найди площадь прямоугольного участка по указанным размерам. Сколь ко раз личных способов решения имеет эта задача? Что ты замечаешь?
Задача имеет три решения, так как здесь можно выделить 3 прямоугольника.
1 Решение:
6 * 38 = 228 (м 2 ) площадь маленького прямоугольника.
Ответ: 228 м 2 .
2 Решение:
50 * 38 = 1900 (м 2 ) площадь среднего прямоугольника.
Ответ: 1900 м 2 .
3 Решение:
(50 + 6) * 38 = 2128 (м 2 ) площадь большого прямоугольника.
Ответ: 2128 м 2 .
Замечаю, что площадь среднего и малого прямоугольника составляет площадь большого прямоугольника.
11. Найди площадь прямоугольника, разбивая его на части удобным способом:
Удобно разбить на 4 прямоугольника, проведя границу по разрядам величин сторон.
Получаем:
90 * 70 + 70 * 7 + 7 * 5 + 90 * 5 = 6300 + 490 + 35 + 450 = 7 275 (дм 2 ) — площадь прямоугольника.
Ответ: 7 275 дм 2 .
12. Вычисли. Расположи ответы в порядке убывания и расшифруй имя сказочного героя. Из какой он сказки?
Г 3052 * 600 = 1 831 200
У 19 050 * 50 = 952 500
Д 5 632 084 – 5 294 352 = 337 732
В 94 203 + 186 902 + 56 618 = 337 723
И 647 040 : 8 = 80 880
Н 313 920 : 4 = 78 480
ГУДВИН. Сказка: Волшебник изумрудного города.
13. D – множество девочек класса, M – множество мальчиков этого же класса. Что представляют собой множества D M и D M?
D∩M = ∅ (не может быть пересечение девочек и мальчиков);
DUM = множество учеников в классе.
14. В вазе лежало 20 слив. Наташа взяла сначала четверть всех слив, а потом – треть от оставшихся. Сколько всего слив взяла Наташа?
1) 20 : 4 = 5 (с.) — взяла сначала.
2) 20 — 5 = 15 (с.) — осталось.
3) 15 : 3 = 5 (с.) — взяла второй раз.
4) 5 + 5 = 10 (с.) — взяла всего
Ответ: 10 слив.
Страница 26
1. а) Объясни по рисунку, как умножить число на сумму, и выполни умножение:
Для удобства вычисления можно разбить числа в произведении на удобные числа таким образом, чтобы можно было вынести одно целое число, которое удобно будет умножать на разложенные числа. а • (b + c) = a • b + a • c
б) Используя рисунок, объясни способ записи умножения на двузначное число в столбик:
Чтобы умножить любое число на двузначное, можно умножить это число сначала на единицы, а потом на десятки и полученные произведения сложить. В записи суммы число десятков сдвигают на 1 разряд влево
2. В кинотеатре 18 рядов по 32 места в каждом ряду. Сколько всего мест в кинотеатре?
Найди в данной записи ответы на вопросы:
Сколько мест в 8 рядах?
8 * 32 = 256 (м.) — в 8 рядах
Сколько мест в 10 рядах?
10 * 32 = 320 (м.) — в 10 рядах
Сколько всего мест в кинотеатре?
(8 + 10) * 32 = 8 * 32 + 10 * 32 = 256 + 320 = 576 (м.) — всего в кинотеатре.
Ответ: 576 мест.
Страница 27
3. Правильно ли Максим решил и прокомментировал пример?
1. Умножим 145 на 7 единиц, получим 1015 единиц.
2. Умножим 145 на 2 десятка, получим 290 десятков. Записываем число 290 со сдвигом на 1 разряд влево.
3. Складываем полученные числа.
Ответ: 3915.
4. Реши примеры с комментированием:
1. Умножим 92 на 9 единиц, получим 828 единиц.
2. Умножим 92 на 8 десятков, получим 736 десятков. Записываем число 736 со сдвигом на 1 разряд влево.
3. Складываем полученные числа.
Ответ: 8188.
1. Умножим 57 на 5 единиц, получим 285 единиц.
2. Умножим 57 на 9 десятков, получим 513 десятков. Записываем число 513 со сдвигом на 1 разряд влево.
3. Складываем полученные числа.
Ответ: 5415.
в) 138 • 56 = 7 728
1. Умножим 138 на 6 единиц, получим 1242 единиц.
2. Умножим 138 на 5 десятков, получим 690 десятков. Записываем число 690 со сдвигом на 1 разряд влево.
3. Складываем полученные числа.
Ответ: 7728.
г) 296 • 23 = 6808
1. Умножим 296 на 3 единиц, получим 888 единиц.
2. Умножим 296 на 2 десятка, получим 592 десятков. Записываем число 592 со сдвигом на 1 разряд влево.
3. Складываем полученные числа.
Ответ: 6808.
д) 906 • 15 = 13590
1. Умножим 906 на 5 единиц, получим 4530 единиц.
2. Умножим 906 на 1 десяток, получим 906 десятков. Записываем число 906 со сдвигом на 1 разряд влево.
3. Складываем полученные числа.
Ответ: 13590.
е) 709 • 84 = 59 556
1. Умножим 709 на 4 единицы, получим 2836 единиц.
2. Умножим 709 на 8 десятков, получим 5672 десятков. Записываем число 5672 со сдвигом на 1 разряд влево.
3. Складываем полученные числа.
Ответ: 59556
ж) 2384 • 47 = 112 048
1. Умножим 2384 на 7 единиц, получим 16688 единиц.
2. Умножим 2384 на 4 десятка, получим 9536 десятков. Записываем число 9536 со сдвигом на 1 разряд влево.
3. Складываем полученные числа.
Ответ: 13590
з) 9051 • 72 = 651 672
1. Умножим 9051 на 2 единицы, получим 18102 единиц.
2. Умножим 9051 на 7 десятков, получим 63357 десятков. Записываем число 63357 со сдвигом на 1 разряд влево.
3. Складываем полученные числа.
Ответ: 651672
5. а) Лыжники были в походе 7 дней. Каждый день они шли по 6 ч со скоростью 9 км/ч. Сколько километров прошли лыжники?
Составим выражение.
9 * 6 * 7 = 54 * 7 = 378 (км) — прошли лыжники.
Ответ: 378 км
б) Миша пробежал 8 кругов со скоростью 200 м/мин. Сколько времени он бежал, если длина одного круга 400 м?
1) 400 : 200 = 2 (мин) — Миша бежал 1 круг.
2) 2 * 8 = 16 (мин) — бежал Миша.
Ответ: 16 минут.
6. Расстояние от Москвы до Новосибирска 3320 км. Поезд проходит его за 40 ч, а самолёт пролетает – в 10 раз быстрее. На сколько часов меньше лететь до Новосибирска самолётом, чем ехать поездом? Во сколько раз скорость поезда меньше скорости самолёта?
1) 40 : 10 = 4 (ч) — летит самолет
2) 40 — 4 = 36 (ч) — на столько часов меньше летит самолет.
3) 40 : 4 = 10 (р.) — быстрее прилетит самолет, значит его скорость в 10 раз больше.
Ответ: 36 ч , в 10 раз.
7. Составь и реши уравнения:
а) На сколько надо умножить число 60, чтобы получить 4320?
б) Какое число надо разделить на 700, чтобы получить 506?
в) На сколько надо разделить 8500, чтобы получить 500?
8. Запиши множество делителей и множество кратных числа 20.
9. Выполни действия:
а) 4 ч 58 мин + 2 ч 17 мин – 3 ч 29 мин = 3 ч 46мин
Данный пример можно решить двумя способами:
1 способ — складывать часы с часами и минуты с минутами.
4ч. 58мин. + 2ч. 17мин. — 3ч. 29мин.= 3ч. 46мин.
4ч.58мин. + 2ч. 17мин. = 6ч. 75мин.
6ч. 75мин. — 3ч. 29 мин. = 3 ч. 46мин.
2 способ — перевести все часы в минуты.
4ч. 58 мин. = 4*60 + 58 = 298 мин.
2ч. 17мин. = 2*60+17= 137 мин.
3ч.29мин. = 3*60+29 = 209мин.
298 мин.+137 мин. — 209 мин. = 226 мин.
226 мин = 3 ч. 46мин.
Ответ: 3 ч. 46 мин.
б) 18 мин 9 с – 7 мин 46 с + 48 мин 35 с = 58 минут 58 секунд
18 минут 9 секунд — 7 минут 46 секунд
Переводим все в секунды, для этого минуты умножаем на 60 секунд:
18 минут 9 секунд = 1089 секунд
7 минут 46 секунд = 466 секунд
1089—466=623 секунды
623 секунды + 48 минут 35 секунд
48 минут 35 секунд = 2915 секунд
623+2915=3538 секунд
3538 секунд = 58 минут 58 секунд
Ответ: 58 минут 58 секунд
в) 4 мин 52 с · 5 = 24 минуты 20 секунд
Для того чтобы решить данный пример переводим минуты в секунды. В 1 мин — 60 сек. Записываем решение.
4 мин 52 сек = 1 мин × 4 + 52 сек = 60 сек × 4 + 52 сек = 240 сек + 52 сек = 292 сек.
Далее полученное значение подставляем в исходный пример.
4 мин 52 с * 5 = 292 сек × 5 = 1460 сек = 24 мин 20 сек.
В результате получается ответ 24 мин 20 сек.
Ответ: 24 минуты 20 секунд.
г) 7 ч 3 мин : 9 = 47 мин
1час = 60минут
7 * 60 = 420
420 + 3 = 423 мин
423 : 9= 47 мин
Ответ: 47 мин.
10. В вазе лежат персик, ананас и банан. Сколькими различными способами из неё можно взять один, два или три фрукта?
Если взять первые буквы от названий фруктов, то способы перебора можно записать так: ПАБ, ПБА, АПБ, АБП, БАП, БПА. Порядок перебора следующий: каждый из фруктов должен занять первое место в тройках дважды, два других фрукта записываются в любом порядке, а в следующей тройке меняются местами.
Мы рассмотрели случай, когда фрукты берут по одному.
Если можно брать 2 фрукта, тогда возможны такие способы:
ПА и Б
Б и ПА
ПБ и А
А и ПБ
АБ и П
П и АБ.
И еще один способ, если можно взять сразу 3 фрукта из вазы.
Таким образом, мы нашли 6 + 6 + 1 = 13 способов.
Страница 28
1. Составь выражение и найди его значение:
а) Одна ручка стоит 17 р. Сколько надо заплатить за 5 таких ручек?
17 * 5 = 85 (р.) стоят 5 ручек.
Ответ: 85 рублей.
б) Метр ткани стоит 120 р. Сколько стоят 3 м этой ткани?
120 * 3 = 360 (р.) стоит 3 метра ткани.
Ответ: 360 рублей.
в) Литр сока стоит a р. Сколько стоят n л этого сока? Что общего во всех этих задачах? О каких величинах в них идёт речь? Как найти стоимость товара, зная его цену и количество?
Формула стоимости
Пусть C – стоимость товара, a – его цена (то есть стоимость единицы товара – 1 штуки, 1 метра, 1 килограмма, 1 литра и т. д.), а n – количество товара в выбранных единицах. Тогда:
C = a • n
Полученное равенство называется формулой стоимости. Оно означает, что стоимость равна цене, умноженной на количество товара.
Из формулы стоимости по правилу нахождения неизвестного множителя легко выразить величины a и
n : a = C : n
n = C : a
• Цена равна стоимости, делённой на количество товара.
• Количество товара равно стоимости, делённой на цену
2. Найди неизвестные значения величин по формуле стоимости C = a
| С | a | n |
| 360 р. | 60 р/кг | 6 кг |
| 200 р. | 5 р/шт. | 40 шт. |
| 950 р. | 190 р./м | 5 м |
| C | a | n |
| 840 р. | 210 р/шт. | 4 шт. |
| 56 р. | 8 р./л | 7 л |
| 350 р. | 70 р./кг | 5 кг |
3. Цена книги 45 р. Чему равна стоимость 2 книг, 4 книг, 6 книг, n книг? Заполни в тетради таблицу. Запиши формулу зависимости стоимости C купленных книг от их количества n.
| n штук | 2 | 4 | 6 | n |
| С рублей | 90 | 180 | 270 | C = a • n |
Страница 29
4. У Игоря 240 р. Сколько тетрадей он сможет купить, если их цена 10 р., 12 р., 15 р., 20 р., a р.? Заполни таблицу. Запиши формулу зависимости количества купленных тетрадей n от их цены a.
| а р./шт. | 10 | 12 | 15 | 20 | а |
| n шт. | 24 | 20 | 16 | 12 | n = C : a |
5. Реши примеры с комментированием. Найди сумму и разность наибольшего и наименьшего из получившихся чисел:
1. Умножим 85 на 4 единицы, получим 340 единиц.
2. Умножим 85 на 5 десятков, получим 425 десятков. Записываем число 425 со сдвигом на 1 разряд влево.
3. Складываем полученные числа.
Ответ: 4590.
б) 279 • 68 = 18 972
х 279
68
+2232
1674
18972
1. Умножим 279 на 8 единиц, получим 2232 единиц.
2. Умножим 279 на 6 десятков, получим 1674 десятков. Записываем число 1674 со сдвигом на 1 разряд влево.
3. Складываем полученные числа.
Ответ: 18972.
в) 406 • 49 = 19 894
х 406
49
+3654
1624
19894
1. Умножим 406 на 9 единиц, получим 3654 единиц.
2. Умножим 406 на 4 десятка, получим 1624 десятков. Записываем число 1624 со сдвигом на 1 разряд влево.
3. Складываем полученные числа.
Ответ: 19894.
г) 9032 • 97 = 876 104
х 9032
97
+63224
81288
876104
1. Умножим 9032 на 7 единиц, получим 63224 единиц.
2. Умножим 9032 на 9 десятков, получим 81288 десятков. Записываем число 81288 со сдвигом на 1 разряд влево.
3. Складываем полученные числа.
Ответ: 876104.
6. Выполни действия:
х 415
36
+ 2490
1245
14940
б) 709 • 79 = 56 011
х 709
79
+6381
4963
56 011
в) 3705 • 68 = 251 940
х 3705
68
+29640
22230
251940
г) 20 507 • 94 = 1 927 658
7. Мотоциклист выехал из Москвы в Клин со скоростью 45 км/ч. В дороге он сделал две остановки: одну на – 25 мин, а вторую – на 35 мин. В Клин мотоциклист прибыл в 13 ч 20 мин. В котором часу он выехал из Москвы, если расстояние от Москвы до Клина равно 90 км?
1) 25 + 35 = 60 (мин.) — мотоциклист не ехал.
2) 90 : 45 = 2 (ч.) — мотоциклист ехал.
3) 2 + 1 = 3 (ч) — мотоциклист находился в пути.
4) 13 ч 20 мин — 3 ч = 10 ч 20 мин — в это время выехал мотоциклист.
Ответ: выехал в 11 часу.
8. Повтори таблицу мер длины. Используя её, вырази данные величины в указанных единицах измерения:
а)
3 см 5 мм = 35 мм
3 дм 5 см = 35 см
3 дм 5 мм = 305 мм
3 дм 5 см = 350 мм
3 м 5 дм = 3500 см
б)
3 км 5 м = 3 005 м
3 км 5 м = 30 050 дм
3 км 5 м = 300 500 см
3 км 5 м = 3 005 000 мм
3 км 5 см = 3 000 050 мм
9. Выполни действия:
а) (30 км – 5 км 964 м) : 6 = (24 км 36 м) : 6 = 8 км 6 м
б) 40 км 20 м – 78 м 28 мм • 500 = 40 км 20 м — 39 км 14 м = 1 км 6 м
10. Запиши множество делителей и множество кратных числа 21.
11. Расположи 9 элементов в множествах А, В и C так, чтобы в множестве А было 2 элемента, в множестве B – 5 элементов, а в множестве С – 7 элементов. Найди разные варианты решения этой задачи.

Страница 30
1. Выполни умножение с комментированием:
1. Умножим 36 на 9 единиц, получим 324 единиц.
2. Умножим 36 на 7 десятков, получим 252 десятков. Записываем число 252 со сдвигом на 1 разряд влево.
3. Складываем полученные числа.
Ответ: 2844.
1. Умножим 17 на 4 единиц, получим 68 единиц.
2. Умножим 17 на 5 десятков, получим 85 десятков. Записываем число 85 со сдвигом на 1 разряд влево.
3. Складываем полученные числа.
Ответ: 918.
в) 635 • 46 = 29 210
х 635
46
+ 3810
2540
29210
1. Умножим 635 на 6 единиц, получим 3810 единиц.
2. Умножим 635 на 4 десятка, получим 2540 десятков. Записываем число 2540 со сдвигом на 1 разряд влево.
3. Складываем полученные числа.
Ответ: 29210.
г) 281 • 38 = 10678
х 281
38
+2248
843
10678
1. Умножим 281 на 8 единиц, получим 2248 единиц.
2. Умножим 281 на 4 десятка, получим 843 десятков. Записываем число 843 со сдвигом на 1 разряд влево.
3. Складываем полученные числа.
Ответ: 10678.
д) 508 • 75 = 38 100
х 508
75
+ 2540
3556
38100
1. Умножим 508 на 5 единиц, получим 2540 единиц.
2. Умножим 508 на 7 десятков, получим 3556 десятков. Записываем число 3556 со сдвигом на 1 разряд влево.
3. Складываем полученные числа.
Ответ: 38100.
е) 902 • 23 = 20 746
х 902
23
+2706
1804
20746
1. Умножим 902 на 3 единицы, получим 2706 единиц.
2. Умножим 902 на 2 десятка, получим 1804 десятков. Записываем число 1804 со сдвигом на 1 разряд влево.
3. Складываем полученные числа.
Ответ: 20746.
ж) 4205 • 97 = 407 885
х 4205
97
+29435
37845
407885
1. Умножим 4205 на 7 единиц, получим 29435 единиц.
2. Умножим 4205 на 9 десятков, получим 37845 десятков. Записываем число 37845 со сдвигом на 1 разряд влево.
3. Складываем полученные числа.
Ответ: 407885.
з) 9003 • 61 = 549 183
х 9003
61
+ 9003
54018
549183
1. Умножим 9003 на 1 единицу, получим 9003 единиц.
2. Умножим 9003 на 6 десятков, получим 54018 десятков. Записываем число 54018 со сдвигом на 1 разряд влево.
3. Складываем полученные числа.
Ответ: 549183.
2. Найди неизвестные значения величин по формуле стоимости С = а * n
| C | a | n |
| 174 р. | 58 р./м | 3 м |
| 420 р. | 70 р./кг | 6 кг |
| 1000 р. | 50 р./шт. | 20 шт. |
| C | a | n |
| 800 р. | 9 р./кг | 20 кг |
| 450 р. | 50 р./шт. | 9 шт. |
| 1800 р. | 300 р./л | 6 л |
3. Вырази в указанных единицах измерения:
а)
2 км 8 м = 2008 м
2 м 8 см = 208 см
2 дм 8 мм = 208 мм
2 м 8 мм = 2008 мм
б)
2 ч 8 мин = 128 мин
2 сут. 8 ч = 3360 мин
2 т 8 кг = 2008 кг
2 т 8 ц = 2800 кг
4. а) Килограмм клубники стоит 90 р. Сколько рублей надо заплатить за 2 кг такой клубники?
90 * 2 = 180 (р.) — стоит 2 кг клубники.
Ответ: 180 рублей.
б) За 5 одинаковых электронных дисков с играми заплатили 800 р. Сколько рублей стоит один диск?
800 : 5 = 160 (р.) — стоит один диск.
Ответ: 160 рублей.
5. Цена одного билета на поезд равна 800 р. Сколько таких билетов можно купить на 2000 р.? Сколько рублей ещё останется?
2000 : 800 = 2 (ост. 400) (б.) можно купить.
Ответ: 2 билета, 400 рублей.
6. Реши уравнения с комментированием и сделай проверку:
а)
(900 – x : 6) • 5 = 4200
900 – x : 6 = 4200 : 5
900 – x : 6 = 840
x : 6 = 900 — 840
x : 6 = 60
х = 60 * 6
х = 360
б)
325 + (90 – n) : 17 = 330
(90 – n) : 17 = 330 — 325
(90 – n) = 5 * 17
90 – n = 85
n = 90 — 85
n = 5
7. В строке 56 печатных знаков, а на странице – 36 строк. Сколько печатных знаков уместится на 64 страницах?
1) 56 * 36 = 2016 (з.) — поместится на странице.
2) 2016 * 64 = 129 024 (з.) — поместится н 64 страницах.
х 2016
64
+ 8064
12096
129024
Ответ: 129 024 знака
8. а) Поезд шёл 18 ч со скоростью 76 км/ч и 16 ч со скоростью 72 км/ч. Какое расстояние прошёл поезд за всё это время?
1) 76 * 18 = 1368 (км) — поезд прошел со скоростью 76 км/ч.
2) 72 * 16 = 1152 (км) — прошел скоростью 72 км/ч.
3) 1368 + 1152 = 2520 (км) — прошел поезд.
Ответ: 2520 км.
б) Почтальон проехал на велосипеде 36 км за 2 ч. Затем он уменьшил скорость на 2 км/ч и ехал ещё 3 ч. Сколько всего километров проехал на велосипеде почтальон?
1) 36 : 2 = 18 (км/ч) — была скорость почтальона.
2) 18 — 2 = 16 (км/ч) — стала скорость почтальона.
3) 169 * 3 = 48 (км) — проехал со скоростью 16 км/ч.
4) 36 + 48 = 84 (км) — всего проехал почтальон.
Ответ: 84 км.
9. Почтовый голубь должен доставить донесение на расстояние 130 км. Скорость голубя 50 км/ч. Успеет ли он доставить это донесение: а) за 2 часа? б) за 3 часа?
За 2 часа успеет, за 3 нет.
Страница 31
10. Запиши предложение в виде равенства:
а) n на 17 меньше, чем m
б) x в 8 раз меньше, чем y
в) a на 92 меньше, чем b
г) k в 5 раз больше, чем d
11. Продолжительность дня равна t ч. Чему равна продолжительность ночи? Составь выражение и найди его значение, если t = 8, 10, 12. Какие значения может принимать переменная t?
t = 8, 24 — 8 = 16 ч.
t = 10, 24 — 10 = 14 ч.
t = 12 24 — 12 = 12 ч.
12. Запиши программу действий в виде выражения со скобками. Найди значение полученного выражения.
(2488 + 4512) * 593 − (485830 − 37598) : 8 = 7000 * 593 − 448232 : 8 = 4151000 − 56029 = 4094971
13. Реши уравнения устно. Расположи ответы в порядке возрастания. Расшифруй имя сказочного героя. Узнай название книги и имя её автора.
М 9 + b = 12 b = 3
А 52 : t = 13 t = 4
Т a · 50 = 250 a = 5
Р 34 – x = 17 х = 17
О 90 : d = 5 d = 18
C 40 – c = 12 c = 28
К n – 2 7 = 8 n = 35
И 8 • m = 480 m = 60
Н k : 19 = 4 к = 76
МАТРОСКИН из ПРОСТОКВАШИНО, автор Эдуард Успенский.
14. Запиши множество делителей и множество кратных числа 22.
15. В классе 25 учеников. Им было предложено заниматься в двух кружках: по математике и рисованию. В каждый кружок записалось по 16 человек, причём 10 человек – в оба кружка одновременно. Узнав результаты, ребята удивились: «Можно подумать, что в нашем классе не 25 учеников, а все 42!» Но один любитель математики сказал: «Вовсе нет! У нас даже несколько ребят не записались ни в один из этих кружков!»
Докажи, что он прав. Сколько таких ребят?
1) 16 – 10 = 6 (уч.) – занимаются только математикой и только окружающим миром,
2) 6 + 10 + 6 = 22 (уч.) – занимаются в данных кружках,
3) 25 – 22 = 3 (уч.) – не занимаются в данных кружках.
Ответ: 3 ученика не занимаются, значит любитель математики прав.
Страница 32
1. а) Что общего в выражениях? Вспомни правило умножения круглых чисел и вычисли:
400 • 70 = 4 * 7 * 1000 = 28000
160 • 300 = 16 * 3 * 1000 = 48 000
9 • 80 000 = 9 * 8 * 10 000 = 720 000
250 • 4000 = 25 * 4 * 10 000 = 1 000 000
б) Как записывают умножение круглых чисел в столбик? Почему? Приведи свой пример.
Записывают так, чтобы не умножать на ноли в конце числа, но после их учитывают в результате.
2. Выполни действия:
х 360
7500
+180
252
2700000
б) 2800 • 940 = 2 632 000
х 2800
940
+112
252
2632000
в) 50 900 • 62 = 3 155 800
х 62
50900
+ 558
310
3155800
г) 73 050 • 8600 = 623 230 000
3. Вычисли. Расположи ответы в порядке убывания. Расшифруй имя короля сказочного государства, который избавил детей от скучных занятий в школе. Узнай название этой книги и имя её автора.
4. Составь программу действий и вычисли:
2 5 3 4 1
а) 860 • 900 – 6750 : 5 • (24 + 44) = 682 200
1) 24 + 44 = 68
2) 860 * 900 = 774 000
х 860
900
774000
4) 1350 * 68 = 91800
х 1350
68
+1080
810
91800
5) 774 000 — 91 800 = 682 200
— 774000
91800
682200
1 2 3 5 4
б) (64 + 137) • 28 • 910 – 560 772 : 9 = 5 059 172
1) 64 + 137 = 201
2) 201 * 28 = 5 628
3) 5 628 * 910 = 5 121 480
х 5628
910
+ 5628
50652
5121480
4) 560772 : 9 = 62 308
5) 5 121 480 — 62 308 = 5 059 172
5. Сравни в каждом равенстве числа, обозначенные буквами. Какое из них больше, а какое меньше? На сколько?
a = b + 18 a > b
k – t = 5 k > t
x = y – 9 x < y
n – 4 = m n > m
Страница 33
6. Реши уравнения с комментированием и сделай проверку:
а)
(k : 16) • 13 + 11 = 50
(k : 16) • 13 = 50 — 11
(k : 16) • 13 = 39
k : 16 = 39 : 13
k : 16 = 3
k = 3 * 16
k = 48
Проверка:
(48 : 16) • 13 + 11 = 50
50 = 50
б)
14 – 72 : (d – 3) = 8
72 : (d – 3) = 14 — 8
72 : (d – 3) = 6
d – 3 = 72 : 6
d – 3 = 12
d = 15
Проверка:
14 – 72 : (15 – 3) = 8
8 = 8
7. а) Одна роза стоит 40 р. Сколько надо заплатить за букет из 7 роз?
40 * 7 = 280 (р.) — стоит букет роз.
Ответ: 280 рублей.
б) Одна конфета стоит 12 р. Сколько таких конфет можно купить на 60 рублей?
60 : 12 = 5 (к.) можно купить.
Ответ: 5 конфет.
в) За 20 календарей заплатили 1800 р. Сколько рублей стоит один календарь?
1800 : 20 = 90 (р.) — стоит календарь.
Ответ: 90 рублей.
8. За футболку и 4 пары носков заплатили 200 рублей. Футболка стоит 80 р. Сколько рублей стоит одна пара носков?
1) 200 = 80 = 120 (р.) — стоит 4 пары носков.
2) 120 : 4 = 30 (р.) — стоит пара носков.
Ответ: 30 рублей.
9. У Оли было 200 р. Она купила 3 тетради по цене 15 р., 2 ручки по 37 р. и 6 карандашей по 8 р. Сколько денег у неё осталось? Сможет ли она купить на них шоколадку за 32 р.?
1) 15 * 3 = 45 (р.) — стоили тетради.
2) 37 * 2 = 72 (р.) стоили ручки.
3) 8 * 6 = 48 (р.) — стоили карандаши.
4) 45 + 72 + 48 = 165 (р.) — стоила покупка.
5) 200 — 165 = 35 (р.) — осталось.
32 < 35 — да сможет купить шоколадку.
Ответ: осталось 35 рублей. Сможет купить шоколадку.
10. Запиши множество делителей и множество кратных числа 23.
11. Масса первого арбуза равна a кг. Масса второго арбуза – на 3 кг меньше массы первого. А масса третьего арбуза – в 2 раза больше массы второго. Чему равна масса трёх арбузов вместе? Составь выражение и найди его значение при a = 8.
Составляем выражение
a + (a — 3) + (a — 3) * 2
При а = 8
8 + (8 — 3) + (8 — 3) * 2 = 8 + 5 + 10 = 23 (кг) масса арбузов.
Ответ: 23 кг.
12. Тарас бежит со скоростью 150 м/мин, а Юра – со скоростью 12 км/ч. Кто из них бежит быстрее?
150 : 1000 * 60 = 9000 : 1000 = 9 (км/ч) скорость Тараса.
9 < 12 Тарас бежит медленнее.
Ответ: Юра быстрее.
13. Записано подряд семь семёрок. Найди такой способ расстановки скобок и знаков арифметических действий, чтобы значение полученного выражения было равно 7. Какие ещё значения выражений могут при этом получаться? Как ты думаешь, в каком случае значение полученного выражения будет наибольшим?
Наибольшее значение: 777 • 7777 = 6042729
1. Прочитай задачу и объясни, как составлена таблица. Составь план решения задачи и найди ответ.
«Месяц назад 2 одинаковые порции мороженого стоили 36 р. Сейчас его цена увеличилась на 2 р. Сколько теперь надо заплатить за 5 таких порций мороженого?»
| C | a | n | |
| Раньше | 36 р. | 18 р./шт. | 2 шт. |
| Сейчас | 100 р. | 18 + 2 = 20 р./шт. | 5 шт. |
1) 36 : 2 = 18 (р.) — стоило мороженое.
2) 18 + 2 = 20 (р.) — стоит мороженое сейчас.
3) 20 * 5 = 100 (р.) — стоит 5 мороженных.
Ответ: 100 рублей.
2. Реши задачи с помощью таблиц:
а) Маша купила 7 заколок, а Вера – на 2 заколки меньше. Цена всех заколок одинаковая. Маша заплатила на 140 р. больше Веры. Сколько стоит одна заколка? Сколько рублей заплатила за заколки каждая из девочек?
| C | a | n | |
| М | 490 р. | 70 р./шт. | 7 шт. |
| В | 350 р. | 5 шт. | |
| М — В | 140 р. | 2 шт. |
б) Саша и Дима купили вместе 20 солдатиков по одинаковой цене. Саша заплатил 720 р., а Дима – на 240 р. меньше. Сколько солдатиков купил каждый из них?
| C | a | n | |
| с | 720 р. | 60 р./шт. | 12 шт. |
| д | 720-240 р. | 8 шт. | |
| с + д | 1200 р. | 20 шт. |
3. а) 9 пирожных, имеющих одну цену, стоят 234 р. Сколько рублей надо заплатить за 7 таких пирожных?
1) 234 : 9 = 26 (р.) — стоит пирожное.
2) 26 * 7 = 182 (р.) — стоит 7 пирожных.
Ответ: 182 рубля.
б) Мама сначала купила 3 кг яблок по цене 40 р. за килограмм, а потом ещё 2 кг таких же яблок. Сколько денег она заплатила?
1) (3 + 2) * 40 = 5 * 40 = 200 (р.) — заплатила мама.
Ответ: 200 рублей.
4. Для осенних посадок купили 60 пакетов луковиц тюльпанов по цене 15 р. за пакет, а нарциссов – на 25 пакетов меньше. Цена пакета нарциссов на 3 р. меньше, чем цена пакета тюльпанов. Сколько рублей надо заплатить за всю эту покупку?
1) 60 * 15 = 900 (р.) — стоили тюльпаны.
2) 60 — 25 = 35 (п.) — купили нарциссов.
3) 15 — 3 = 12 (р.) — стоит пакетик нарциссов.
4) 35 * 12 = 420 (р.) — стоят нарциссы.
5) 420 + 900 = 1320 (р.) — стоит покупка.
Ответ: 1320 рублей.
Страница 35
5. Вычисли устно наиболее удобным способом:
а) 126 + 99 = 125 + 100 = 225
д) 997 • 452 + 3 • 452 = 452 * (997 + 3) = 452 * 1000 = 452 000
б) 532 – 98 = 530 — 100 + 2 + 2 = 434
е) 284 + 98 + 116 + 2 = 400 + 100 = 500
в) 20 • 142 • 5 = 142 * 100 = 14 200
ж) (939 + 56) – 239 = 939 — 239 + 56 = 700 + 56 = 756
г) 73 • 25 • 4 = 73 * 100 = 7 300
з) 721 – 96 – 621 = 100 — 96 = 4
6. Выполни умножение:
х 450
7600
+ 270
315
3420000
б) 58 000 • 4700 = 272 600 000
х 58000
4700
+ 406
232
272600000
в) 20 560 • 950 = 19 532 000
х 20560
950
+ 10280
18504
19532000
г) 69 • 300 800 = 20 755 200
х 300800
69
+27072
18048
20755200
7. Реши уравнения с комментированием и сделай проверку:
а) (980 : n) • 18 – 84 = 276
(980 : n) • 18 = 276 + 84
(980 : n) = 360 : 18
980 : n = 20
n = 980 : 20
n = 49
Проверка:
(980 : 20) • 18 – 84 = 276
276 = 276
б) 96 + (80 – x) : 14 = 100
(80 – x) : 14 = 100 — 96
80 – x = 4 * 14
80 – x= 56
х = 80 — 56
х = 24
Проверка:
96 + (80 – 24) : 14 = 100
100 = 100
8. По рисунку найди делимое, делитель, частное и остаток. Запиши соотношение между ними с помощью формулы a = b • c + r, r < b. Проверь записанное равенство с помощью вычислений.
9. Запиши множество делителей и множество кратных числа 24.
10. Сравни в каждом равенстве числа, обозначенные буквами. Какое из них больше, а какое меньше? На сколько?
n = m • 3 — m < n в 3 раза
c • 10 = d — c < d в 10 раз
k : t = 2 — k > t в 2 раза
a : b = 6 — a > b в 6 раз
p : 5 = r — p > r в 5 раз
y = x : 8 — y < x в 8 раз
11. Длина класса, имеющего форму прямоугольного параллелепипеда, равна 12 м, ширина – 8 м, а высота – 4 м. Найди объём этого класса, площадь его пола, потолка, стен.
1) 8 * 4 = 32 (м 2 ) — площадь каждой из двух стен по ширине.
2) 12 * 4 = 48 (м 2 ) — площадь каждой из двух других стен по длине.
3) 12 * 8 = 96 (м 2 ) — площадь пола или потолка.
4) 96 * 4 = 384 (м 3 ) — объем класса.
Ответ: площадь стен 32 м 2 , 48 м 2 , потолка или пола 96 м 2 , объем 384 м 3 .
12. Какие из прямоугольных параллелепипедов A, B, C, D, E могут иметь данную на рисунке развёртку?
Страница 36
1. Выполни действия:
х 916
73
+2748
6412
66868
б) 850 • 3800 = 3 230 000
х 850
3800
+ 680
255
3230000
в) 20 900 • 9400 = 196 460 000
х 20900
9400
+ 836
1881
196460000
г) 60 080 • 460 = 27 636 800
2. Придумай задачи по таблицам и реши их с помощью формулы стоимости:
1. Мама купила в магазине 5 пирожков по 46 рублей и 8 булочек по 27 рублей. На сколько больше мама заплатила за пирожки, чем за булочки?
1) 46 * 5 = 230 (р.) — стоили пирожки.
2) 27 * 8 = 216 (р.) — стоили булочки.
3) 230 — 216 = 14 (р.) — на столько дороже были пирожки, чем булочки.
Ответ: на 14 рублей.
2. Мама купила 6 пирожков за 192 рубля и 4 пирожных за 384 рубля. во сколько раз пирожное дороже пирожка.
1) 192 : 6 = 32 (р.) — стоит пирожок.
2) 384 : 4 = 64 (р.) — стоит пирожное
3) 64 : 32 = 2 (раза) — во столько дороже пирожное.
Ответ: 2 раза.
а) Мама купила 3 м шёлка по a р. за метр и 5 м ситца по b р. за метр. Сколько рублей она заплатила за всю покупку?
б) Цена конфеты n р. Вадим купил 6 таких конфет, и у него ещё осталось t р. Сколько денег у него было вначале?
в) Саше надо купить 7 бубликов по k р. за штуку. В кассу он отдал y р. Сколько сдачи он должен получить?
г) Цена арбуза a р. за килограмм, а дыни – b р. за килограмм. На сколько рублей дыня массой в 5 кг дороже арбуза массой 6 кг?
4. У Алёши в кошельке 6 монет по 5 р., две монеты по 10 р. и одна купюра 50 р. Он купил 3 тетради по цене 18 р., ластик за 12 р. и линейку за 19 р. На оставшиеся деньги он решил купить ластики. Сколько ластиков он сможет купить, если их цена 5 р. за штуку?
1) 5 * 6 + 10 * 2 + 50 = 100 (р.) — было у Алеши.
2) 18 * 3 + 12 + 19 = 79 (р.) — потратил на покупку.
3) 100 — 79 = 21 (р.) — осталось.
4) 21 : 5 = 4 (ост. 1) (л.) — сможет купить.
Ответ: 4 ластика.
5. Реши уравнения с комментированием и проверкой:
а) (24 – 360 : x) · 6 = 90
24 – 360 : x = 90 : 6
360 : x = 24 — 15
360 : x = 9
х = 360 : 9
х = 40
Проверка:
(24 – 360 : x) · 6 = 90
90 = 90
б) 4 + (у – 14) : 3 = 20
(у – 14) : 3 = 20 — 4
у – 14 = 16 * 3
у = 48 + 14
у = 62
Проверка:
4 + (у – 14) : 3 = 20
20 = 20
Страница 37
6. Сравни в каждом равенстве числа, обозначенные буквами:
n – 8 = d n > d
p = t + 9 p > t
a – k = 2 a > k
c : b = 8 c > b
x • 5 = y x < y
r = m : 7 m > r
7. Вырази величины в указанных единицах измерения:
а)
4 км 25 м = 4025 м
4 м 25 см = 425 см
4 м 25 мм = 4025 мм
4 м 2 25 дм 2 = 425 дм 2
4 дм 3 25 см 3 = 64 025 см 3
б)
4 ц 25 кг = 425 кг
4 т 25 кг = 4025 кг
4 кг 25 г = 4025 г
4 ч 25 мин = 265 мин
4 мин 25 с = 265 с
8. Вычисли. Расположи ответы в порядке убывания и расшифруй слово. Найди в словаре, что оно означает. Припомни, а с тобой это случалось?
К 4900 * 507 = 2 484 300
У 3008 * 720 = 2 165 760
Р 890 * 480 = 427 200
Ё 892 * 53 = 47 276
Ь 2070 * 92 = 190 440
З 570 * 75 = 42 750
9. Запиши множество делителей и множество кратных числа 25.
10. Набери указанную сумму денег наименьшим возможным числом монет и купюр. Составь и заполни таблицу в тетради.
| сумма в рублях | Монет и купюр | Всего монет и купюр | ||||||
| 500 | 100 | 50 | 10 | 5 | 2 | 1 | ||
| 298 | — | 2 | 1 | 4 | 1 | 1 | 1 | 10 |
| 364 | — | 3 | 1 | 1 | — | 2 | 1 | 7 |
| 472 | — | 4 | 1 | 2 | — | 1 | — | 8 |
| 725 | 1 | 2 | — | 2 | 1 | — | — | 6 |
| 1056 | 2 | — | 1 | — | 1 | — | 1 | 5 |
| 2939 | 5 | 4 | — | 3 | 1 | 2 | — | 15 |
11. Подбери корни уравнений. Обоснуй свой ответ.
а) x + x + x + x = 4 • 752
У нас 4 штуки х, значит 4 * х, а в правой части 4 * 752, значит х = 752. Проверим:
4х = 3008
х = 3008 : 4
х = 752
б) (y + 7) • 5 = 8 • 5 + 7 • 5
Вынесем за скобки 5 из правой части, получится (8+7)*5, значит у = 8. Проверим:
(y + 7) • 5 = 40 + 35
(y + 7) • 5 = 75
y + 7 = 75 : 5
y + 7= 15
у = 8
12. Одно из чисел увеличили в 12 раз, а другое уменьшили в 3 раза. Как изменилось произведение этих чисел?
Можно записать в виде выражения. a * 12 * b : 3 = a * 4 * b То есть их произведение увеличилось в 4 раза.
Страница 38
1. а) Объясни по рисунку, как умножить число на сумму, и выполни умножение:
а • (b + c + d) = a • b + a • c + a • d
Можно вынести за скобки общий множитель, а числа сложить между собой
156 • 324 = 156 • (300 + 20 + 4) = 156 * 324 = 50 544
б) Используя рисунок, объясни способ записи умножения на трёхзначное число в столбик:
Умножаем отдельно единицы, десятки, сотни и т.д, при этом результаты складываем, смещая их при сложении столбиком на один разряд влево.
2. В одной упаковке 248 ластиков. Сколько ластиков в 536 упаковках? Найди ответ в данной записи примера. Можно ли по этой записи определить, сколько ластиков в 6 упаковках, в 30 упаковках, в 500 упаковках, в 5360 упаковках?
Найти сколько ластиков в 6 упаковках, в 30 упаковках, в 500 упаковках, в 5360 упаковках можно выбирая значения из умножения столбиком.
Так для 30 упаковок это 744 десятка, то есть 7 440.
Для 500 упаковок 1240 сотен, то есть 124 000.
Для 5360 надо результат умножить на 10 или добавить в конце ноль, то есть 1 329 280
Страница 39
3. За вод за один день выпускает 485 автомобилей. На какие вопросы можно ответить по данной записи примеров?
Сколько выпускает за 5 дней, за 6 дней, за 60 дней, за 300 дней.
Можно ли, не вычисляя, сказать, на сколько второе произведение больше первого?
Да, можно. На 485, так как в левом примере 485 взято 365 раз, а в правом 366.
4. Найди значения выражений:
х 752
128
+6016
1504
752
96256
б) 246 • 496 = 122 016
х 246
496
+1476
2214
984
122016
в) 405 • 527 = 213 435
х 405
527
+ 2835
910
2025
213435
г) 906 • 358 = 324 348
х 906
358
+ 7248
4530
2718
324348
д) 1029 • 374 = 384 846
х 1029
374
+ 4116
7203
3087
384846
е) 8503 • 982 = 8 349 946
х 8503
982
+ 17006
68024
76527
8349946
ж) 5007 • 716 = 3 585 012
х 5007
716
+ 30042
5007
35049
3585012
з) 30 209 • 245 = 7 401 205
х 30209
245
+ 151045
120836
60418
7401205
5. Вычисли. Расшифруй слово, расположив ответы примеров в порядке возрастания. Кто это? Найди информацию о нём в Интернете или энциклопедии.
Б 2580 * 27 = 69 660
Е 364 * 214 = 77 896
Р 706 * 329 = 232 274
К 569 * 456 = 259 464
У 508 * 652 = 331 216
Т 47045 * 84 = 3 951 780
БЕРКУТ — хищная птица семейства ястребиных, самый крупный орёл.
6. Реши уравнения и сделай проверку:
а)
62 – (116 + x) : 5 = 34
(116 + x) : 5 = 62 — 34
(116 + x) : 5 = 28
116 + x = 28 * 5
х = 140 — 116
х = 24
Проверка:
62 – (116 + 24) : 5 = 34
34 = 34
б) 540 : (y • 3 – 60) = 6
y • 3 – 60 = 540 : 6
y • 3 – 60 = 90
y • 3 = 150
y = 150 : 3
у = 50
Проверка:
540 : (50 • 3 – 60) = 6
6 = 6
а) Олег съел n пирожков, а Саша – на 3 пирожка меньше. Во сколько раз меньше пирожков съел Саша, чем Олег?
б) У Маши b марок, а у Гены в 5 раз меньше. Сколько марок у них вместе?
в) Аня шла 2 ч со скоростью x км/ч, а Поли на – 4 ч со скоростью y км/ч. На сколько километров больше прошла Полина, чем Аня?
г) В вазе было c груш. Из неё взяли 6 раз по d груш. Сколько груш осталось в вазе?
д) Три одинаковые конфеты стоят k р. Сколько рублей надо заплатить за 8 таких конфет?
Страница 40
8. а) Поезд прошёл расстояние 560 км со скоростью 70 км/ч, а расстояние 240 км – со скоростью 60 км/ч. Сколько времени он был в пути?
1) 560 : 70 = 8 (ч.) — поезд ехал со скоростью 70 км/ч.
2) 240 : 60 = 4 (ч.) — поезд ехал со скоростью 60 км/ч.
3) 8 + 4 = 12 (ч.) — ехал поезд.
Ответ: 12 часов.
б) Для спортивного зала купили на 560 р. резиновые мячи по цене 70 р. за штуку и на 240 р. теннисные мячи по цене 60 р. за штуку. Сколько всего мячей купили? Что ты замечаешь?
1) 560 : 70 = 8 (м.) — купили по 70 р.
2) 240 : 60 = 4 (м.) — купили по 60 р.
3) 8 + 4 = 12 (м.) — всего купили.
Ответ: 12 мячей.
Придумай свою задачу с другими величинами, которая решается так же
Автомобиль проехал 560 км со скорость 70 км/ч, а мотоциклист 240 км, со скоростью 60 км/ч. Сколько часов в пути был мотоцикл и автомобиль.
1) 560 : 70 = 8 (ч.) — ехал автомобиль.
2) 240 : 60 = 4 (ч.) — ехал мотоциклист.
3) 8 + 4 = 12 (ч.) — ехали мотоцикл и автомобиль.
Ответ: 12 часов.
9. Выполни вычисления по алгоритму, заданному блок схемой. Составь и заполни таблицу в тетради
| a | 1 | 3 | 5 | 7 | 9 | 11 |
| x | 0 | 0 | 5 | 7 | 9 | 11 |
| a | 1 | 3 | 5 | 7 | 9 | 11 |
| x | 1 | 3 | 0 | 0 | 0 | 0 |
10. Сравни, не вычисляя:
352 • 218 = 218 • 352
920 • 614 = 614 • 920
516 • 724 < 724 • 521
306 • 825 > 294 • 438
368 : 8 >368 : 23
504 : 56 < 672 : 56
11. Повтори римскую нумерацию (ч. 1, с. 62).
а) Запиши арабскими цифрами числа: VII, IX, XXIV, XLVI, CCCIV, DCCXII, MLVI.
б) Запиши римскими цифрами числа: 4, 11, 36, 59, 93, 125, 408, 2002
IV, XI, XXXVI, LIX, XCIII, CXXV, CDVIII, MMII
12. В одной книге указан та кой год издания: МDCCXLIX. Когда издана эта книга?
Страница 41
1. Рассмотри два способа умножения на трёхзначное число, в разряде десятков которого стоит 0. Чем отличаются эти способы? Почему в практике вычислений обычно используется второй способ?
2. Найди значения произведений:
а) 963 • 407 = 391 941
в) 529 • 104 = 55 016
д) 807 • 307 = 247 749
ж) 402 • 609 = 244 818
б) 216 • 809 = 174 744
г) 745 • 902 = 671 990
е) 201 • 508 = 102 108
з) 905 • 106 = 95 930
3. Вычисли. Расшифруй название старинной единицы объёма сыпучих тел во Франции. Узнай, скольким литрам она примерно равна.
МЮИД
* мюид — а, м. muid <лат. modius. Старинная единица объема жидкостей и сыпучих тел во Франции (около 270 л.)
4. Найди значение выражения 527 • a, если a = 48, 250, 673, 901.
х527
250
+2635
1054
131750
х527
673
+1581
3689
3162
354671
5. Реши задачи и сравни их. Что ты замечаешь?
а) Слава бежал 3 мин со скоростью 200 м/мин. Затем он увеличил скорость на 40 м/мин и бежал ещё 2 мин. После этого ему осталось пробежать 120 м. Сколько всего метров надо пробежать Славе?
1) 3 * 200 = 600 (м) — пробежал за первые 3 минуты
2) 200 + 40 = 240 (м/мин) — стала скорость после 3 минут
3) 240 * 2 = 480 (м) — пробежал после 3 минут.
4) 600 + 480 +120 = 1200 (м) — надо пробежать.
Ответ: 1200 метров.
б) Блузка стоит 200 р., а юбка – на 40 р. дороже. Нина купила 3 блузки и 2 юбки, и после этого у неё осталось 120 р. Сколько денег было у Нины вначале? Придумай ещё какую-нибудь задачу, которая решается так же.
1) 200 * 3 = 600 (р.) — стоят 3 блузки.
2) 200 + 40 = 240 (р.) — стоит юбка.
3) 240 * 2 = 480 (р.) — стоит 2 юбки.
4) 600 + 480 +120 = 1200 (р.) — было денег.
Ответ: 1200 рублей.
* Токарь выточил за 3 часа 200 деталей, за следующие 2 часа на 40 деталей больше каждый час. И до конца смены ему по плану осталось выточить 120 деталей. Сколько деталей надо выточить токарю по плану?
6. Запиши множество делителей и множество кратных числа 26.
Ответы к странице 42
7. Выполни действия:
а) 4 дм 5 см + 3 м 7 см = 45 см + 307 см = 352 см = 3 м 5 дм 5 см
б) 5 км 32 м + 4 км 756 м = 5032 м + 4756 м = 9788 м
в) 7 дм2 6 см2 + 18 дм2 68 см2 = 706 см2 + 1868 см2 = 2574 см2 = 25 дм2 74 см2
г) 8 т 96 кг – 429 кг = 8096 кг — 429 кг = 7 667 кг = 7 т 667 кг
д) 6 ч 32 мин + 19 ч 58 мин = 25 ч + 30 мин + 2 мин + 58 мин = 26 ч 30 мин
е) 40 мин 2 с – 34 мин 25 с = 39 мин + 1 мин + 2 с — 34 мин — 25 с = 5 мин + 2 с + 1 мин — 25 с = 5 мин + 2 с + 35 с = 5 мин 37 с
8. Игра «Кто какое число задумал?»
а) Зайка-попрыгайка задумал число, прибавил его к числу 26, сумму умножил на 5 и из полученного произведения вычел 42. В результате у него получилось 138. Какое число задумал Зайка-попрыгайка?
Решим задачу с помощью уравнения. Пусть x — число, которое задумал кот Матроскин.
Потом он добавил 26 и получил: х + 26. Сумму умножил на 5, ( х + 26 ) * 5. Далее вычел 42, ( х + 26 ) * 5 — 42. Составим и решим уравнение, зная что кот Матроскин получил 138:
( х + 26 ) * 5 — 42 = 138,
5 * х + 130 — 42 = 138,
5 * х = 138 — 130 + 42,
5 * х = 50,
х = 50 : 5,
х = 10.
Ответ: Кот Матроскин задумал число 10.
б) Мышка-норушка вычла задуманное число из 31, разность разделила на 9 и к полученному результату прибавила 8. В ответе у неё получилось 11. Какое число задумала Мышка-норушка?
Составим уравнение, где х- задуманное число
(31-х)/9+8=11
(31-х)/9=11-8
(31-х)/9=3
31-х=3*9
31-х=27
х=31-27
х=4
Ответ: Мышка-норушка задумала 4.
в) Лягушка-квакушка разделила 250 на заду-манное число, вычла из частного 24 и разность умножила на 2. В результате у неё получилось 52. Какое число задумала Лягушка-квакушка?
Составим уравнение, где х- задуманное число
(250 : x — 24) • 2 = 52
250 : х — 24 = 52 : 2
250: х-24 = 26
250:х = 26 + 24
250 : х = 50
x = 250 : 50
x = 5
Ответ: число 5 загадал Дядя Фёдор.
9. Составь программу действий и вычисли:
2 5 3 6 1 4
72 • 480 + 789 • 295 – (34 188 + 392 012) : 100 = 263 053
4) 426200 : 100 = 4262
5)
+ 34560
232755
267315
6)
-267315
4262
263053
10. Начерти пятиугольник ABCDE и проведи прямую 1 так, чтобы она разбила пятиугольник:
а) на треугольник и шестиугольник;
б) на треугольник и пятиугольник;
в) на четырёхугольник и пятиугольник;
г) на два четырёхугольника.
11. Какой из прямоугольных параллелепипедов, изображённых на рисунке, вместительнее?
Найдем объемы и узнаем какой вместительнее.
1) 87*56*43 = 4872 * 43 = 209496 (см 3 ) — объем левого параллелепипеда.
х4872
43
+ 14616
19488
209496
2) 62*62*62 = 3844 (см 3 ) — объем правого параллелепипеда.
Ответ: левый параллелепипед по объему больше.
12. Найди площадь поверхности куба, объём которого равен 64 см 3
Школьники в 3 классе не проходят корни, тем более кубические, поэтому первая операция фактически должна выполняться подбором.
1) 4 * 4 * 4 = 64 из этого можно сделать вывод, что ребро квадрата равна 4 см.
2) 4 * 4 = 16 (см 3 ) — площадь грани.
3) 16 * 6 = 96 (см 2 ) — площадь поверхности куба.
Ответ: 96 см 2 .
13. Что больше: треть половины или половина трети числа? Обоснуй свой ответ.
Треть половины это 1/2 * 1/3 , то есть 1/6
Половина трети это 1/3 * 1/2, то есть 1/6
Получается в итоге, что эти части равны.
14. У Димы было 8 кусочков бумаги. Некоторые из них он разрезал на 3 части, и у него стало 20 кусочков. Сколько кусочков разрезал Дима?
1) 20 — 8 = 12 (к.) — добавилось.
2) 12 : 2 = 6 (к.) — надо разрезать, чтобы из них стало 12.
Ответ: 12 кусочков разрезал.
Ответы к странице 43
1. Найди ошибки в записи и решении примеров:
Запиши и реши их в тетради правильно.
2. Выполни действия:
а) 318 • 956 = 304008
б) 729 • 304 = 221616
в) 407 • 501 = 203907
г) 60 080 • 264 = 15 861 120
3. Запиши формулу стоимости. Используя её, заполни таблицу:
| C, р. | 552 | 840 | 6300 | 1000 | 8500 | 3600 |
| a р./шт. | 92 | 168 | 90 | 25 | 500 | 30 |
| n шт. | 6 | 5 | 70 | 40 | 17 | 120 |
4. Для букета купили 5 роз и 6 гербер. Каждая роза стоит 45 р., а гербера – в 3 раза дешевле. Сколько рублей стоит весь букет?
1) 45 : 3 = 15 (р.) — стоит гербер.
2) 5 * 45 = 225 (р.) — стоят розы.
3) 6* 15 = 90 (р.) — стоят герберы.
4) 225 + 90 = 315 (р.) — стоит букет.
Ответ: 315 рублей.
5. Стол и 4 одинаковых стула стоят 2800 р. За стол заплатили 1200 р. Сколько рублей стоит один стул?
1) 2800 — 1200 = 1600 (р.) — стоят стулья.
2) 1600 : 4 = 400 (р.) — стоит стул.
Ответ: 400 рублей.
6. а) Составь выражение к задаче: «Расстояние от Бреста до Киева примерно 600 км. Поезд ехал из Бреста в Киев сначала 2 ч со скоростью 60 км/ч, а потом t ч со скоростью 80 км/ч. Сколько километров ему осталось проехать?» Найди значение выражения при t = 1, 2, 3, 4, 5, 6. Может ли t принять значение, равное 10
б) Пусть d км – расстояние, оставшееся до Киева. Заполни таблицу и составь формулу зависимости d от t:
| t ч | 0 | 1 | 2 | 3 | 4 | 5 | 6 | t |
| d км | 480 | 400 | 320 | 240 | 160 | 80 | 0 | d = 480 — 80 * t |
Ответы к странице 44
7. Автобус проехал 180 км за 4 часа, а обратный путь – на 1 час быстрее. На сколько километров в час увеличилась скорость автобуса на обратном пути?
1) 180 : 4 = 45 (км/ч) — была скорость автобуса.
2) 180 : 3 = 60 (км/ч) — стала скорость автобуса.
3) 60 — 45 = 15 (км/ч) — на столько скорость увеличилась на обратном пути.
Ответ: на 15 км/ч.
8. (Устно.) Подбери корни уравнений или объясни, почему их нет. Сделай проверку:
n – 0 = 7
n = 7 + 0
n = 7
a – a = 7
нет корней
t – 7 = 0
t = 0 + 7
t = 7
а) За 5 банок краски заплатили k р., а за 9 банок лака – n р. На сколько рублей банка краски дороже банки лака?
б) Три рюкзака стоят а р., а две палатки – на b р. дороже. На сколько рублей рюкзак дешевле палатки?
в) Пешеход прошёл d км за 4 часа. Скорость велосипедиста – на m км/ч больше. С какой скоростью ехал велосипедист?
г) Лодка проплыла s км за 5 ч, а катер это же расстояние – за 2 ч. На сколько километров в час скорость катера больше скорости лодки?
10. Выполни действия:
а) 985 468 + 45 032 = 1 030 500
б) 507 000 – 92 944 = 414056
в) 8000 • 8090 = 64 720 000
г) 4 905 600 : 70 = 70 080
11. Какие точки на рисунке принадлежат прямой l, а какие – не принадлежат? Запиши в тетради, используя знаки принадлежит и не принадлежит.
12. Пусть A – множество делителей числа 18, а B – множество делителей числа 27. Запиши множества A и B с помощью фигурных скобок. Найди их пересечение. Назови наибольший общий делитель чисел 18 и 27
Страница 45
1. Вале и Гале было поручено сделать флажки для ёлки. Валя сделала за 2 часа 40 флажков, а Галя за 3 часа – 45 флажков. Кто из девочек сделал больше флажков, а кто – меньше? Кто работал больше времени, а кто – меньше? Кто работал быстрее, а кто – медленнее? Какие величины характеризуют работу? Как они связаны между собой?
1) 40:2=20 (ф.) — в час делает Валя.
2) 45:3=15 (ф.) — в час делает Галя.
20>15
Ответ: Валя сделала больше. Галя работала дольше. Валя работает быстрее Гали.
Работу характеризует производительность, количество сделанных штук в час.
Ответы к странице 46
2. Объясни смысл предложений:
а) Оля лепит пельмени с производительностью 2 штуки в минуту. 2 пельменя в минуту может слепить Оля.
б) Денис делает табуретки с производительностью 4 табуретки в день. Денис может сделать 4 табуретки за час.
в) Гена копает картошку с производительностью 3 ведра в час. Гена выкапывает 3 ведра картофеля за час.
г) Ира печатает текст с производительностью 120 знаков в минуту. 120 знаков за минуту набирает Ира.
Как из формулы работы найти производительность?
Как найти время работы?
w = A : t Производительность равна работе, делённой на время работы.
t = A : w Время равно работе, делённой на производительность.
3. Найди неизвестные значения величин по формуле работы А = w * t
| A | w | t |
| 60 шт. | 4 шт. /ч | 15 ч |
| 160 л | 8 л/мин | 20 мин |
| 450 шт. | 30 шт./с | 15 с |
| A | w | t |
| 240 зн. | 30 зн./мин | 8 мин. |
| 48 шт. | 12 шт./с | 4 с |
| 480 т | 80 т/ч | 6 ч |
4. а) Завод выпускает 208 автомобилей в день. Сколько автомобилей выпустит завод в год? (Считать, что в году 256 рабочих дней.)
208 * 256 = 53 248 (авт.) — выпустит завод за год.
х208
256
+1248
1040
416
53248
Ответ: 53 248 автомобилей.
б) Автомат закрыл 10 800 банок за 6 ч. С какой производительностью он работает?
10 800 : 6 = 1800 (б./ч) — производительность автомата.
-10800| 6
6 |1800
— 48
48
0
Ответ: 1800 банок в час.
5. Мастер вытачивает 8 деталей в час. Сколько деталей он сделает за 2 ч, 4 ч, 6 ч, 7 ч, 9 ч, t ч? Заполни в тетради таблицу. Запиши формулу зависимости работы A, выполненной мастером, от времени работы t
| t час | 2 | 4 | 6 | 7 | 9 | t |
| А дет | 16 | 32 | 48 | 56 | 72 | A = 8 * t |
ГДЗ к странице 47
6. Тане надо вымыть 36 тарелок. Сколько времени она затратит на эту работу, если будет мыть в минуту 2 тарелки, 3 тарелки, 4 тарелки, 6 тарелок, 9 тарелок, w тарелок? Заполни таблицу. Запиши формулу зависимости времени работы t от производительности w.
| w тар./мин | 2 | 3 | 4 | 6 | 9 | w |
| t мин. | 18 | 12 | 9 | 6 | 4 | t = 36 : w |
7. Выполни действия:
а) 152 • 387 = 58 824
б) 492 • 604 = 297 168
в) 999 • 555 = 554 445
г) 333 • 707 = 235 431
8. Вычисли. Расположи ответы примеров в порядке убывания и расшифруй название цветка. Узнай, почему он так называется.
НИМФЕЯ
* Свое латинское название – нимфея, по легенде цветок получил в честь греческой нимфы, навеки погрузившейся в подводные пучины из-за неразделенной любви.
9. Составь программу действий и вычисли:
2 3 5 1 4
а) 234 240 : 6 • 9 – (20 030 – 7358) : 4 = 348 192
5 2 6 1 3 4
б) 834 024 + 7900 • 25 – (483 • 504) : 8 • 10 = 727 234
1)
х483
504
+1932
2415
243432
2)
х7900
25
+ 395
158
197500
3)
— 243432| 8
24 |30429
-34
32
-23
16
— 72
72
0
4) 30429 * 10 = 304 290
5)
+834024
197500
1031524
6)
-1031524
304290
727234
7 дм 5 мм > 75 мм
9 м 2 дм < 920 дм
2 км 32 м = 203 200 см
6 т 8 ц = 6 800 кг
6 кг 8 г < 6 800 г
6 ч 8 мин > 68 мин
11. Реши уравнения с комментированием и сделай проверку:
а) (700 : x + 20) : 4 = 40;
700 : x + 20 = 40 * 4 ;
700 : x = 160 — 20;
х = 700 : 140;
х = 5.
Проверка:
(700 : 5 + 20) : 4 = 40;
40 = 40.
Ответ: х = 5.
б) 2 • (500 – y : 3) = 820;
500 – y : 3 = 820 : 2;
500 – y : 3 = 410;
y : 3 = 500 — 410;
y : 3 = 90;
у = 90 * 3;
у = 270.
Проверка:
2 • (500 – 270 : 3) = 820;
820 = 820.
Ответ: у = 270.
12. Запиши множество делителей и множество кратных числа 27.
13. Проведи прямую а. Отметь на рисунке точки K, L, M и N, такие что K ∈ a, L ∉ a, M ∉ a, N ∈ a.
14. Пусть A – множество чисел, меньших 5, а B – множество чисел, больших, чем 2, но меньших 7. Запиши множества A и B с помощью фигурных скобок. Найди их объединение и пересечение. Нарисуй диаграмму Эйлера–Венна.
Ответы к странице 48
1. Прочитай задачу и объясни, как составлена таблица. Составь план решения задачи и найди ответ. «Один оператор набрал на компьютере за 5 часов 90 страниц рукописи, а другой за 7 часов – 98 страниц. У кого из них производительность больше и на сколько?»
| A | w | t | |
| I | 90 стр. | на ? стр. | 5 ч |
| II | 98 стр. | 7 ч |
Найдем производительность первого оператора, вычислив, сколько страниц рукописи он набирает на компьютере за 1 час, если за 5 часов он набрал 90 страниц. Найдем производительность второго оператора, вычислив, сколько страниц рукописи он набирает на компьютере за час, если известно, что за 7 часов он набрал 98 страниц. Найдем, на сколько производительность первого оператора выше производительности второго.
1) 90 : 5 = 18 (стр./час) — производительность первого оператора.
2) 98 : 7 = 14 (стр./час) — производительность второго оператора.
3) 18 — 14 = 4 (стр./час) — разница производительности первого и второго оператора.
Ответ: производительность первого оператора выше производительности второго оператора на 4 стр./час.
2. Реши задачи с помощью таблиц:
а) За 6 дней на фабрике сшили 1926 костюмов. Сколько костюмов сошьют на этой фабрике за год (256 рабочих дней), если будут работать с той же производительностью?
| A | w | t | |
| I | 1926 к. | одинаковая ? к./дн. | 6 д. |
| II | ? к. | 256 д. |
Так как 1926 костюмов сшито за 6 дней, выясним сколько костюмов будет пошито за один день. Для этого общее количество костюмов делим на количество дней: Когда известно сколько шьют костюмов за один день, легко узнаем сколько их могут сшить за любой промежуток времени, в данной задаче за год (то есть 256 рабочих дней). Для этого умножим на 256 дней полученное 321 количество костюмов за один день.
1)1926 : 6 = 321 (к.) — шьют за день.
2) 321 * 256 = 82176 (к.) — сошьют за год.
Ответ: 82 176 костюмов будет пошито за год.
б) Экскаватор за 1 час копает 18 м канавы. Одну канаву он выкопал за 7 ч, а другую – за 19 ч. Сколько метров канавы выкопал экскаватор за всё это время?
| A | w | t | |
| I | м? | одинаковая 18 м/ч | 7 ч |
| II | м? | 19 ч |
Найдем сколько метров канавы выкопал экскаватор за 7 часов: Найдем сколько метров канавы выкопал экскаватор за 19 часов: Найдем сколько всего метров канавы выкопал экскаватор.
1) 18 * 7 = 126 (м) — одна канава.
2) 18 * 19 = 342 (м) — вторая канава.
3) 126 + 342 = 468 (м) — канавы выкопал экскаватор за это время.
Ответ: 468 метров канавы выкопал экскаватор за это время.
3. а) Два друга взяли в библиотеке одинаковые книги. Первый читает 3 страницы в день, а второй – 9 страниц в день. Кто из них прочитает эту книгу раньше и на сколько дней, если в книге 360 страниц?
Для решения задачи найдем за сколько дне прочитает книгу первый друг, если он в день будет читать 8 страниц. Во втором действии вычислим количество дней за которые прочитает книгу второй друг, читая в день по 9 страниц. Определим на сколько дней раньше второй друг прочитает книгу, чем прочитает первый друг.
1) 360 : 8=45 (дн.) — за столько дней прочитает книгу первый друг.
2) 360 : 9=40 (дн.) — за столько дней прочитает книгу второй друг.
3) 45-40=5 (дн.) — на столько дней быстрее прочитает книгу второй друг, чем второй.
Ответ: 5 дней.
б) Мастер сделал на станке 72 детали за 3 часа. Сколько деталей он сделает за 8 часов, если будет работать с той же производительностью?
Вычислим производительность мастера, с которой он должен работать, то есть найдем количество деталей, изготавливаемых им за 1 час. Зная производительность (24 дет./ч.) и время (8 ч.), можно вычислить количество деталей, которое изготовит мастер за это время.
1) 72 : 3 = 24 (дет./ч.) — производительность
2) 24 * 8 = 192 (дет.) — сделает мастер
Ответ: 192 детали.
4. Маляр должен покрасить заводской забор длиной 243 м. Первые 3 дня он красил по 18 м забора в день. За сколько времени он выполнил всю работу, если в оставшиеся дни он увеличил производительность на 3 метра в день?
Определим, какую длину забора покрасил маляр за первые три дня работы. Определим производительность маляра в последующие дни. Определим, какую длину забора покрасил маляр в последующие дни. Определим, за какое количество дней маляр покрасил 189 метров забора. Определим, за какой промежуток времени был покрашен весь забор.
1) 3 * 18 = 54 (м) — покрасил за 3 дня.
2) 3 + 18 = 21 (м/день) производительность после 3 дня.
3) 243 – 54 = 189 (м) — осталось покрасить после 3 дней.
4) 189 : 21 = 9 (д.) — будет красить еще после 3 дней
5) 9 + 3 = 12 (д.) — красил всего.
Ответ: вся работа была выполнена за 12 дней.
Ответы к странице 49
5. Найди ошибки в записи и решении примеров: Запиши и реши их в тетради правильно.
х309
709
+ 2781
2163
219081
6. Выполни действия. Проверь результаты с помощью калькулятора.
а) 254 • 966 = 245 364
б) 809 • 421 = 340 589
в) 358 • 604 = 216 232
г) 705 • 108 = 76 140
7. а) По формуле a = b • c + r, r < b найди делимое, если делитель равен 8, частное 25, а остаток 5.
б) Выполни деление с остатком и сделай проверку:
Проверка: 139475 * 7 + 1 = 976326
702 514 : 5 = 140 520 (остаток. 4
-702514| 5
5 |140520
— 20
20
— 25
25
— 14
10
4 (остаток)
Проверка: 140520 * 5 + 4 = 702 514
183 600 : 70 = 183 600
-183600 |70
14 |2622
-43
42
-16
14
-20
14
60 (остаток)
Проверка: 26220 * 70 + 60 = 183600
8. Найди значение выражения:
1 4 5 3 2
(720 – 99) • 324 – (728 + 50 • 90) = 195 976
1) 720 — 99 = 621
2) 50 * 90 = 4500
3) 728 + 4500 = 5228
4)
х621
324
+2484
1242
1863
201204
9. Реши уравнения с комментированием:
а)
(720 – t • 6) : 9 = 60
720 – t • 6 = 60 * 9 — переносим делитель в другую часть равенства, раскрываем скобки
t • 6 = 720 — 540 — переносим t*6 в другую часть, собираем все числа с одной стороны.
t • 6 = 180 — вычисляем числа
t = 30
б)
4 • (250 : a + 12) = 68
250 : a + 12 = 68 : 4 — переносим множитель, раскрываем скобки
250 : a = 17 — 12 — переносим числа в одну сторону
250 : a = 5 — вычисляем
а = 250 : 5
а = 50
10. Вычисли. Расположи ответы в порядке убывания. Расшифруй, как называли в Древнем Риме богинь красоты? Узнай, сколько их было? Какие у них имена?
Г
90 • 3 + 20 – 140 : 5 = 270 + 20 — 28 = 262
Р
130 • 2 – 360 : 30 = 260 — 120 = 140
А
(400 – 25 • 3 • 2) : 10 = (400 — 150) : 10 = 250 : 10 = 25
Ц
(270 – 240 : 4 • 3) : 9 = (270 — 60 * 3) : 9 = 90 : 9 = 10
И
(17 + 7 • 9 + 5 • 8) : 20 = (17 + 63 + 40) : 20 = 120 : 20 = 6
Я
140 + 60 – 280 : 7 • 5 = 200 — 40 * 5 = 0
ГРАЦИЯ
* В средневековом искусстве, три грации — это Добродетель, Красота и Любовь
11. Запиши множество делителей и множество кратных числа 28.
12. Ребро куба равно 11 см. Найди площадь поверхности куба и сумму длин всех его рёбер. Чему равен объём этого куба?
1) 11 * 11 = 121 (см 2 ) — площадь грани.
2) 121 * 6 = 726 (см 2 ) — площадь поверхности куба.
3) 11 * 11 * 11 = 1331 (см 3 ) — объем куба.
Ответ: 1331 см 3 объем куба.
13. Какое число следует за самым большим 20-значным числом?
10 000 000 000 000 000 000
14. Сколько квадратов ты видишь на рисунке?
14 маленьких + 6 состоящих из 4 квадратов, то есть 14 + 6 = 20 квадратов.
Ответы к странице 50
1. Выбери примеры на умножение круглых чисел и вычисли:
а) 725 • 8200 = 5 945 000
б) 349 • 506 = 176594
в) 8070 • 3680 = 807 * 368 * 100 = 296976 *100 = 29 697 600
г) 40 300 • 9040 = 4030 * 904 * 100 = 3 643 120 * 100 = 364 312 000
2. Найди производительность, если:
а) бабушка связала 36 рядов за 3 часа;
б) ученик прочитал 270 слов за 6 минут;
в) садовник посадил 54 цветка за 2 часа;
г) завод выпустил 480 машин за 4 дня
3. Найди пропущенные значения величин:
| A | w | t |
| 72 шт. | 12 шт./ч | 6 ч. |
| 150 т. | 50 т/мин | 3 мин |
| 400 домов | 80 д./год | 5 лет |
| A | w | t |
| 56 шт. | 8 шт./с | 7 с |
| 900 м | 150 м/день | 6 дней |
| 420 шт. | 30 шт./ч | 14 ч. |
4. Мастер получил заказ на изготовление 600 деталей. Первые 4 часа он делал по 70 деталей в час. Затем он увеличил производительность на 10 деталей в час. За сколько часов он выполнил весь заказ?
| A | w | t | |
| Вначале | ? ? >600 д. | 70 д./ч | 4ч 7ч >? |
| Потом | (70 + 10) д./ч |
1) 4 * 70 = 280 (дет.) — сделал за первые 4 часа.
2) 70 + 10 = 80 (дет./ч) стала производительность.
3) 600 — 280 = 320 (дет.) осталось сделать после 4 часов.
4) 320 : 80 = 4 (ч.) понадобилось, чтобы сделать 320 дет с производительностью 80 дет./ час.
5) 4 + 4 = 8 (ч.) за это время токарь выполнил заказ.
Ответ: 8 часов.
5. Реши задачи и сравни их. Что ты замечаешь?
а) Токарь вытачивает 240 деталей за 3 дня, а его ученик – за 4 дня. На сколько производительность токаря выше производительности ученика? Придумай свою задачу.
1) 240 : 3 = 80 (дет./день) — производительность токаря.
2) 240 : 4 = 60 (дет./день) — производительность ученика.
3) 80 — 60 = 20 (дет/день) — на столько производительность токаря выше, чем его ученика.
Ответ: на 20 дет/день.
б) У Димы в копилке 240 р. Он может купить на них 3 книги по одной цене или 4 одинаковых альбома. На сколько альбом дешевле книги?
1) 240 : 3 = 80 (р.) — стоит книга.
2) 240 : 4 = 60 (р.) — стоит альбом.
3) 80 — 60 = 20 (р.) — на столько альбом дешевле книги.
Ответ: на 20 р.
в) Расстояние между Москвой и Ярославлем равно 240 км. Автобус проходит это расстояние за 4 ч, а поезд – за 3 ч. На сколько километров в час скорость поезда больше скорости автобуса?
1) 240 : 3 = 80 (км/ч) — скорость поезда.
2) 240 : 4 = 60 (км/ч) — скорость автобуса.
3) 80 — 60 = 20 (км/ч) — на столько скорость поезда больше скорости автобуса.
Ответ: на 20 км/ч.
г) Бассейн, объём которого 240 м3, наполняется первой трубой за 3 ч, а второй трубой – за 4 ч. На сколько скорость наполнения бассейна первой трубой больше скорости наполнения второй трубой? Придумай задачу с другими величинами, которая решается так же.
1) 240 : 3 = 80 (м 3 /час) — расход первой трубы.
2) 240 : 4 = 60 (м 3 /час) — расход второй трубы.
3) 80 — 60 = 20 (м 3 /час) — на столько производительность (расход) из первой трубы, больше чем со второй.
Ответ: на 20 м 3 /час.
Все задачи решаются с одинаковыми операциями по вычислению, но разными по смысловой нагрузке.
Папа за 3 часа собрала на сборке картофеля выкопал которого 240 штук, а сын такое же количество за 4 часа. На сколько производительность отца выше, чем сына?
Ответы к странице 51
6. Вычисли. Расположи ответы примеров в порядке убывания. Кто это? Найди информацию о нём в Интернете или энциклопедии.
7. Вычисли и сравни значения выражений. Что ты замечаешь?
3 1 2
3 524 120 – 398 705 : 5 • 40 = 334 480
1)
-398705| 5
35 |79741
— 48
45
-37
35
— 20
20
— 5
5
0
2)
х79741
40
+3189640
3)
-3524120
3189640
334480
1 2 3
(3 524 120 – 398 705) : 5 • 40 = 25 003 320
1)
3524120
– 398705
3125415
2)
— 3125415| 5
30 |625083
— 12
10
— 25
25
— 41
40
-15
15
0
3)
х625083
40
25003320
2 1 3
(3 524 120 – 398 705 : 5) • 40 = 137 775 160
1)
— 398705 |5
35 |79741
-48
45
-37
35
— 20
20
— 5
5
0
2)
— 3524120
79741
3444379
3)
х3444379
40
137775160
8. Выполни действия:
а) 7 м 85 см • 412 = 323 420 см = 3234 м 20 см = 3 км 234 м 20 см
х785
412
+1570
785
3140
323420
б) 4 см 2 6 мм 2 • 503 = 204 218 мм 2 = 2042 см 2 18 мм 2
х406
503
+ 1218
2030
204218
в) 6 дм 3 94 см 3 • 904 = 988 976
х1094
904
+ 4376
9846
988976
г) 3 кг 68 г • 706 = 2 166 008
х3068
706
+ 18408
21476
2166008
д) 8 мин 24 с • 375 = 189 000 с = 3150 мин
8 мин = 60 * 8 = 480 с
х504
375
+ 2520
3528
1512
189000
е) 1 ч 15 мин • 576 = 43200 мин = 720 ч
9. Площадь нижней грани прямоугольного параллелепипеда равна 800 см2. Определи высоту этого параллелепипеда, если его объём равен 24 000 см
1) 24 000 : 800 = 30 (см) высота параллелепипеда.
Ответ: 30 см.
10. Напиши формулу объёма прямоугольного параллелепипеда, если у него:
а) длина равна 8, ширина 4, высота c; 8 * 4 * с = 32 * с
б) площадь основания 45, а высота h; 45 * h
в) площадь основания S, а высота h; S * h
11. Рассмотри таблицы. Как связаны между собой переменные x и у ? Составь формулу, выражающую y через x.
12. На рисунке все фигуры, кроме одной, имеют общее свойство. Какая фигура «лишняя»?
* лишний треугольник, так как пересекаемые отрезки пересекаются не в центре, то есть он не удовлетворят условию центральной симметрии.
Ответы к странице 52
1. Проанализируй, как связаны между собой величины каждой строки. Запиши формулу зависимости между ними. Что общего у всех записанных формул? Замени все формулы одной общей формулой.
1 — S = v * t
2 — C = a * n
3 — A = w * t
4 — S = a * b
5 — V = a * t
6 — K = k * n
7 — T = t * n
8 — М = м * n
9 — P = p * n
Формула произведения
Формулы зависимостей между величинами – такие, как формула пути (s = v • t), формула стоимости (C = a • n), формула работы (A = w • t) и др., – можно записать одной общей формулой: a = b • cЭту общую формулу мы будем называть формулой произведения.
Величины b и c в формуле произведения можно найти по общему правилу нахождения неизвестного множителя:
b = a : c c = a : b
Страница 53
2. Реши задачи. Сравни их условия и решения.
а) Турист прошёл в первый день 32 км, а во второй – 24 км. Всего он шёл в эти 2 дня 14 часов. Сколько времени шёл турист в каждый из этих дней, если его скорость не изменялась?
1) 32 + 24 = 56 (км) — прошел турист за 2 дня.
2) 56 : 14 = 4 (км/ч) — была скорость туриста.
3) 32 : 4 = 8 (ч.) — прошел в первый день.
4) 24 : 4 = 6 (ч.) — прошел во второй день.
Ответ: 8 часов в первый день и 6 часов во второй.
б) Первый мастер сделал 32 игрушки, а второй – 24 игрушки. На всю эту работу в сумме они затратили 14 часов. Сколько времени работал каждый мастер, если их производительность одинаковая?
1) 32 + 24 = 56 (игр.) — сделали 2 мастера.
2) 56 : 14 = 4 (игр./ч) — производительность.
3) 32 : 4 = 8 (игр.) — сделал первый мастер.
4) 24 : 4 = 6 (игр.) — сделал второй мастер.
Ответ: 8 игрушек сделал первый мастер и 6 игрушек второй.
в) Две подружки из Цветограда купили вместе 14 одинаковых воздушных шариков. Первая уплатила за свою покупку 32 монеты, а вторая – 24 монеты. Всего они купили 14 шариков. Сколько шариков купила каждая из подруг?
1) 32 + 24 = 56 (м.) — потратили.
2) 56 : 14 = 4 (м.) — стоимость шарика.
3) 32 : 4 = 8 (ш.) — купила первая подруга.
4) 24 : 4 = 6 (ш.) — купила вторая подруга.
Ответ: 8 шар первая и 6 шариков вторая.
г) Из двух отрезов шёлка сшили 14 одинаковых юбок. В первом отрезе было 32 м, а во втором – 24 м. Сколько юбок сшили из каждого отреза?
1) 32 + 24 = 56 (м) — ткани было всего.
2) 56 : 14 = 4 (м) — надо на юбку.
3) 32 : 4 = 8 (юб.) — сшили с первого отрезка.
4) 24 : 4 = 6 (юб.) — сшили со второго отрезка.
Ответ: 8 юбок с первого и 6 со второго.
Что ты замечаешь? Как это можно объяснить?
Задачи с одними и теми же операциями по порядку и по номиналу используемых величин, так как исходные номинальные данные тоже одинаковые, а алгоритмы решения схожи.
Ответы к странице 54
3. Реши задачи. Для каждой из них придумай задачу с другими величинами, которая решается так же.
а) Алёша купил 3 календарика по 8 р. и 7 открыток по 12 р. за штуку. Сколько всего денег заплатил Алёша?
3 * 8 + 7 * 12 = 24 + 84 = 108 (р.) — всего заплатил.
Ответ: 108 рублей.
б) Фрегат проплыл сначала 2 ч, а потом ещё 4 ч с той же скоростью. Всего он проплыл 216 км. С какой скоростью он плыл?
1) 2 + 4 = 6 (ч) — всего плыл фрегат.
2) 216 : 6 = 36 (км/ч) — скорость фрегата.
Ответ: 36 км/ч.
в) Дима почистил 12 картофелин за 6 мин, а Ира – 15 картофелин за 5 мин. Кто из них чистит картошку быстрее и на сколько?
1) 12 : 6 = 2 (к./мин) — производительность Димы.
2) 15 : 5 = 3 (к./мин) — производительность Иры.
3) 3 — 2 = 1 (к./мин) — на столько быстрее чистит Ира.
Ответ: быстрее чистит Ира на 1 картошку в минуту.
4. Составь программу действий и вычисли:
1 2 4 3 7 5 6
а) (154 800 : 10 : 9 – 47 • 6) • (97 840 : 80 + 77) = 1 869 400
1) 154 800 : 10 = 15 480
2)
-15480| 9
9 |1720
-64
63
-18
18
0
3) 47 * 6 = 240 + 42 = 282
4) 1720 — 282 = 1438
5) 97840 : 80 = 9784 : 8 = 1223
— 9784 |8
8 |1223
-17
16
— 18
16
— 24
24
0
6) 1223 + 77 = 1300
7)
х1438
1300
+4314
1438
1869400
2 3 7 4 1 5 8 6
б) 76 000 • 90 : 1000 – 96 : (48 : 8) • 109 – 5400 : 600 = 5087
1) 48 : 8 = 6
2) 76 000 • 90 = 76 * 9 * 10 000 = (630 + 54) * 10 000 = 6 840 000
3) 6 840 000 : 1000 = 6 840
4) 96 : 6 = 16
5)
х16
109
+ 144
16
1744
6) 5400 : 600 = 9
7) 6 840 — 1744 = 5096
8) 5096 — 9 = 5087
5. Запиши множества делителей чисел 7 и 31. Что общего у этих двух множеств? Придумай своё число, множество делителей которого обладает тем же свойством.
Для 7 это 1, 7, то есть число простое.
Для 31 это 1, 31 то есть число тоже простое.
Любое простое число обладает теми же свойствами, делится на 1 и на само себя. Скажем 2 или 3. Подробнее в статье «Простые числа».
6. Реши уравнения с комментированием и сделай проверку:
а) делим. делит. разн.
(3 • m – 20) : 5 = 50;
3 • m – 20 = 50 * 5;
ум. выч. разн
3 • m – 20 = 250;
3 • m = 250 + 20;
мн. мн. пр.
3 • m = 270;
m = 270 : 3;
m = 9.
Проверка:
(3 • 9 – 20) : 5 = 50;
50 = 50.
Ответ: m = 9.
б) слаг. слаг. сум.
480 : (13 – t) + 20 = 100;
480 : (13 – t) = 100 — 20;
делим. делит. разн
480 : (13 – t) = 80;
13 – t = 480 : 80;
ум.выч.разн
13 – t = 6;
t = 13 — 6;
t = 7.
Проверка:
480 : (13 – 7) + 20 = 100;
100 = 100.
Ответ: t = 7.
7. Выполни действия. Расположи ответы примеров в порядке убывания и расшифруй название игры. Узнай, как играют в эту игру.
х4750
750
+23750
33250
35625400
У 417 * 2450 = 1 021 650
Р 862 * 980 = 844 760
И 932 * 708 = 659 856
М 806 * 547 = 440 882
Е 539 * 694 = 374 066
* Буриме (фр. bouts-rimés «рифмованные концы») — литературная игра, заключающаяся в сочинении стихов, чаще шуточных, на заданные рифмы.
8. Запиши множество трёхзначных чисел, которые:
не изменяются при чтении их слева направо и справа налево;
при этом их сумма цифр равна
Трехзначные числа, которые одинаково читаются слева направо и справа налево имеют вид: 1*1, 2*2, 3*3, 4*4. Затем находим среднюю цифру, вычитая из 9 сумму двух известных цифр.
Ответ: 171, 252, 333, 414.
9. У пятерых крестьян – Ивана, Петра, Якова, Михаила и Герасима – было вместе 11 овец. Не могли они найти пастуха. И говорит Иван: «Будем, братцы, пасти овец по очереди – по столько дней, сколько каждый из нас имеет овец». У Ивана в 2 раза меньше овец, чем у Петра. У Якова – в 2 раза меньше, чем у Ивана. Михаил имеет овец в 2 раза больше, чем Яков, а Герасим – в 2 раза меньше, чем Пётр. По сколько дней должен каждый из них пасти овец?
Составляем уравнение. Берем за х овец у Герасима, как у того у кого меньше всего овец.
2х + 4х + х + 2х + х=10
10 * x = 10
х=1
Тогда логически получаем.
Иван — 1 * 2 = 2 овцы, т.е. 2 дня
Петр — 1 * 4 = 4 овцы, т.е. 4 дня
Яков — 1 овца, т.е. 1 день
Михаил — 1 * 2 = 2 овцы, т.е. 2 дня
Герасим — 1 овца, т.е. 1 день
Ответы к странице 55
1. Реши уравнения и сделай проверку:
а) 3600 : (18 – x) – 120 = 280;
3600 : (18 – x) = 280 + 120;
3600 : (18 – x) = 400;
18 – x = 3600 : 400;
18 – x = 9;
х = 18 — 9;
х = 9.
Проверка:
3600 : (18 – 9) – 120 = 280;
280 = 280.
Ответ: х = 9.
б) (y : 8 + 18) • 9 = 540;
y : 8 + 18 = 540 : 9;
y : 8 + 18 = 60;
y : 8 = 60 — 18;
y : 8 = 42;
y = 42 *8;
у = 336.
Проверка:
(336 : 8 + 18) • 9 = 540;
540 = 540.
Ответ: у = 336.
а) Строитель уложил m кирпичей за 4 ч. За сколько времени он уложит d кирпичей, если будет работать с той же производительностью?
б) Самолёт пролетел s км за 2 ч, а вертолёт пролетел это же расстояние за 3 ч. На сколько скорость самолёта больше скорости вертолёта?
в) За 6 м льняной ткани заплатили k р. А один метр шёлка на n р. дороже метра льняной ткани. Чему равна цена метра шёлка?
г) Мастеру надо было изготовить a деталей. Он уже сделал b деталей. Чему должна быть равна его производительность, чтобы он успел сделать оставшиеся детали за t часов? Для одной из данных задач придумай задачу с другими величинами, которые решаются так же
* своя задача как вариант в
За 8 пачек сушек заплатили 160 р. А одно мороженое на 10 р. дороже пачки сушек. Чему равна цена мороженого?
160 : 8 + 10 = 30 (р.)
3. Вырази в указанных единицах измерения:
а)
5 дм 6 мм = 506 мм
5 м 6 см = 5060 мм
5 км 6 м = 5006 м
5 км 6 м = 50060 дм
5 км 6 м = 5006000 мм
б)
5 ц 6 кг = 506 кг
5 кг 6 г = 5006 г
5 сут. 6 ч = 126 ч
5 мин 6 с = 306 с
5 ч 6 мин = 306 мин
4. Выполни действия:
а) 3 т 2 ц 6 кг – 29 ц 48 кг = 3206 кг — 2948 кг = 258 кг
в) 9 мин 15 с · 8 = 9 * 8 мин + 15 * 8 с = 72 мин + 120 с = 74 мин
б) 5 км 19 м + 1 км 981 м = 5019 м + 1981 м = 7000 м = 7 км
г) 6 м 1 дм 2 мм : 3 = 6102 мм : 3 = 2034 мм = 2 м 3 см 4 мм
5. Для сада купили в питомнике 14 кустов красной и чёрной смородины по одинаковой цене. За красную смородину заплатили 250 р., а за чёрную – 450 р. Каких кустов купили больше и на сколько?
1) 250 + 450 = 700 (р.) — заплатили за все кусты.
2) 700 : 14 = 50 (р.) — стоит куст смородины.
3) 450 — 250 = 200 (р.) — на столько больше заплатили за черную смородину.
4) 200 : 50 = 4 (к.) — на столько больше кустов купили черной смородины.
Ответ: на 4 куста больше купили черной смородины.
Ответы к странице 56
6. В пошивочной мастерской в первый день сшили 24 одинаковых комплекта белья, а во второй – на два таких комплекта больше. На все комплекты было израсходовано за два дня 800 м ткани. Сколько метров ткани израсходовали в каждый из этих дней?
1) 24 + 2 = 26 (к.) — сшили во второй день.
2) 24 + 26 = 50 (к.) — сшили за 2 дня.
3) 800 : 50 = 13 (м) — надо для пошива комплекта белья.
4) 24 * 13 = 312 (м) — ткани потратили на 24 комплекта в 1 день.
5) 26 * 13 = 338 (м) — ткани потратили на 26 комплекта во 2 день.
Ответ: 312 и 338 метров ткани.
7. Найди значения выражений:
5 6 8 7 1 9 2 3 4
а) 270 : 9 • 7 – 360 : (16 : 4) + (42 : 7 • 6 + 14) = 170
1) 16 : 4 = 4
2) 42 : 7 = 6
3) 6 * 6 = 36
4) 36 + 14 = 50
5) 270 : 9 = 30
6) 30 * 7 = 210
7) 360 : 4 = 90
8) 210 — 90 = 120
9) 120 + 50 = 170
7 8 1 10 2 3 4 9 5 6
б) 125 • 0 : (45 • 4) + (120 • 10 : 100 – 8) • (15 • 1000 : 5) = 12 000
1) 45 * 4 = 180
2) 120 * 10 = 1200
3) 1200 : 100 = 12
4) 12 — 8 = 4
5) 15 * 1000 = 15 000
6) 15 000 : 5 = 3000
7) 125 * 0 = 0
8) 0 : 180 = 0
9) 4 * 3000 = 12000
10) 0 + 12 000 = 12 000
8. Выполни умножение. Найди сумму и разность самого большого и самого маленького из получившихся чисел:
2590 • 763 = 1 976 170
9450 • 4560 = 43 092 000
49 300 • 807 = 39 785 100
43 092 000 − 1 976 170 = 41 115 830
9. Пересекаются ли:
а) прямая l и луч AB; ДА
б) прямая l и луч TS; НЕТ
в) прямая l и отрезок MK; НЕТ
г) прямая l и отрезок CD; ДА
д) лучи AB и TS; ДА
е) отрезки MK и CD; НЕТ
ж) луч TS и отрезок MK; НЕТ
з) луч TS и отрезок EF? НЕТ
10. Математическое исследование
а) Запиши число 16 всеми способами в виде произведения двух множителей. Для каждого способа найди сумму множителей. В каком случае получилась наименьшая сумма?
б) Проделай то же самое с числом 36, затем с числом 64. Какое можно высказать предположение (гипотезу)?
16 = 1 * 16; 1 + 16 = 17.
16 = 2 * 8; 2 + 8 = 10.
16 = 4 * 4; 4 + 4 = 8.
16 = 8 * 2; 8 + 2 = 10.
16 = 16 * 1; 16 + 1 = 17.
Наименьшая сумма получилась при сложении равных множителей.
36 = 1 * 36; 1 + 36 = 37.
36 = 2 * 18; 2 + 18 = 20.
36 = 3 * 12; 3 + 12 = 15.
36 = 4 * 9; 4 + 9 = 13.
36 = 6 * 6; 6 + 6 = 12.
36 = 9 * 4; 9 + 4 = 13.
36 = 12 * 3; 3 + 12 = 15.
36 = 18 * 2; 18 + 2 = 20.
36 = 36 * 1; 36 + 1 = 37.
Наименьшая сумма получилась при сложении равных множителей.
64 = 1 * 64; 1 + 64 = 65.
64 = 2 * 32; 2 + 32 = 34.
64 = 4 * 16; 4 + 16 = 20.
64 = 8 * 8; 8 + 8 = 16.
64 = 16 * 4; 16 + 4 = 20.
64 = 32 * 2; 32 + 2 = 34.
64 = 64 * 1; 64 + 1 = 65.
Наименьшая сумма получилась при сложении равных множителей. Можно утверждать, что данная гипотеза верна для всех чисел, которые представляются в виде произведения двух равных множителей.
11. У Романа есть красные и зелёные кубики. Сторона зелёного кубика в два раза больше стороны красного. Роман построил большой куб из 64 красных кубиков. Сколько нужно зелёных кубиков, чтобы построить точно такой же куб?
Получается так, что в объеме зеленого кубика помещается 4 красных кубиков. Тогда
64 * 4 = 256 (к.) — красных, надо взять, чтобы построить такой же куб как из 64 зеленых.
Ответ: 256 кубиков.
Ответы к странице 57
12. Вычисли. Расшифруй и отгадай загадку.
П 12 — 4 + 7 = 15
О 9 + 3 — 6 = 6
Ч 30 — 4 — 0 = 26
Т 51 — 7 + 5 = 49
И 82 — 42 + 3 = 43
Г 56 — 50 + 8 = 14
А 300 + 6 = 306
К 300 + 60 = 360
Ъ 300 + 600 = 900
Ц 830 — 30 = 800
Ы 830 — 800 = 30
Р 954 — 4 = 950
М 954 — 50 = 904
Е 954 — 900 = 54
Н 203 + 70 = 273
Ь 592 + 8 = 600
Й 358 + 6 = 404
Д 462 — 5 = 457
Ё 215 + 40 = 255
Ж 215 + 400 = 615
С 215 + 4 = 219
Л 300 — 7 = 293
В 498 + 8 = 506
Я 241 + 116 = 357
Б 678 — 235 = 443
Ш 529 + 12 = 541
У 453 — 16 = 437
ЧИСЛО Я — МЕНЬШЕ ДЕСЯТИ ТЕБЯ ЛЕГКО МЕНЯ НАЙТИ НО ЕСЛИ БУКВЕ Я ПРИКАЖЕШЬ РЯДОМ ВСТАТЬ Я ВСЕ ОТЕЦ И ТЫ И БАБУШКА И МАТЬ
Страница 58
С древнейших времён люди, умеющие решать арифметические задачи, пользовались большим уважением. Благодаря этому умению, можно было отвечать на многие жизненно важные практические вопросы. Не случайно в первом российском учебнике математики – «Арифметике» Л.Ф. Магницкого, изданной в 1703 году, – писалось: «Арифметика есть искусство честное, всем удобопонятное, много-полезнейшее и многохвалённейшее. ».
Овладеть искусством решения задач не просто. Во-первых, надо овладеть мастерством выполнения всех четырёх арифметических действий: сложения, вычитания, умножения и деления. Но и это ещё не всё. Главная трудность заключается в том, чтобы отыскать нужную последовательность арифметических операций, которая позволит найти неизвестную искомую величину.
Разнообразие задач иногда представляется бушующим океаном, в котором только случай может помочь беззащитному судну найти верный курс. Между тем имеются надёжные инструменты решения задач, которые помогут преодолеть любые препятствия всем, кто научится ими пользоваться.
Например, во всех простых задачах всё разнообразие взаимосвязей между величинами описывается всего лишь двумя общими форму-лами:a = b + c и a = b • cПоэтому алгоритм решения простых задач каждого из этих типов включает в себя 3 шага:
1) установить вид зависимости: a = b + c или a = b • c;
2) определить, какая из величин неизвестна (слагаемое, сумма, множитель, произведение);
3) выбрать соответствующее действие.
Разобраться в этих вопросах помогут в случае необходимости хорошо известные инструменты: схема (a = b + c) и таблица (a = b • c).
Ответы к странице 59
1. Определи тип простой задачи и реши её:
а) Миша нашёл 24 гриба, а Витя – в 3 раза меньше. Сколько грибов нашёл Витя?
24 : 3 = 8 (г.) — нашел Витя.
Ответ: 8 грибов.
б) Таня испекла 15 пирожков. Из них 8 пирожков съели за ужином. Сколько пирожков осталось?
в) Дима прошёл за 20 минут 1 км 600 м. С какой скоростью он шёл?
1600 : 20 = 80 (м/мин) — скорость с которой шел Дима.
Ответ: 80 м/мин.
г) Лариса посадила в своём цветнике 36 тюльпанов и 42 нарцисса. Каких цветов она посадила больше и на сколько?
42 — 36 = 6 (ц.) — больше посадили нарциссов.
Ответ: на 6 больше нарциссов.
Ответы к странице 60
2. В магазин привезли 120 кг яблок, груш – в 2 раза меньше, чем яблок, а персиков – на 12 кг больше, чем груш. Сколько всего килограммов яблок, груш и персиков привезли в магазин?
1) 120 : 2 = 60 (кг) — груш привезли.
2) 60 + 12 = 72 (кг) — привезли персиков.
3) 120 + 60 + 72 = 252 (кг) — всего килограммов яблок, груш и персиков привезли в магазин.
Ответ: 252 кг.
3. На шоссе стоят четыре восьмиэтажных жилых дома. На каждом этаже каждого из этих домов по 9 квартир. Из всех квартир 128 однокомнатных, 96 двухкомнатных, а остальные – трёхкомнатные. Сколько всего трёхкомнатных квартир в этих домах?
1) 4 * 8 * 9 = 32 * 9 = 288 (кв.) — всего в домах.
2) 128 + 96 = 224 (кв.) — однокомнатных и двухкомнатных.
3) 288 — 224 = 64 (кв.) трехкомнатные.
Ответ: 64 трехкомнатные квартиры.
4. Расстояние между Москвой и Минском 720 км. Автомобиль ехал из Москвы в Минск со скоростью 80 км/ч, а на обратном пути – увеличил скорость на 10 км/ч. Сколько времени затратил автомобиль на весь путь из Москвы в Минск и обратно?
1) 720 : 80 = 9 (ч.) — ехал из Москвы в Минск.
2) 80 + 10 = 90 (км/ч) — скорость из Минска в Москву.
3) 720 : 90 = 8 (ч.) — ехал из Минска в Москву.
4) 8 + 9 = 17 (ч) — ехал всего.
Ответ: 17 часов.
5. В первом куске 12 м ткани, а во втором – 8 м такой же ткани. Первый кусок дороже второго на 320 р. Сколько рублей стоит каждый из этих кусков ткани?
1) 12 — 8 = 4 (м) — на столько больше в первом куске.
2) 320 : 4 = 80 (р.) — стоит метр ткани.
3) 12 * 80 = 960 (р.) — стоит первым кусок.
4) 8 * 80 = 640 (р.) — стоит второй кусок.
Ответ: 960 и 640 рублей.
6. Сумма площадей двух прямоугольников, имеющих одинаковую длину, равна 220 дм2. Ширина первого прямоугольника 4 дм, а ширина второго – на 3 дм больше, чем первого. Чему равна длина этих прямоугольников?
1) 4 + 3 = 7 (дм) — ширина второго прямоугольника.
2) 4 + 7 = 11 (дм) — ширина первого и второго прямоугольника.
3) 220 : 11 = 22 (дм) — длина прямоугольников.
Ответ: 22 дм.
7. Выполни действия:
а) 374 • 75 = 28 050
б) 908 • 132 = 119 856
в) 850 • 39 800 = 33 830 000
г) 4620 • 5040 = 23 284 800
д) 7 263 000 : 90 = 80 700
е) 24 040 000 : 800 = 3050
8. Составь программу действий и вычисли:
1 4 2 3
а) (18 560 – 17 915) • (4235 : 5 + 9535) = 6 696 390
1)
— 18560
17915
645
4)
х10382
645
+ 51910
41528
62292
6696390
2 1 4 5 3
б) (600 300 – 728 • 604) : 4 • (1700 • 390) = 26 617 461 000
1)
х728
604
+ 2912
4368
439712
2)
— 600300
439712
160588
3)
х1700
390
+153
51
663000
4)
— 160588| 4
16 |40147
-5
4
-18
16
-28
28
0
5)
+ 40147
663000
+120441
240882
240882
26617461000
9. Игра «Распутай клубок». Расшифруй записи и вычисли указанные произведения:
4 + 3 = 7
9 — 4 = 5
2 + 6 = 8
3500 * 660 = 2310000
5604 * 473 = 2650692
767 * 504 = 386568
Ответы к странице 61
1. Составь задачи по таблицам и реши их. Что ты замечаешь? Придумай и реши аналогичные задачи на движение и стоимость.
а) Первая бригада за 8 дней изготовила 96 деталей, а вторая при той же производительности изготовила 60 деталей. Сколько дней ушло на работу у второй бригады?
1) 96 : 8 = 12 (дет./д.) — производительность бригады.
2) 60 : 12 = 5 (дней) — ушло на работу у второй бригады.
Ответ: 5 дней.
б) Площадь прямоугольника 96 см2, а второго 60 см2. Длины прямоугольников одинаковые, а ширина у первого 8 см. Сколько сантиметров ширина второго прямоугольника?
1) 96 : 8 = 12 (см) — длина прямоугольников.
2) 60 : 12 = 5 (см) — ширина второго прямоугольника.
Ответ: 5 сантиметров.
Один велосипедист проехал 96 км за 8 часов, а второй 60 км с той же скоростью. Сколько понадобилось времени второму велосипедисту?
1) 96 : 8 = 12 (км/ч) — скорость велосипедистов.
2) 60 : 12 = 5 (ч) — понадобилось второму велосипедисту.
Ответ: 5 часов.
8 пирожков с капустой стоят 96 рублей. При этом по той же цене можно купить пирожки с яйцом. Сколько пирожков с яйцом можно купить на 60 рублей?
1) 96 : 8 = 12 (р.) — стоит пирожок.
2) 60 : 12 = 5 (п.) — с яйцом можно купить.
Ответ: 5 пирожков.
2. Портниха за 4 дня сшила на 42 комплекта белья меньше, чем за 7 дней. С какой производительностью она работала? Сколько комплектов белья сошьёт эта портниха за 20 дней, если будет работать с той же производительностью?
1) 7 — 4 = 3 (д.) — портниха шила 42 комплекта.
2) 42 : 3 = 14 (ком./д.) — производительность.
3) 20 * 14 = 280 (комп.) — сошьет за 20 дней.
Ответ: производительность 14 комп./ день, сошьет 280 комплектов за 20 дней.
3. Составь и реши уравнения:
а) Задумано число. К нему прибавили 19, сумму умножили на 5 и из полученного произведения вычли 16. Получилось 139. Какое число задумано?
Составим уравнение
(х+19) * 5 — 16 = 139;
(х + 19) * 5 = 16 + 139;
х + 19 = 155 : 5;
х + 19 = 31;
х = 31 — 19;
х = 12.
Ответ: х = 12.
б) Задумано число. Его вычли из 480, разность разделили на 6 и полученное частное увеличили на 89. В результате получилось 165. Какое число задумано?
(480-х) : 6 +89 = 165;
(480-х) : 6 = 165-89;
480 — х = 76 * 6;
480 — х = 456;
х = 480 — 456;
х = 24.
Ответ: х = 24.
4. Составь программу действий и вычисли:
5 1 9 6 7 10 2 3 4 8
а) 560 : (720 : 90) – 900 : 50 • 3 + (6 • 8 : 4 + 28) : 5 = 36
1) 720 : 90 = 8
2) 6 * 8 = 48
3) 48 : 4 = 12
4) 12 + 28 = 40
5) 560 : 8 = 70
6) 900 : 50 = 14
7) 14 * 3 = 42
8) 40 : 5 = 8
9) 70 — 42 = 28
10) 28 + 8 = 36
6 1 2 3 9 7 4 10 8 5
б) 7 • (45 : 9 • 6 – 23) + 84 : (320 : 80) – 13 • (51 : 17) = 31
1) 45 : 9 = 5
2) 5 * 6 = 30
3) 30 — 23 = 7
4) 320 : 80 = 4
5) 51 : 17 = 3
6) 7 * 7 = 49
7) 84 : 4 = 21
8) 13 * 3 = 39
9) 49 + 21 = 70
10) 70 — 39 = 31
5. Найди значения произведений:
а) 3015 • 24 = 72 360
б) 527 • 609 = 320 943
в) 81 030 • 2600 = 210 678 000
г) 12 800 • 3560 = 45 568 000
д) 8170 • 706 = 5 768 020
е) 9030 • 9040 = 81 631 200
Ответы к странице 62
6. Выполни действия:
а) 5 ч 18 мин + 4 ч 56 мин = 300 мин + 18 мин + 240 мин + 56 мин = 614 мин = 10 ч 14 мин
б) 7 мин 2 с – 1 мин 35 с = 420 с + 2 с — 60 с — 35 с = 327 с = 5 мин 27 с
в) 2 т 30 кг – 12 ц 80 кг = 2000 кг + 30 кг — 1200 кг — 80 кг = 2030 кг — 1280 кг = 750 кг
г) 1 кг 236 г + 6 кг 764 г = 1000 г + 236 г + 6000 г + 764 г = 8000 г = 8 кг
7. В автопробеге Париж – Дакар участвовало 420 машин. Экипаж каждой машины состоял из 3 человек. До финиша не дошли 248 машин. Сколько спортсменов прибыли к финишу?
1) 420 — 248 = 172 (м.) — пришло на финиш.
2) 172 * 3 = 516 (с.) — прибыли к финишу.
Ответ: 516 спортсменов.
8. Несколько мальчиков ловили рыбу. Всего они поймали 75 рыб. Сколько было мальчиков, если двое поймали по 10 рыб, а остальные – по 11?
1) 2 * 10 = 20 (р.) — поймали 2 мальчика.
2) 75 — 20 = 55 (р.) — поймали остальные мальчики.
3) 55 : 11 = 5 (м.) — ловили еще, кроме 2 мальчиков.
4) 2 + 5 = 7 (м.) — было всего.
Ответ: 7 мальчиков.
9. Реши задачи и сравни их решения. Что ты замечаешь?
1) Магазин продал за день 16 одинаковых банок вишнёвого варенья и 20 таких же банок малинового. Малинового варенья было продано на 8 кг больше, чем вишнёвого. Сколько килограммов варенья каждого сорта было продано за этот день?
1) 20 — 16 = 4 (б.) — больше было проданного малинового варенья.
2) 8 : 4 = 2 (кг) — варенья в каждой банке.
3) 16 * 2 = 32 (кг) — было продано вишневого варенья.
4) 20 * 2 = 40 (кг) — было продано малинового варенья.
Ответ: 32 кг вишневого и 40 кг малинового.
2) Магазин продал за день 32 кг вишнёвого варенья и 40 кг малинового. Всё варенье было разложено в одинаковые банки, причём банок с вишнёвым вареньем было на 4 меньше, чем с малиновым. Сколько банок варенья каждого сорта было продано?
1) 40 — 32 = 8 (кг) — варенья было в 4 банках.
2) 8 : 4 = 2 (кг) — в каждой банке.
3) 32 : 2 = 16 (б.) — было продано вишневого варенья.
4) 40 : 2 = 20 (б.) — было продано малинового варенья.
Ответ: 16 банок и 20 банок.
10. Сравни выражения*:
118 + n > n + 45
k : 4 > k : 6
а • b – c < b • а + c
29 – b < 40 – b
14 • d < 21 • d
m • (n + k) > m • n + k
x – 35 > x – 45
50 : m > 15 : m
4 • х + 8 • х = (х • 6) • 2
11. Мастер изобрел автомобиль, работающий на воде. Полного бака хватает на 5 ч езды. Автомобиль может доехать из города А в город В, не считая времени на заправку, за 20 ч. Чтобы заправить полный бак, требуется 2 ч. Мастер выехал из города А с полным баком. Через сколько времени он прибудет в город В, если дорога идёт вдоль реки?
1) 3 * 2 = 6 (ч.) потребуется на заправку.
2) 20 + 6 = 26 (ч.) потребуется, чтобы доехать из города А в город В.
Ответ: 26 часов.
12. Продолжи закономерность на 3 числа:
а) 0, 15, 30, 45, 60, 75, 90, 105
б) 1, 4, 9, 16, 25, 36, 49, 64
Ответы к странице 63
1. Умножение натуральных чисел на четырёхзначное, пятизначное, шестизначное и т. д. число выполняется аналогично тому, как выполняется умножение на трёхзначное число, например:
2. Выполни действия:
а) 7032 • 2102 = 14 781 264
б) 80 800 • 7777 = 628381600
в) 12 340 • 5609 = 69 215 060
3. Практическая работа № 1
Сколько прошло дней, часов, минут, секунд с момента твоего рождения до сегодняшнего дня? (Для простоты вычислений считай день своего рождения и сегодняшний день полностью прожитыми днями.)
Ответы к странице 64
4. Практическая работа № 2
Узнай, сколько дней, часов, минут, секунд прожил кто-либо из твоих родных или друзей (по твоему выбору) с момента рождения до сегодняшнего дня.
5. В библиотеке три хранилища. В первом хранилище 15 789 книг, во втором на 2634 книги меньше, чем в первом, а в третьем в 6 раз меньше, чем в первых двух хранилищах вместе. Сколько всего книг в библиотеке?
1) 15789 — 2634 = 13155 (к.) — во втором хранилище
2) 15789 + 13155 = 28 944 (к.) — в 1 и 2 хранилище
3) 28 944 : 6 = 4 824 (к.) — в 3 хранилище
4) 28944 + 4824 = 33768 (к.) — всего в библиотеке
Ответ: 33768 книг.
6. Купили три отреза одинаковой ткани. В первом отрезе 7 м ткани, во втором – в 2 раза больше, чем в первом, а в третьем – на 5 м меньше, чем во втором. За все три отреза заплатили 43 200 р. Сколько стоит каждый отрез?
1) 7 * 2 = 14 (м) — во втором отрезке
2) 14 — 5 = 9 (м) — в третьем отрезке
3) 7 + 14 + 9 = 30 (м) — ткани всего
4) 43 200 : 30 = 1440 (р) — стоит метр ткани
5) 7 * 1440 = 10 080 (р) — стоит первый отрез
6) 14 * 1440 = 20160 (р.) — стоит второй отрез
7) 9 * 1440 = 12960 (р.) — стоит третий отрез
Ответ: 10 080 р., 20 160 р., 12 960 р.
7. Междугородний автобус должен проехать расстояние между двумя городами, равное 350 км, за 7 часов. Но первые два часа из за сильного дождя он ехал со скоростью на 5 км/ч меньше, чем предполагалось. С какой скоростью автобус должен проехать оставшийся путь, чтобы прийти в пункт назначения без опоздания?
1) 350 : 7 = 50 (км/ч) — должна быть средняя скорость автобуса
2) 50 — 5 = 45 (км/ч) — была скорость автобуса первые 2 часа
3) 45 * 2 = 90 (км) — проехал автобус за 2 часа
4) 350 — 90 = 260 (км) — осталось проехать автобусу за 5 часов
5) 260 : 5 = 52 (км/ч) — должна быть скорость автобуса в оставшиеся 5 часов
Ответ: 52 км/ч.
8. Олег пробежал 1 км за 5 мин. На сколько быстрее он пробежит это расстояние, если увеличит скорость на 50 м/мин?
1) 1000 : 5 = 200 (м/мин) — была скорость Олега.
2) 200 + 50 = 250 (м/мин) — стала скорость Олега.
3) 1000 : 250 = 4 (мин) — за это время пробежит Олег 1 км со скоростью 250 м/мин.
4) 5 — 4 = 1 (мин) — на 1 минуту быстрее пробежит.
Ответ: на 1 минуту.
9. Найди значение выражения 450 – 9 • x, если x = 0, 1, 6, 8, 9, 40. Какое наибольшее значение может принимать x?
10. Запиши множество делителей и множество кратных числа 32
11. Во сколько раз число A больше, чем число B:
A (35 302 – 28 394) • 1500 : 400 + 479 145
B 57 912 – 180 • (119 486 + 3964) : 3000
Решаем по действиям :
1) 35 302 — 28 394 = 6 908;
2) 1 500 : 400 = 3,75;
3) 6 908 — 3,75 = 6 904,25;
4) 6 904,25 + 479 145 = 486,049.25
1) 119 486 + 3 964 = 123 450;
2) 123 450 : 3 000 = 41,15;
3) 57 912 — 180 = 57 732;
4) 57 732 — 41,15 = 57, 690.85
А / В = 486,049,25 / 57,690.85 = 8,5
Ответ: в 8,5 раз.
12. Определи, какого данного не хватает для ответа на вопрос задачи. Подбери возможное значение и реши задачу.
а) Мама купила 4 кг гречки. Сколько денег она заплатила? (не хватает, — по 20 р/ кг)
4 * 20 = 80 (р) — заплатила мама.
Ответ: 80 рублей.
б) Турист прошел за день 24 км. Сколько времени он был в пути? (не хватает, — со скоростью 4 км/ч)
24 : 4 = 6 (ч) — был в пути.
Ответ: 6 часов.
в) Рабочий делает 3 детали в час. Сколько всего деталей он сделал? (не хватает, — он работал 8 часов)
3 * 8 = 24 (д.) — всего сделал.
Ответ: 24 детали.
г) Самолёт вылетел из Москвы в 9 ч 25 мин утра. В котором часу он приземлился в Новосибирске? (не хватает, — он летел 2 часа)
9 ч 25 мин + 2 ч = 11 ч 25 мин.
Ответ: в 12 часу.
Ответы к странице 65
1) Верно ли, что 1 л равен 1 м3? НЕТ
2) Верно ли, что масса арбуза может быть равна 5 кг? ДА
3) Верно ли, что скорость пешехода равна примерно 30 км/ч? НЕТ
4) Верно ли, что 7 км2 24 м2 больше по площади, чем 80 000 дм2 ДА
14. Игра «Волшебная гора» Вычисли и найди закономерность:
1 • 9 + 2 = 9 + 2 = 11
12 • 9 + 3 = 90 + 18 + 3 = 111
123 • 9 + 4 = 900 + 180 + 27 + 4 = 1111
1234 • 9 + 5 = 9000 + 1800 + 270 + 36 + 5 = 11111
12345 • 9 + 6 = 111111
123456 • 9 + 7 = 1111111
1234567 • 9 + 8 = 11111111
12345678 • 9 + 9 = 111111111
Сохранится ли данная закономерность для следующей строки?
Начерти кроссворд в тетради по клеточкам и заполни его.
1. Многоугольник. четырехугольник
2. Однозначное натуральное число. два
3. Равенство, содержащее переменную, значение котрой надо найти. уравнение
4. Единица измерения времени. час
5. Предложение, о котором можно сказать, верно оно или не верно. высказывание
6. Высказывание, содержащее в записи знаки > или <. неравенство
7. Результат сложения. сумма
8. Результат вычитания. разность
9. Единица измерения времени. год
10. Часть прямой. луч

4. Прибор для измерения времени. часы
5. Запись, состоящая из чисел, букв и знаков арифметических действий. выражение
11. Число, при подстановке которого в уравнение получается верное равенство. корень
12. Высказывание, со держащее знак =. равенство
13. Прибор для измерения массы. весы
14. Величина. масса
15. Равенство, устанавливающее взаимосвязь между величинами. формула
16. Способ счёта больших промежутков времени. календарь
17. Прямоугольный параллелепипед, измерения которого равны. куб
18. Результат деления. частное
19. Наименьшее трёхзначное число. сто
Ответы к странице 66
1. Продолжи ряд на два числа, сохраняя закономерность:
а) 0, 19, 38, 57, 76, 95
б) 318, 422, 526, 630, 734
в) 72 574, 72 561, 72 548, 72 535, 72522
г) 1, 9, 25, 49, 81, 121, 169, 225
д) 0, 2, 6, 12, 20, 30, 42, 44
е) 2, 3, 5, 8, 12, 17, 23, 30
2. Что общего в примерах каждого столбика? Объясни приёмы вычислений.
50 – 23 = 27
71 – 15 = 56
24 • 3 = 72
4 • 19 = 76
75 : 5 = 15
84 : 6 = 14
68 : 17 = 4
92 : 46 = 2
Общее то, что во всех столбиках выражения с одинаковыми математическими операциями.
3. Запиши на математическом языке:
а) переместительное свойство сложения и умножения;
б) сочетательное свойство сложения и умножения;
в) распределительное свойство умножения;
г) правило деления суммы на число;
д) правило вычитания числа из суммы;
е) правило вычитания суммы из числа. Объясни их смысл
4. Пользуясь свойствами арифметических действий, упрости выражения:
99 + 1 + а = 100 + a
34 – (27 + с) = 7 — c
8 • m • 3 = 24 * m
5 • х – 2 • х = 3 * x
16 + b + 9 = 25 + b
(d + 46) – 45 = d + 1
n • 25 • 4 = n * 100
9 • у + у = 10 * y
5. Вычисли наиболее удобным способом:
а) 32 + 34 + 36 + 38 = 70 + 70 = 140
б) 5 • 19 • 5 • 3 • 2 • 2 = 100 * 3 * 19 = 100 * 57 = 5700
в) 47 • 15 + 53 • 15 = 100 * 15 = 1500
г) (786 + 195) – 586 = 200 + 195 = 395
д) 903 – 672 – 28 = 903 — 700 = 203
е) 245 • 64 – 245 • 54 = 245 * 10 = 2450
а) У Ани а марок, а у Тани на с марок меньше. Сколько марок у Ани и Тани вместе?
б) Купили n слив. За обедом съели х слив, а за ужином – k слив. Сколько слив осталось?
в) Было d красных шариков и k синих. Их разделили поровну на 3 человек. Сколько шариков досталось каждому?
г) Артём пой мал а рыбок, а Юра – в 4 раза больше. На сколько рыбок меньше поймал Артём, чем Юра?
д) После того как в саду посадили 4 ряда вишен по t вишен в ряду, осталось посадить ещё m вишен. Сколько всего вишен должны посадить в саду?
Ответы к странице 67
7. Найди значения выражений:
б) 90 – у : 8, если у = 64
90 — 64 : 8 = 82
в) (75 + а) – (94 + b), если а = 25, b = 3
(75 + 25) — (94 + 3) = 100 — 97 = 3
8. Викторина «В мире музыки» Вычисли. Расшифруй фамилии известных композиторов. Узнай, в какое время и в какой стране они жили. Слушаешь ли ты их музыку?
17 + 8 = 25
25 : 5 = 5
5 * 13 = 65
65 − 9 = 56
56 : 7 = 8
Т = 8
64 : 8 = 8
8 * 20 = 160
160 − 90 = 70
70 : 14 = 5
5 + 129 = 134
И = 134
40 * 6 = 240
240 : 30 = 8
8 * 50 = 400
400 − 80 = 320
320 : 10 = 32
Р = 32
37 * 2 = 74
74 − 20 = 54
54 : 9 = 6
6 * 80 = 480
480 − 350 = 130
Ц = 130
50 − 14 = 36
36 : 6 = 6
6 + 194 = 200
200 : 40 = 5
5 * 9 = 45
А = 45
18 + 12 = 30
30 : 5 = 6
6 * 7 = 42
42 − 26 = 16
16 : 4 = 4
С = 4
62 + 19 = 81
81 : 9 = 9
9 * 70 = 630
630 − 30 = 600
600 : 200 = 3
К = 3
352 + 8 = 360
360 : 4 = 90
90 − 75 = 15
15 * 7 = 105
105 − 7 = 98
Ч = 98
100 : 25 = 4
4 + 76 = 80
80 − 48 = 32
32 * 10 = 320
320 : 2 = 160
Й = 160
3 * 39 = 117
117 + 3 = 120
120 : 4 = 30
30 − 6 = 24
24 * 4 = 96
М = 96
249 − 127 = 122
122 + 58 = 180
180 : 30 = 6
6 * 7 = 42
42 − 32 = 10
О = 10
40 * 80 = 3200
3200 : 100 = 32
32 + 76 = 108
108 : 4 = 27
27 * 3 = 81
В = 81
9. Разбей на классы и прочитай числа:
3609,
92820,
720053,
9113004,
50886999,
45012870,
5380024597,
12345678910,
376000000200.
3 609 − три тысячи шестьсот девять;
92 820 − девяносто две тысячи восемьсот двадцать;
720 053 − семьсот двадцать тысяч пятьдесят три;
9 113 004 − девять миллионов сто тринадцать тысяч четыре;
50 886 999 − пятьдесят миллионов восемьсот восемьдесят шесть тысяч девятьсот девяносто девять;
45 012 870 − сорок пять миллионов двенадцать тысяч восемьсот семьдесят;
5 380 024 597 − пять миллиардов триста восемьдесят миллионов двадцать четыре тысячи пятьсот девяносто семь;
12 345 678 910 − двенадцать миллиардов триста сорок пять миллионов шестьсот семьдесят восемь тысяч девятьсот десять;
376 000 000 200 − триста семьдесят шесть миллиардов двести.
10. а) Какое число идёт при счёте за числом 82 355, 739 999?
б) Какое число предшествует в натуральном ряду числу 3480, 26 000?
11. Запиши в виде суммы разрядных слагаемых числа 817, 3029, 53 082, 706 480.
817 = 800 + 10 + 7
3029 = 3000 + 20 + 9
53 082 = 50 000 + 3 000 + 80 + 2
706 480 = 700 000 + 6 000 + 400 + 80
Ответы к странице 68
12. Запиши цифрами числа:
а) 4 тыс. 549 ед. = 4 549
б) 8 тыс. 20 ед. = 8 020
в) 76 тыс. 9 ед. = 76 009
г) 318 тыс. 690 ед. = 318 690
д) 439 млн 972 тыс. 508 ед. = 439 972 508
е) 5 млн 2 тыс. 16 ед. = 5 002 016
ж) 29 млн 396 ед. = 29 000 396
з) 4 млн 7 тыс. = 4 007 000
13. Найди в таблице:
а) наибольшее четырёхзначное число; 9 999
б) наименьшее четырёхзначное число; 1 000
в) наименьшее трёхзначное число с цифрой 8 в разряде единиц; 108
г) наибольшее четырёхзначное число с цифрой 5 в разряде десятков; 9 959
д) наибольшее пятизначное число с цифрой 7 в разряде сотен; 99 799
е) наибольшее четырёхзначное число с разными цифрами; 9 876
ж) наименьшее четырёхзначное число с разными цифрами. 1 234
Ищем в таблице и выделяем/
14. Прочитай число 28 057 000 094. Какая цифра стоит в разряде единиц миллионов этого числа? Сколько в нём всего миллионов?
28 057 000 094 − двадцать восемь миллиардов пятьдесят семь миллионов девяносто четыре. Цифра 7 стоит в разряде миллионов. Всего в это числе 28057 миллионов.
15. Сравни с помощью знаков >, <, = :
4 003 > 999
5 300 > 5 299
7 425 < 74 000
82 016 < 82 106
16. Выполни действия. Проверь с помощью калькулятора.
а) 305 246 – 21 237 = 284009
б) 524 032 + 78 369 = 602401
в) 4 061 497 + 938 708 = 5 000 205
г) 80 000 425 – 536 842 = 79 463 583
д) 23 715 926 + 3 276 315 = 26992241
е) 944 502 483 – 25 360 157 = 919142326
ж) 726 524 996 + 873 475 104 = 1 600 000 100
з) 120 036 705 – 92 759 318 = 27 277 387
17. Составь программу действий и вычисли:
1 3 2 4
(9452 + 13 808) – (55 400 – 39 326) + 1 227 381 = 1 284 567
1) 9452 + 13 808 = 23 260
+ 9452
13808
23260
2) 55400 — 39326 = 16074
-55400
39326
16074
3) 23260 — 16074 = 7186
-23260
16074
7186
4) 7186 + 1 277 381 = 1 284 567
Ответы к странице 69
18. а) На сколько число 32 856 меньше числа 40 912?
б) На сколько число 51 045 больше числа 6387?
19. Найди неизвестные числа:
Слева: 98002 — 72 = 97 930
Справа: 5347 + 98 = 5447
20. Вычисли длину неизвестного отрезка, используя взаимосвязь между частью и целым.
а) 18 — ( 6 + 9) = 18 — 15 = 3 (см)
б) (23 + 29) — 36 = 16 (мм)
в) 7 + 14 +16 = 37 (дм)
г) 48 — 34 + 6 = 20 (м)
21. На отрезке MK длиной 26 см отметили точку A так, что AM = 19 см, и точку B так, что BK = 12 см. Найди длину отрезка AB.
19 + 12 — 26 = 31 — 26 = 5 (см) длина AB.
Ответ: 5 см.
22. Составь все возможные равенства из чисел 3409, 596, 4005. Как найти целое? Как найти часть?
3409 + 596 = 4005
596 + 3409 = 4005
4005 — 3409 = 596
4005 — 596 = 3409
23. Реши уравнения с комментированием и сделай проверку:
1) x – 18 910 = 3 459;
х = 3 459 + 18 910;
х = 22369.
Проверка:
22369 – 18 910 = 3 459;
3 459 = 3 459.
Ответ: х = 22369.
2) 6 207 + x = 50 000;
х = 50 000 – 6 207;
х = 43793.
Проверка:
6 207 + 43793 = 50 000;
50 000 = 50 000.
Ответ: х = 43793.
3) 45 180 – x = 7652;
х = 45 180 – 7 652;
х = 37528.
Проверка:
45 180 – 37528 = 7652;
7652 = 7652.
Ответ: х = 37528.
24. В автомобильных гонках участвовало три команды. У первой команды было 24 автомобиля, что на 3 автомобиля больше, чем у второй команды. Сколько автомобилей было у третьей команды, если всего в гонках участвовало 80 автомобилей?
1) 24 − 3 = 21 (авт.) − было у второй команды;
2) 24 + 21 = 45 (авт.) − было у первых двух команд;
3) 80 − 45 = 35 (авт.) − было у третьей команды.
Ответ: 35 автомобилей.
25. Стакан чая стоит 5 р., что на 12 р. дешевле, чем булочка. А чай вместе с булочкой стоят столько же, сколько апельсин. Сколько рублей надо заплатить за стакан чая, булочку и апельсин?
1) 5 + 12 = 17 (р.) — стоит булочка.
2) 17 + 5 = 22 (р.) — стоит апельсин.
3) 22 + 17 + 5 = 44 (р.) — надо заплатить за стакан чая, булочку и апельсин.
Ответ: 44 рубля.
Страница 70
26. Придумай задачу по схеме и реши её:
У ребят были конфеты: 18 карамельных конфет, шоколадных на 2 больше, с вафлей в три раза меньше, чем карамельных, а с черносливом столько сколько всех остальных видов вместе взятых. Сколько всего было конфет у ребят?
1) 18 + 2 = 20 (к.) было шоколадных.
2) 18 : 3 = 6 (к.) было с вафлей.
3) 18 + 20 + 6 = 44 (к.) было карамельных, шоколадных, и вафлей.
4) 44 + 44 = 88 (к.) было всего.
Ответ: 88 конфет.
27. а) Первая сторона треугольника равна 14 дм, а вторая сторона в 2 раза больше первой. Найди третью сторону треугольника, если его периметр равен 64 дм.
1) 14 * 2 = 28 (дм) — вторая сторона треугольника.
2) 64 — (14 + 28) = 22 (дм) — третья сторона треугольника.
Ответ: 22 дм.
б) Длина первой стороны треугольника 24 см. Это в 2 раза больше длины второй стороны и на 5 см меньше длины третьей. Найди периметр этого треугольника
1) 24 : 2 = 12 (см) вторая сторона треугольника.
2) 24 + 5 = 29 (см) третья сторона треугольника.
3) 24 + 12 + 29 = 65 (см) периметр прямоугольника.
Ответ: 65 см.
28. а) Ширина прямоугольника равна 84 м, что на 6 м меньше его длины. Найди периметр и площадь этого прямоугольника.
1) 84 — 6 = 78 (м) — длина прямоугольника.
2) 84 * 78 = 6552 (м 2 ) — площадь прямоугольника.
3) (84 + 72) * 2 = 312 (м) — периметр прямоугольника.
Ответ: 6552 м2 площадь и 312 м периметр.
б) Площадь прямоугольника равна 750 м2, а длина – 30 м. На сколько метров ширина этого прямоугольника меньше длины?
1) 750 : 30 = 25 (м) — ширина прямоугольника.
2) 30 — 25 = 5 (м) — на столько ширина этого прямоугольника меньше длины.
Ответ: на 5 метров.
29. Вычисли площади фигур:
а) 8 * 8 + 5 * 3 = 64 + 15 = 79 (м2) площадь фигуры.
Ответ: 79 м 2 .
б) 40 * 56 — 20 * 14 = 2240 — 280 = 1960 (см2) площадь фигуры.
Ответ: 1960 см 2 .
30. Построй квадрат со стороной 4 см. Затем построй прямоугольник, ширина которого на 2 см меньше, а длина – на 2 см больше стороны квадрата.
31. Длина классной комнаты 12 м, ширина 10 м, а высота 4 м. Найди её объём.
1) 12 *10 * 4 = 120 * 4 = 480 (м3) объем классной комнаты.
Ответ: 480 м 3 .
32. а) Вырази число 15 340
в десятках; 1534 дес.
в сотнях и единицах; 153 сотни 40 единиц
в тысячах и единицах. 15 тысяч 340 единиц
15 340 = 1534 дес. = 153 сот. 40 ед. = 15 тыс. 340 ед.
б) Вырази 15 340 см
в дециметрах; 1534 дм
в метрах и дециметрах. 153 метра 4 дм
15 340 см = 1534 дм = 153 м 4 дм
в) Вырази 15 340 м
в километрах и метрах. 15 км 340 м
15 340 м = 15 км 340 м
г) Вырази 15 340 г
в килограммах и граммах. 15 кг 340 г
д) Вырази 15 340 кг
в центнерах и килограммах; 153 ц 40 кг
в тоннах и килограммах. 15 т 340 кг
15 340 кг = 153 ц 40 кг = 15 т 340 кг
Страница 71
33. Вспомни таблицы мер длины, площади, объёма, массы. Выполни действия:
а) 5 м 96 см + 32 дм 4 см = 5 м + 96 см + 3 м + 24 см = 8 м + 1 м + 20 см = 9 м 20 см
б) 6 дм 3 см 2 мм – 48 см = 632 мм — 480 мм = 152 мм
в) 4 км 788 м + 6 км 20 м = 4788 м + 6020 м = 10 808 м
г) 12 км 52 м – 8 км 258 м = 12052 м — 8258 м = 3 км 794 м
д) 9 кг 200 г – 5 кг 540 г = 9 200 г — 5 540 г = 3 660 г = 3 кг 660 г
е) 17 ц 69 кг + 3 т 831 кг = 1769 кг + 3831 кг = 5600 кг = 5 т 6 ц
ж) 15 м2 2 см2 – 9 м2 5 дм2 27 см2 = 15 000 см2 + 2 см 2 — 9 000 см2 — 500 см 2 — 27 см2 = 5 475 см2
з) 12 дм3 – 3 дм3 4 см = 12 000 см3 — 3 000 см3 — 4 см3 = 9000 см3 — 4 см3 = 8 996 см3
34. Составь программу действий. Что ты замечаешь?
1 3 6 4 2 5
(a + b) · c – d : (k + m) · n
2 1 6 3 4 5
(a + b · c) – (d : k + m) · n
При одних и тех же условных единицах исчисления, получается разный порядок действий, то есть при реальных значениях будет разный результат.
35. Какие знаки арифметических действий можно поставить вместо звёздочек? Возможны ли другие варианты?
a * 0 = a (+ или -)
1 * a = a (*)
a * a = 1 (:)
a * 0 = 0 (*)
a * a = 0 (-)
a * 1 = a (* или 🙂
0 * a = 0 (* или 🙂
0 * a = a (+)
36. Составь программу действий и вычисли:
3 6 1 2 4 7 5
а) 24 : 1 – (4 • 5 – 14) • 4 + 8 : 8 = 1
1) 4 * 5 = 20
2) 20 — 14 = 6
3) 24 : 1 = 24
4) 6 * 4 = 24
5) 8 : 8 = 1
6) 24 — 24 = 0
7) 0 + 1 = 1
4 1 5 8 2 3 6 9 7
б) 0 • (15 – 6) : 3 + (7 • 8 + 4) : 60 – 1 • 0 = 1
1) 15 — 6 = 9
2) 7 * 8 = 56
3) 56 + 4 = 60
4) 0 * 9 = 0
5) 0 : 3 = 0
6) 60 : 60 = 1
7) 1 * 0 = 0
8) 0 + 1 = 1
9) 1 — 0 = 1
37. Составь 4 равенства из чисел 12, 5, 60. Прочитай эти равенства разными способами и построй графическую модель.
12 * 5 = 60
5 * 12 = 60
60 : 5 = 12
60 : 12 = 5
38. Реши уравнения c комментированием и сделай проверку:
б) 8 • x = 24 016
х = 24 016 : 8
х = 3 002
в) 351 900 : x = 5
х = 351 900 : 5
х = 70 380
39. Как умножить и как разделить круглые числа?
Нули можно не учитывать при вычислении, но учитывать в результате (если они стоят в конце)
а) 86 700 • 6 = 8670 : 6 * 10 = 1 445
в) 34 500 · 80 = 345 * 8 * 1000 = 2 760 000
д) 42 800 : 40 = 428 : 4 * 10 = 1070
ж) 21 063 000 : 700 = 210 630 : 7 = 30 090
б) 200 • 709 = 709 * 2 * 100 = 141 800
г) 5010 · 3000 = 501 * 3 * 10 000 = 1503 * 10 000 = 15 030 000
е) 260 400 : 50 = 26 040 : 5 = 5 208
з) 50 402 700 : 900 = 504027 : 9 = 56 003
40. Вычисли устно. Сделай проверку, используя формулу деления с остатком:
56 : 9 = 6 (ост. 2)
Проверка: 6 * 9 + 2 = 54 + 2 = 56
83 : 5 = 16 (ост. 3)
Проверка: 5 * 16 + 3 = 83
35 : 17 = 2 (ост. 1)
Проверка: 2 * 17 + 1 = 35
52 : 15 = 3 (ост. 7)
Проверка: 15 * 3 + 7 = 52
81 : 23 = 3 (ост. 12)
Проверка: 23 * 3 + 12 = 69 + 12 = 81
47 : 6 = 7 (ост. 5)
Проверка: 6 * 7 + 5 = 42 + 5 = 47
92 : 8 = 11 (ост. 4)
Проверка: 11 * 8 + 4 = 88 + 4 = 92
70 : 12 = 5 (ост. 10)
Проверка: 5 * 12 + 10 = 60 + 10 = 70
93 : 14 = 6 (ост. 9)
Проверка: 6 * 14 + 9 = 93
64 : 49 = 1 (ост. 15)
Проверка: 1 * 49 + 15 = 64
41. Выполни деление с остатком и сделай проверку:
б) 3275 : 3 = 1091 (ост. 2)
в) 40 153 : 5 = 8 030 (ост. 3)
-40153 |5
40 |8030
— 15
15
3
г) 603 240 : 9 = 67026 (ост. 6)
д) 840 260 : 80 = 10 503 (ост. 20)
-840260 | 80
80 |10503
— 4026
4000
-260
240
20
е) 360 450 : 60 = 6007 (ост. 30)
Ответы к странице 72
42. Сравни выражения, где буквы обозначают натуральные числа:
m + 48 < 80 + m
36 : x > 24 : x
60 – n > 25 – n
b : 5 < b : 3
k – 18 > k – 53
(9 + c) • 4 > 9 + c • 4
a + a + a > 2 • a
d • 6 – d = d • 5
43. Ворон живёт 60 лет, а овца – в 5 раз меньше ворона. Лошадь живёт на 4 года больше овцы, а хомяк – в 8 раз меньше лошади. Сколько лет живёт хомяк?
1) 60 : 5 = 12 (л.) — живет овца
2) 12 + 4 = 16 (л.) — столько лет живет лошадь
3) 16 : 8 = 2 (года) — столько лет живет хомяк
Ответ: хомяк живет 2 года.
44. Четыре зайчишки-братишки пошли в поле за морковками. Каждый из них принёс домой по 45 морковок. За ужином съели 36 морковок, а остальные разложили поровну в 3 пакета. Сколько морковок в каждом пакете?
1) 4 * 45 = 180 (м.) — принесли зайчишки
2) 180 — 36 = 144 (м.) — осталось после ужина
3) 144 : 3 = 28 (м.) — в каждом пакете
Ответ: 28 морковок.
45. В саду у Хрюши росла яблонька. Осенью он собрал урожай – 50 яблок. По 2 яблока Хрюша подарил 5 белочкам и по 3 яблока дал 3 ёжикам. Сколько яблок у него ещё осталось?
1) 2 * 5 = 10 (я.) — подарил белочкам
2) 3 * 3 = 9 (я.) — подарил ежикам
3) 10 + 9 = 19 (я.) — всего подарил
4) 50 — 19 = 31 (я.) — осталось
Ответ: 31 яблоко.
46. Бежала Мышка по полю и нашла 6 колосков по 40 зёрен в каждом. Чтобы испечь пирог, ей нужно 30 зёрен. Сколько пирогов сможет испечь Мышка из найденных колосков?
1) 6 * 40 = 240 (з.) — было в колосках
2) 240 : 30 = 8 (п.) — может испечь мышка
Ответ: 8 пирогов.
47. Белочка заготавливает грибы на зиму – каждый день одинаковое число грибов. За 5 дней она успела заготовить 40 грибов. Сколько грибов она сможет заготовить за неделю (7 дней)? За сколько дней она заготовит 200 грибов?
1) 40 : 5 = 8 (г.) — каждый день заготавливает белочка
2) 7 * 8 = 56 (г.) — белочка может заготовить за неделю
Ответ: 56 грибов.
48. Корней и Матвей подтянулись вместе 36 раз. Корней подтянулся на 14 раз меньше Матвея. Сколько раз подтянулся каждый из них?
1) 36 — 14 = 22 (р.) — подтянулись они поровну, если не учитывать 14 подтягиваний, на которые больше подтянулся Матвей
2) 22 : 2 = 11 (р.) — подтянулся Корней
3) 11 + 14 = 25 (р.) — подтянулся Матвей
Ответ: 11 раз подтянулся Корней и 25 раз Матвей.
49. Прошлым летом Пантелей собрал урожай абрикосов с трёх деревьев. С первого дерева он собрал 312 абрикосов, со второго – в 2 раза меньше, чем с первого, а с третьего – на 28 абрикосов больше, чем со второго. Из них 652 абрикоса съела коза Бориска, а остальные достались Пантелею. Сколько абрикосов ему досталось?
1) 312 : 2 = 156 (абр.) — собрал со второго дерева.
2) 156 + 28 = 184 (абр.) — собрал с третьего дерева.
3) 312 + 156 + 184 = 652 (абр.) — было собрано с трех деревьев.
652 = 652, то есть Пантелею ничего не достались.
Ответ: нисколько.
Страница 73
2) a – x = b
x = a — b
3) x – c = d
x = c + d
4) k + x = p
x = p — k
5) x : a = c
x = c * a
6) t • x = k
x = k : t
7) x • m = r
x = r : m
51. Прочитай выражения разными способами:
a + 3 • b
x : 2 – y
(c + d) • (m – n)
(8 • k) : (p + 4)
a + 3 • b
1) к а добавить произведение чисел 3 и b;
2) сумма чисел a и произведения чисел 3 и b.
x : 2 – y
1) из частного чисел х и 2 отнять у;
2) разность частного чисел х и 2 и y.
(c + d) • (m – n)
1) сумму чисел c и d умножили на разность чисел m и n;
2) произведение сумму чисел c и d и разности чисел m и n.
(8 • k) : (p + 4)
1) разность чисел a и 2 умножить на частное чисел b и 3;
2) произведение разности чисел a и 2 и частного чисел b и 3.
52. Реши уравнения с комментированием и сделай проверку:
а) 64 + 36 : (x • 3 – 15) = 70;
36 : (3х — 15) = 70 — 64;
36 : (3х — 15) = 6;
3х — 15 = 36 : 6;
3х — 15 = 6;
3х = 6 + 15;
3х = 21;
х = 21 : 3;
х = 7.
Проверка:
64 + 36 : (7 • 3 – 15) = 70;
70 = 70.
Ответ: х=7.
б) 124 – 24 • (480 : x – 56) = 28;
124 — 24•(480 : х — 56) = 28;
24•(480 : х — 56) = 124 — 28;
24•(480 : х — 56) = 96;
480 : х — 56 = 96 : 24;
480 : х — 56 = 4;
480 : х = 4 + 56;
480 : х = 60;
х — 480 : 60;
х = 8.
Проверка:
96 60 4
124 — 24•(480 : 8 — 56) = 28;
28 = 28.
Ответ: х=8.
53. Ваня задумал число, увеличил его в 7 раз, вычел 9, разделил на 6, к результату прибавил 15, разделил на 3 и получил 8. Какое число задумал Ваня?
Составим уравнение:
((x*7 — 9) : 6 + 15) : 3 = 8
((7x — 9) : 6 + 15) : 3 = 8
(7x — 9) : 6 + 15 = 24
(7x — 9) : 6 = 24 — 15
(7x — 9) : 6 = 9
7x — 9 = 54
7x = 54 + 9
7x = 63
x =9
Ответ: Ваня задумал число 9.
54. Найди произведения:
б) 279 • 42 = 11 718
в) 74 • 953 = 70 522
г) 506 • 125 = 63 250
д) 817 • 304 = 248 368
ж) 123 450 • 7800 = 962 910 000
з) 69 080 • 10 500 = 725 340 000
е) 608 • 207 = 125 856
55. Найди значения выражений:
а) (729 • 8 + 729 • 492) : 90 • (520 800 : 400 – 498) = 3 256 200
упростим выражение вынеся 729 за скобки
3 4 5 1 2
729 * (8 + 492) : 90 • (520 800 : 400 – 498) = 729 * 500 : 90 * (520 800 : 400 – 498) = 3 256 200
1) 520 800 : 400 = 1302
-520800 |400
400 |1302
— 1208
1200
— 800
800
0
2) 1302 — 498 = 804
3) 729 * 500 = 364 500
х729
500
364500
4) 364500 : 90 = 4050
-364500 |90
360 |4050
— 450
450
0
5) 4050 * 804 = 3 256 200
х4050
804
+ 1620
3240
3256200
5 1 6 8 7 3 2 4
б) 405 • (803 – 597) : 6 + 876 000 : (3104 – 72 • 38 + 432) = 15 000
1) 803 – 597 = 206
2) 72 • 38 = 2 736
3) 3104 — 2736 = 368
4) 368 + 432 = 800
5) 405 * 206 = 83430
х405
206
+ 2430
810
83430
6) 83430 : 6 = 13905
7) 876000 : 800 = 1095
-876000 |800
800 |1095
— 7600
7200
— 4000
4000
0
8) 13905 + 1095 = 15000
56. Составь выражения и найди их значения:
а) Белоснежка приготовила m порций мороженого. Из них n порций она отдала своему другу Медвежонку, а остальные разделила поровну между 7 гномами. Сколько порций мороженого получил каждый гном? (m = 17, n = 3)
Составим выражение:
(m — n) : 7, подставим значения.
(17 — 3) : 7 = 14 : 7 = 2 (мор.) получил каждый гном.
Ответ: 2 порции мороженного.
б) Чтобы добраться до замка Принцессы, Кот в сапогах преодолел m км. Первые n км он ехал на повозке. Остальной путь он шёл пешком в течение недели, проходя каждый день поровну. Сколько километров проходил Кот в сапогах за один день? (m = 500, n = 150)
Составим выражение:
(m — n) : 7, подставим значения.
(500 — 150) : 7 = 350 : 7 = 50 (км) в день проходил кот.
Ответ: 50 км.
Что общего и что различного в этих задачах?
Задачи решаются по одному алгоритму, с разными значениями.
Придумай свою задачу про сказочных героев, имеющую такое же решение.
Мама коза принесла домой 9 вилков капусты. 2 вилка она прибрала в подпол, а остальные раздала 7 козлятам. Сколько вилков досталось каждому?
ГДЗ к странице 74
57. Придумай задачи по таблицам:
Автомобиль ехал 2 часа со скоростью 60 км/ч, а потом 3 часа со скоростью 50 км/ч. Сколько за это время проехал автомобиль.
1) 2 * 60 = 120 (км) — проехал за 2 часа
2) 3 * 50 = 150 (км) — проехал за 3 часа
3) 120 + 150 = 270 (км) — проехал всего
Ответ: 270 км.
Станок выпускал детали с производительность 60 шт./ч в течение 2 часов, а потом 50 шт./ч в течение 3 часов. Сколько деталей он выпустил за это время?
1) 2 * 60 = 120 (дет.) — выпустил за 2 часа
2) 3 * 50 = 150 (дет.) — выпустил за 3 часа
3) 120 + 150 = 270 (дет.) — выпустили всего
Ответ: 270 деталей.
Что ты замечаешь? Придумай задачи с другими величина ми, которые решаются так же.
Задачи решаются по одному и тому же алгоритму, имеют одно и то же номинальное значение, но разные единицы измерения.
1. В первый день в магазине продали 2 кружки за 60 рублей, а во второй 3 за 50 рублей. Сколько выручили за кружки за два дня?
2. Коля собрал в лесу 2 корзинки по 60 грибов, а Леша 3 по 50 грибов. Сколько грибов собрали мальчики?
58. Велосипедист проехал расстояние 32 км за 2 ч. За сколько времени он проедет 80 км, если его скорость не изменится?
1) 32 : 2 = 16 (км/ч) — скорость велосипедиста
2) 80 : 16 = 5 (ч.) — надо велосипедисту, чтобы проехать 80 км
Ответ: 5 часов.
59. Катер проплыл расстояние 84 км за 3 ч, после чего ему осталось проплыть 140 км. За сколько времени он проплывёт оставшееся расстояние, если увеличит скорость на 7 км/ч?
1) 84 : 3 = 28 (км/ч) — была скорость катера
2) 28 + 7 = 35 (км/ч) — будет скорость катера
3) 140 : 35 = 4 (ч.) — надо будет катеру
Ответ: за 4 часа.
60. Мастер должен был изготовить 90 деталей за 6 ч. Однако он успевал сделать в час на 3 детали больше, чем предполагал. На сколько часов быстрее он сделал эту работу?
1) 90 : 6 = 15 (дет./ч.) — должна быть производительность мастера.
2) 15 + 3 = 18 (дет./ч.) — была на самом деле производительность мастера.
3) 90 : 18 = 5 (ч.) — понадобилось мастеру.
Ответ: 5 часов.
61. Лида и Оля купили тесьму на 48 р. каждая: Лида – по цене 8 р., а Оля – 12 р. за метр. Кто из них купил больше тесьмы и на сколько?
1) 48 : 8 = 6 (м) — купила Лида.
2) 48 : 12 = 4 (м) — купила Оля.
3) 6 — 4 = 2 (м) — на столько больше купила Лида
Ответ: на 2 метра больше купила Лида.
62. В летнем лагере «Орлёнок» отдыхало на 120 детей больше, чем в лагере «Следопыт». По окончании смены для отправки детей в город лагерю «Орлёнок» потребовалось 19 автобусов, а лагерю «Следопыт» – 14 таких же автобусов. Сколько детей отдыхало в этих лагерях, если в каждом автобусе ехало одинаковое количество детей?
1) 19 — 14 = 5 (авт.) — увезли 120 детей.
2) 120 : 5 = 24 (р.) — было в каждом автобусе.
3) 19 + 14 = 33 (авт.) — было всего.
4) 33 * 24 = 792 (р.) — всего отдыхало.
Ответ: 792 ребенка.
63. Автомобиль проехал с одинаковой скоростью в первый день 960 км, а во второй – 720 км. В первый день он был в пути на 3 ч больше, чем во второй день. Какое расстояние он проедет за 7 ч, двигаясь с той же скоростью?
1) 960 — 720 = 240 (км) — автомобиль ехал 3 часа.
2) 240 : 3 = 80 (км/ч) — скорость автомобиля.
3) 7 * 80 = 560 (км) — автомобиль проедет за 8 часов.
Ответ: 560 км.
64. Реши задачи и сравни их решения. Как называют такие задачи?
а) Для двух классов купили 8 одинаковых пачек учебников. Один класс получил 45 учебников, а другой – 75. Сколько пачек учебников получил каждый класс?
1) 45 + 75 = 120 (уч.) было всего.
2) 120 : 8 = 15 (уч.) было в пачке.
3) 45 : 15 = 3 (пач.) получил 1 класс.
4) 8 — 3 = 5 (пач.) получил 2 класс.
Ответ: 3 и 5 пачек получили классы.
б) Для двух классов купили 120 учебников в одинаковых пачках. Один класс получил 3 пачки, а другой – 5 пачек. Сколько учебников получил каждый класс?
1) 3 + 5 = 8 (п.) — купили всего.
2) 120 : 8 = 15 (уч.) — было в каждой пачке.
3) 3 * 15 = 45 (уч.) — получил один класс.
4) 5 * 15 = 75 (уч.) — получил второй класс.
Ответ 45 и 75 учебников получили классы.
Эти задачи называются взаимнообратные.
Ответы к странице 75
65. Вадим купил для себя 18 одинаковых тетрадей, а для соседа – 12 таких же тетрадей. За всю покупку он за платил 450 р. Сосед принёс ему купюру в 500 р. Сколько сдачи Вадим должен ему вернуть?
1) 18 + 12 = 30 (т.) — купил Вадим
2) 450 : 30 = 15 (р.) — стоит тетрадь
3) 12 *30 = 360 (р.) — Вадим отдал за тетради соседа
4) 500 — 360 = 140 (р.) — должен отдать сдачи
Ответ: 140 рублей.
66. Первый маляр за 3 ч покрасил потолок в комнате площадью 27 м2. Второй маляр, выполняя такую же работу, потратил на 2 ч больше времени. Но площадь его комнаты была на 13 м2 больше, чем у первого. У кого из них производительность больше и на сколько?
1) 27 : 3 = 9 (м 2 /ч) — производительность первого маляра.
2) 3 + 2 = 5 (ч) — потратил второй маляр.
3) 27 + 13 = 40 (м 2 ) — покрасил второй маляр.
4) 40 : 5 = 8 (м 2 /ч) — производительность второго маляра.
5) 9 — 8 = 1 (м 2 /ч) — на столько производительность первого маляра выше, чем второго.
Ответ: на 1 м 2 /ч.
67. Саше надо отметить точку М, нарисовать луч АК, отрезок ВС и прямую EF. На рисунке показан его чертёж. Какие ошибки он допустил? Нарисуй в тетради указанные фигуры правильно.
а) прямую АМ;
б) отрезок АМ;
в) луч АМ;
г) луч МА.
а) Отметь две точки А и В, проведи через них прямую. Начерти луч ОМ, пересекающий прямую АВ, и луч КС, её не пересекающий.
б) Отметь точки М и D и проведи луч DM. Начерти прямую EK, которая пересекает луч DM, и прямую АС, которая его не пересекает.
70. Построй отрезок AB = 5 см 4 мм и отметь на нём точки C и D так, чтобы точка C лежала между точками B и D. Измерь отрезок BC.
Строим отрезок, отмечаем точки. Получившиеся измерения могут быть самыми разными, поэтому измеряем конкретно для вашего случая.
71. Измерь с помощью линейки стороны многоугольника и найди его периметр. Сколько у него острых углов, прямых, тупых?
По нашим измерениям 18 см.
АВ = 4 см
ВС = 5 см
СD = 3 см
DE = 4 см
EA = 2 см
72. Найди в окружающей обстановке предметы, которые могут служить моделями отрезков. Рассмотри с помощью этих моделей возможные случаи взаимного расположения двух отрезков. Опиши их словами и изобрази на чертеже.
Стороны листа бумаги:
Плинтуса по полу:
Жерди (перемычки) в заборе:
Ответы к странице 76
а) Построй треугольник АВС. Построй треугольник, симметричный треугольнику АВС относительно стороны ВС. Перенеси полученный треугольник вправо на 8 клеточек. Опиши обратное преобразование.
б) Построй квадрат АВСD со стороной 3 см. Построй квадрат, симметричный ему относительно стороны СD.
а) Найди симметричные фигуры и укажи оси симметрии. Какими способами можно проверить правильность ответа?
б) Сколько осей симметрии имеют прямоугольник, квадрат, круг? Построй их и укажи оси симметрии.
Прямоугольник: 2. Квадрат: 4. Круг: бесконечное множество.
75. Выполни действия:
а) (3 мин 48 с + 16 мин 36 с – 6 мин 54 с) • 120 = (3 * 180 + 48 + 16 * 60 + 36 — 6 * 60 — 54 ) * 120 = (588 + 960 + 36 — 360 — 54) * 120 = 140 400 с = 2340 мин = 39 часов
б) (4 сут. 6 ч 15 мин – 18 ч 29 мин + 5 сут. 12 ч 14 мин) : 9 = (4 * 24 * 60 + 6 * 60 + 15 — 18 *60 — 29 + 5 * 24 * 60 + 12 * 60 + 14) : 9 = (5760 + 360 + 15 — 1080 — 29 + 7200 + 720 + 14) : 9 = 12960 : 9 = 1440 мин = 24 ч = 1 сут.
76. По таблице построй формулу зависимости y от x:
77. Подбери корни уравнений и сделай проверку:
а) х • х + 4 = 29;
х • х = 29 — 4;
х • х = 25;
x = 5.
Проверка:
5 • 5 + 4 = 29;
29 = 29.
Ответ: x = 5.
б) (х – 2) • (х + 5) = 0
произведение равно нулю, если хотя бы один множитель равен нулю
1) х — 2 = 0 (для того, чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое);
х = 0 + 2;
х = 2.
2) х + 5 = 0 (для того, чтобы найти неизвестное слагаемое, нужно от суммы вычесть известное слагаемое);
х = 0 — 5
Корня нет.
Пояснение от 7 гуру: на самом деле корень (-5), но в 3 классе дети еще не изучали отрицательные числа.
78. Как называется множество:
а) людей, обслуживающих самолёт в полёте; экипаж
б) фруктовых деревьев на пришкольном участке; сад
в) машин, движущихся по дороге; поток
г) верблюдов, идущих друг за другом по пустыне? караван
79. К – множество планет Солнечной системы. Принадлежит ли этому множеству Марс, Земля, Луна, Полярная звезда?
Марс, Земля, принадлежат множеству К, а вот Полярная звезда нет. Луну тоже нельзя отнести к множеству К, так как это спутник планеты, а не планета!
Страница 77
80. А – множество трёхзначных чисел, В – множество чисел, оканчивающихся цифрой 2. Принадлежат ли этим множествам числа: 724, 42, 531, 1022, 738, 63? Сделай записи, используя знаки
81. По диаграмме Эйлера–Венна определи, из каких элементов состоят множества А и В.
Составь множества А В и А В.
Сделай записи, используя знаки и:
82. А – множество букв в слове «море», D – множество букв в слове «дом», E – множество букв в слове «дым». Запиши элементы множеств: A, D, E, A⋂D, D⋂E, (A⋂D)⋂E, A⋂(D⋂E)
Элементы букв множества A
Элементы букв множества D
Элементы букв множества E
Элементы букв множества A⋂D
Элементы букв множества D⋂E
Элементы букв множества (A⋂D)⋂E
Элементы букв множества A⋂(D⋂E)
83. M = , K = , T = . Запиши элементы множеств: M∪K, K∪T, (M∪K)∪T, M∪(K∪T)
84. В коробке красные, синие, жёлтые и зелёные карандаши. Сколько существует различных способов выбора двух карандашей, если цвет карандашей:
а) должен быть различным;
б) может быть одинаковым?
а) Пусть:
K − красный цвет;
С − синий цвет;
Ж − желтый цвет;
З − зеленый цвет.
Тогда:
1) КС;
2) КЖ;
3) КЗ;
4) СЖ;
5) СЗ;
6) ЖЗ.
Ответ: 6 вариантов
б) Пусть:
K − красный цвет;
С − синий цвет;
Ж − желтый цвет;
З − зеленый цвет.
Тогда:
1) КС;
2) КЖ;
3) КЗ;
4) СЖ;
5) СЗ;
6) ЖЗ;
7) КК;
8) СС;
9) ЖЖ;
10) ЗЗ.
Ответ: 10 вариантов
85. На конкурсе чтецов Аня должна прочитать 3 стихотворения разных авторов. Она выбрала 2 стихотворения М. Ю. Лермонтова, 2 стихотворения А. Блока и три стихотворения А. С. Пушкина. Сколько программ своего выступления сможет составить Аня из этих стихов, если порядок их чтения не имеет значения
Пусть:
Б1 − первое стихотворение Блока;
Б2 − второе стихотворение Блока;
Л1 − первое стихотворение Лермонтова;
Л2 − второе стихотворение Лермонтова;
П1 − первое стихотворение Пушкина;
П2 − второе стихотворение Пушкина;
П3 − третье стихотворение Пушкина.
Тогда:
1) Б1, Л1, П1;
2) Б1, Л1, П2;
3) Б1, Л1, П3;
4) Б1, Л2, П1;
5) Б1, Л2, П2;
6) Б1, Л2, П3;
7) Б2, Л1, П1;
8) Б2, Л1, П2;
9) Б2, Л1, П3;
10) Б2, Л2, П1;
11) Б2, Л2, П2;
12) Б2, Л2, П3.
Ответ: 12 программ своего выступления сможет составить Инна из этих стихов.
86. Нарисуй в тетради кроссворд и заполни клетки арабскими цифрами:
По вертикали: По горизонтали:
а. XLV a. IV b. СDXVIII c. CLII k. CXXXIV
c. MCDXXVII m. DCXV n. DCCXXIX
d. MMDCIX
e. CCCLIV
t. XXI

87. Нарисуй в тетради кроссворд и заполни клетки римскими цифрами:
По вертикали: По горизонтали:
а. 1710 a. 2100
b 1211 d. 1800
c. 225 f. 340 d. 1400 k. 621
e. 151 m. 14
Ответы к странице 78
88. Легенда о шахматной игре
Игра в шахматы была придумана в Индии, и когда индусский царь Шерам по знакомился с нею, он был восхищён остроумием её создателя и разнообразием возможных в ней комбинаций.
Узнав, что она изобретена одним из его подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку.
Изобретатель, его звали Сета, явился к трону повелителя. Это был скромно одетый учёный, получавший средства к жизни от своих учеников. Я желаю достойно наградить тебя, Сета, за прекрасную игру, которую ты придумал, — сказал царь.
Мудрец поклонился.– Я достаточно богат, чтобы исполнить самое смелое твоё пожелание, – продолжал царь. – Назови награду, ко то рая тебя удовлетворит, и ты получишь её.
Сета молчал. – Не робей, – ободрил его царь. – Выскажи своё желание, я не пожалею ничего, чтобы исполнить его.
Когда Сета объявил наконец своё желание, он удивил царя беспримерной скромностью своей просьбы.– Повелитель, – сказал Сета, – прикажи вы дать мне за первую клетку шахматной доски одно пшеничное зерно, за вторую клетку – два зерна, за третью – 4 зерна, за четвёртую – 8 зёрен, за пятую – 16. – Довольно, – с раздражением прервал его царь, – ты получишь свои зёрна за все 64 клетки доски согласно твоему желанию: за каждую вдвое больше предыдущей. Но знай, что просьба твоя не достойна моей щедрости. Слуги мои вынесут тебе твой мешок с пшеницей.
Сета улыбнулся, покинул залу и стал дожидаться у ворот дворца. Вечером, от ходя ко сну, царь осведомился, давно ли Сета со своим мешком пшеницы покинул дворец.– Повелитель, – ответили ему, – математики твои трудятся без устали и надеются ещё до рассвета закончить подсчёт.– Почему медлят с этим делом? – гнев но воскликнул царь. – Завтра, прежде чем я проснусь, всё до последнего зерна должно быть выдано Сете. Я дважды не приказываю.
Утром старшина придворных математиков доложил царю результаты подсчёта.
Ответы к странице 79
Не в твоей власти, повелитель, исполнять подобные желания. Во всех амбарах твоих нет такого числа зёрен, которое потребовал Сета. Нет его и в житницах целого царства. Не найдётся такого числа зёрен и на всём пространстве Земли. И если желаешь непременно выдать обещанную награду, прикажи превратить царства в пахотные поля, прикажи растопить льды и снега, осушить моря и океаны и всё пространство их сплошь засеять пшеницей. И всё, что родится, отдать Сете. Тогда он получит свою награду. С изумлением внимал царь словам старца.– Назови же мне это чудовищное число! – воскликнул он.– Восемнадцать квинтильонов четыреста сорок шесть квадрильонов семьсот сорок четыре триллиона семьдесят три биллиона семьсот девять миллионов пятьсот пятьдесят одна тысяча шестьсот пятнадцать, о повелитель! Такова легенда. Действительно ли было то, что здесь рассказано, – неизвестно, но что награда, о которой говорит предание, должна была выразиться именно таким числом, в этом каждый может убедиться терпеливым подсчётом. Для этого нужно сложить числа 1, 4, 8 и т. д., результат 63-го удвоения покажет, сколько причиталось изобретателю за 64 клетки доски. Есть одно замечательное свойство чисел, которое позволяет облегчить вычисления: искомая сумма равна произведению 64 двоек, уменьшенному на 1. Образовав из множителей 6 групп по 10 двоек в каждой и одну группу из 4 двоек, получим, что искомое число равно:
1024 • 1024 • 1024 • 1024 • 1024 • 1024 • 16 – 1 = очееень много
Попробуй подсчитать.
89. Пользуясь заданным алгоритмом, найди значения х и сопоставь их соответствующим буквам. Расшифруй слово, расположив ответы примеров в порядке убывания:
| a | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| x | 44 | 34 | 50 | 40 | 56 | 46 | 62 | 52 |
| У | Ы | И | Л | А | К | К | Н |
Краткие ответы
Ответы для самопроверки
Урок 1. № 3. г) 18 км/ч. № 5. а) 168 км/ч. № 6. б) на 45 км/ч. № 7. б) 540. № 8. г) 504 600. № 9*. 44 ноги.
Урок 2. № 5. а) 32 км; б) 60 км/ч; в) 60 с = 1 мин. № 6. 50 км/ч. № 7. 68 дм2, 70 дм3. № 8. а) 16; б) 5; в) 30. № 9. D (11) = , K (11) = . № 10. б) 6 977 636. № 11*. б) Вторник.
Урок 3. № 4. а) 49 с; б) 640 м; в) 38 км/ч; г) 7 ч. № 5. а) 7; б) 34. № 9. а) 6; б) 8. № 12*. 8 гусей.
Урок 4. № 2. v = 180 : t. № 3. s = v · 5. № 4. t = 60 : v. № 5. а) Может; б) успеет. № 6. а) 60; б) 5; в) 40. № 10. б) с = 2, r = 0; в) с = 0, r = 2. № 11. б) 2 577 382 213; в) 222 540 000; г) 420 080. № 12*. в) 1 год.
Урок 5. № 1. в) s = 15 · t; d = 75 – 15 · t; D = 75 + 15 · t. № 2. б) s = 3 · t; d = 12 + 3 · t; D = 18 – 3 · t. № 4. 12 км; 2 ч. № 5. а) n : k; б) b · a; в) x : 5 – x : 6. № 8. а) 6; б) 70; в) 7. № 9. а) 240 270; б) 84 631 826. № 10*. Вт., ср., пт.
Урок 6. № 1. б) s = 80 · t; d = 480 – 80 · t; D = 160 + 80 · t. № 2. б) s = 60 · t; d = 360 – 60 · t; D = 120 + 60 · t. № 3. г) 750 030. № 4. 2 ч. № 5. 4 км/ч. № 6. а) 8; б) 60. № 8. D (14) = ; K (14) = .
Урок 7. № 2. 23 км/ч. № 3. в) 183 км. № 4. а) 60; б) 180; в) 5. № 8. D (15) = ; K (15) = .
Урок 8. № 1. в) На 2 км/ч. № 2. а) 20 мин. № 3. б) (а + (а + b)) : t; в) (а + а : b) : v. № 4. а) а : b + a : c, 8 ч; б) y : k – x : k, 1 км/ч; в) d : n · m, 420 км. № 6. а) 80 м2; б) 6560 см2. № 7. а) 3; б) 90. № 10*. а) 81; б) 99; в) 26.
Урок 9. № 1. б) 8 мин 20 с. № 2. б)18 км/ч. № 4. 110 км/ч. № 8. б) 9. №9. б) s = 6 · t; d = 30 – 6 · t; D = 30 + 6 · t.
Урок 10. № 1. а) 8016 м; 5009 мм; 2306 кг; 407 008 г. № 2. б) 20 км/ч. № 3. 54 м3; 48 дм2. № 4. 14 ч. № 6. б) 13. № 7. в) 9. № 8. а) 15; б) 190. № 9. в) n · 3 + m · 2; г) d – с · 5. № 12*. Дальше всех – Илья, ближе – Костя.
Урок 11. № 1. а) В 3 раза; б) на 15 км/ч. № 2. а) n · 4 + b; б) m – v · 2; в) s : 2 – s : 3. № 3. а) 1 ч 24 мин; б) 21 мин 35 с; в) 6 т 3 ц. № 4. а) 1; б) 10. № 5. б) 15. № 6. 150 см2. № 7. 2) 6 дм2, 1 м; 3) 1 м 74 см. № 14*. 10 сл.
Урок 12. № 4. ж) 112 048; з) 651 672. № 5. б) 16 мин. № 7. в) 17. № 9. б) 58 мин 58 с. г) 47 мин. № 10*. 7 способами.
Урок 13. № 3. С = 45 · n. № 4. n = 240 : a. № 5. Сумма – 880 694, разность – 871 514. № 6. в) 251 940; г) 1 927 658. № 7. 10 ч 20 мин. № 8. а) 35 мм, 35 см, 305 мм, 350 мм, 350 см. № 9. а) 4 км 6 м; б) 1 км 6 м.
Урок 14. № 1. з) 549 183. № 4. б) 160 р. № 5. 2 б., 400 р. № 6. а) 360; б) 5. № 7. 129 024 зн. № 8. б) 84 км. № 10. а) n + 17 = m, или m – n = 17, или n = m – 17; г) k : 5 = d, или k : d = 5, или k = d · 5. № 12. 4 094 971.
Урок 15. № 2. а) 2 700 000; г) 628 230 000. № 4. а) 682 200; б) 5 059 172. № 6. а) 48; б) 15. № 8. 30 р. № 12. Юра.
Урок 16. № 2. б) 12 с., 8 с. № 3. а) 182 р. № 4. 1320 р. № 6. в) 19 532 000; г) 20 755 200. № 7. а) 49; б) 24.
Урок 17. № 1. в) 196 460 000; г) 27 636 800. № 2. а) На 14 р.; б) в 3 раза. № 3. г) b · 5 – a · 6. № 4. 3 шт. № 5. б) 62.
Урок 18. № 4. ж) 3 585 012; з) 7 401 205. № 6. б) 50. № 7. в) у · 4 – х · 2; д) (k : 3) · 8. № 8. а) 12 ч. № 12*. 1749 г.
Урок 19. № 2. а) 391 941; в) 55 016; д) 247 749; з) 95 930. № 5. б) 1200 р. № 7. б) 9 км 788 м; в) 25 дм2 74 см2; г) 7 т 667 кг; е) 5 мин 37 с. № 8. в) 5. № 9. 263 053. № 12*. 96 см2. № 13*. Равны; обе – шестые части числа. № 14*. 6 к.
Урок 20. № 2. а) 304 008; в) 203 907; г) 15 861 120. № 5. 400 р. № 6. б) d = 480 – 80 · t. № 7. На 15 км/ч. № 9. а) k : 5 – n : 9; б) (а + b) : 2 – а : 3; в) d : 4 + m; г) s : 2 – s : 5. № 10. а) 1 030 500; в) 64 720 000. № 12*. А В = ; 9.
Урок 21. № 4. б) 1800 б./ч. № 6. t = 36 : w. № 7. б) 297 168; г) 235 431. № 9. а) 348 192; б) 727 234. № 11. б) 270.Урок 22. № 1. На 4 стр./ч. № 2. б) 468 м. № 3. б) 192 д. № 4. 12 д. № 6. г) 76 140. № 8. 195 976. № 9. а) 30; б) 50.Урок 23. № 2. г) 120 м./д. № 4. 8 ч. № 5. б) На 20 р.; г) на 20 м3/ч. № 8. а) 3 км 234 м 2 дм; г) 2 т 166 кг 8 г; д) 2 сут. 4 ч 30 мин; е) 30 сут. № 9. 3 дм. № 10. а) V = 32 · с; в) V = S · h. № 11. б) y = x + 4. № 12*. Е.
Урок 24. № 2. г) 8 юб.; 6 юб. № 3. б) 36 км/ч. № 4. а) 1 869 400; б) 5087. № 8*. . № 9*. 2 д., 4 д., 1 д., 2 д., 2 д.
Урок 25. № 1. а) 9; б) 336. № 2. а) d : (m : 4); в) k : 6 + n; г) (a – b) : t. № 4. в) 1 ч 14 мин; г) 2 м 3 см 4 мм. № 5. На 4 куста. № 6. 384 м; 416 м. № 7. б) 12 000. № 8. 1 976 170, 43 092 000, 39 785 100; 45 068 170 и 41 115 830. № 11*. 8 к.
Урок 26. № 2. 252 кг. № 3. 64 кв. № 4. 17 ч. № 5. 960 р.; 640 р. № 7. б) 119 856; в) 33 830 000; г) 23 284 800; д) 80 700; е) 30 050. № 8. а) 6 696 390; б) 26 617 461 000. № 9*. 2 310 000, 2 650 692, 386 568.
Урок 27. № 2. 14 к./день, 280 к. № 3. а) (х +19) · 5 – 16 = 139, х = 12. № 4. б) 31. № 5. б) 320 943; г) 45 568 000; е) 81 631 200. № 6. б) 5 мин 27 с; г) 8 кг. № 7. 516 чел. № 8. 7 м. № 12*. а) 75, 90, 105; б) 36, 49, 64.
Урок 28. № 2. а) 14 781 264; б) 628 381 600; в) 69 215 060. № 5. 33 768 кн. № 7. 52 км/ч. № 11. В 10 раз.
Повторение: № 1. в) 72 535, 72 522; г) 169, 225; д) 42, 56; е) 23, 30. № 6. в) (d + k) : 3; д) t · 4 + m. № 17. 1 234 567. № 21. 5 см. № 23. а) 22 369; б) 43 793; в) 37 528. № 24. 35 ав. № 27. б) 65 см. № 28. а) 348 м, 7560 м2; б) 5 м. № 29. а) 79 м2; б) 1960 см2. № 31. 480 м3. № 33. г) 3 км 794 м; е) 5 т 6 ц; з) 8 дм3 996 см3. № 38. а) 36 504; б) 3002; в) 70 380. № 41. д) 10 503 (ост. 20). № 43. 2 года. № 44. 48 м. № 45. 31 яб. № 46. 8 п. № 47. 56 гр.; 25 д. № 48. К. – 11 раз, М. – 25 раз.№ 49. 0 абрикосов. № 52. а) 7; б) 8. № 53. 9. № 54. б) 11 718; в) 70 522; г) 63 250; д) 248 368; е) 125 856; ж) 962 910 000; з) 725 340 000. № 55. а) 3 256 200; б) 15 000. № 58. 5 ч. № 59. 4 ч. № 60. На 1 ч. № 61. Лида, на 2 м. № 62. 456 чел., 336 чел. № 63. 560 км. № 65. 320 р. № 66. У первого; на 1 м2/ч. № 75. а) 1 сут. 3 ч; б) 1 сут. № 76. а) у = х + 9; б) у = х · 9. № 77. а) 5; б) 2. № 78. а) Экипаж; б) сад; в) поток машин; г) караван. № 79. Марс ∈ K; Земля ∈ K; Луна ∉ K; Полярная звезда ∉ K. № 84*. а) 6 сп.; б) 10 сп. № 85*. 12 сп
Задачи на движение с примерами решения
2) скорость тела при движении по течению реки равна , а при движении против течения равна , где — собственная скорость тела (скорость в стоячей воде); — скорость течения реки; плот движется со скоростью течения реки.
При составлении уравнений в задачах на движение часто используются следующие очевидные утверждения:
1) если два тела, находящиеся перед началом движения на расстоянии , движутся навстречу друг другу со скоростями и , то время, через которое они встретятся, равно
2) если два тела, находящиеся перед началом движения на расстоянии , движутся в одном направлении со скоростями и , где , то время, через которое второе тело (его скорость ) догонит первое, равно .
Примеры с решениями
Пример №194.
Пешеход и велосипедист отправляются одновременно из пункта в пункт . В пункте велосипедист поворачивает обратно и встречает пешехода через 20 мин после начала движения. Не останавливаясь, велосипедист доезжает до пункта , поворачивает обратно и догоняет пешехода через 10 мин после первой встречи. За какое время пешеход пройдет путь от до ?
Решение:
Пусть и — скорости (в километрах в час) соответственно пешехода и велосипедиста, — путь (в километрах) . Так как пешеход и велосипедист встретились через ч, пройдя вдвоем путь , то
За полчаса, истекших от начала движения до того момента, когда велосипедист догнал пешехода, разность пройденных ими расстояний была равна , т. е.
Запишем систему уравнений (1), (2) в виде f Vi + vo = 6s,
и вычтем из первого уравнения системы (3) второе. Получим , откуда найдем искомую величину
Пример №195.
Пристань находится выше по течению реки, чем пристань . Из и одновременно навстречу друг другу начали движение плот и моторная лодка. Достигнув пристани , моторная лодка немедленно повернула обратно и догнала плот в тот момент, когда он проплыл расстояния между и .
Найти время, которое затрачивает плот на путь из в , если моторная лодка проплывает из в и обратно за Зч.
Решение:
Пусть — расстояние между пунктами и , и — скорость течения реки, — скорость моторной лодки в стоячей воде. Тогда

Полагая запишем систему (4) в виде

Первое из уравнений системы (5) приводится к однородному уравнению откуда Подставив это выражение во второе уравнение системы (5), получаем откуда
Пример №196.
Из пункта в пункт вышел пешеход. Вслед за ним через 2 ч из пункта выехал велосипедист, а еще через 30 мин — мотоциклист. Все участники движения перемещались равномерно и без остановок.
Через некоторое время после выезда мотоциклиста оказалось, что все трое преодолели одинаковую часть пути от до . На сколько минут раньше пешехода прибыл в пункт велосипедист, если пешеход прибыл туда на 1 ч позже мотоциклиста?
Решение:
Первый способ. Пусть — точка на пути , в которой одновременно оказались участники движения, , ; , , — скорости пешехода, велосипедиста и мотоциклиста соответственно, — искомое время. Используя условия задачи, составляем систему уравнений

Далее, из (6) получаем
и следовательно ,

Второй способ. Рассмотрим координатную плоскость, по оси абсцисс будем откладывать время , а по оси ординат — пройденный путь (рис. 17.1).
Пусть отрезки — графики движения пешехода, велосипедиста и мотоциклиста соответственно. По условию эти отрезки имеют общую точку с ординатой , точки лежат на прямой где — искомое время.
Так как то откуда
Пример №197.
Автомобилист и велосипедист, выехавшие одновременно соответственно из пунктов и , совершают безостановочное движение между этими пунктами. Доехав до пункта и повернув назад, автомобилист догнал велосипедиста через ч. после их первой встречи. Сколько времени после первой встречи ехал велосипедист до пункта , если к тому моменту, когда его обогнал автомобилист, он проехал пути от до ?
Решение:
Первый способ. Пусть — расстояние между пунктами и , и — скорости автомобиля и велосипедиста соответственно, — время (в часах) от начала движения до первой встречи. Тогда

Требуется найти величину Разделив почленно уравнения (10) и (9), получим
Из (8) и (11) следует, что
Наконец, из равенств (12) и (13) получаем и
Следовательно,
Ответ. 8 ч 45 мин.
Второй способ. Решим задачу, не составляя систему уравнений. От начала движения до того момента, когда автомобилист обогнал велосипедиста, они проехали и — пути от до . Поэтому отношение их скоростей равно
Следовательно, к моменту первой встречи участники движения проехали и пути от до . Но, затратив на дорогу еще ч, велосипедист проезжает всего пути. Значит, за 1ч он проезжает пути. Оставшуюся после первой встречи часть пути велосипедист проедет за
Пример №198.
Дорога проходит через пункты и . Велосипедист выехал из по направлению к . Одновременно с ним из пункта вышли с равными скоростями два пешехода: первый — в пункт , а второй — в противоположном направлении. Велосипедист проехал от до за 0,5ч и, продолжая движение, догнал второго пешехода. Это произошло через 1,2 ч после встречи велосипедиста с первым пешеходом. Определить время движения велосипедиста от начала движения до встречи с первым пешеходом.
Решение:
Пусть — место встречи велосипедиста с первым пешеходом (рис. 17.2).

Пусть — скорость велосипедиста, — скорость каждого из пешеходов. Тогда искомое время
Согласно условию задачи имеем
где — место (пункт), где велосипедист догнал второго пешехода, вышедшего из (в направлении ). Так как велосипедист и первый пешеход вышли одновременно, то время, в течение которого они находились в пути до встречи в , составляет
Расстояние велосипедист преодолел за ч, а второй пешеход за это время прошел км со скоростью . Следовательно,
Уравнение (16) в силу (14) и (15) можно записать так:
Аналогично, используя равенства (14) и (15), преобразуем уравнение (17):
Из (18) и (19) следует, что
откуда
Пример №199.
Из пунктов и навстречу друг другу вышли одновременно два поезда. Каждый из них двигался сначала равноускоренно (начальные скорости поездов равны нулю, ускорения различны), а затем, достигнув некоторой скорости, — равномерно. Отношение скоростей равномерного движения поездов равно . В момент встречи поезда имели равные скорости, а в пункты и прибыли одновременно. Найти отношение ускорений поездов.

Решение:
Пусть и — скорости равномерного движения первого и второго поездов, и — их ускорения. Предположим, что , тогда
Графики скоростей поездов как функций времени изображены на рис. 17.3.
Здесь и — время равноускоренного движения поездов, — момент их встречи, — время прохождения пути каждым из поездов. Заметим, что а так как и в момент поезда имели равные скорости.
Из равенств и условия (20) следует, что
Таким образом, для решения задачи нужно найти отношение
По условию в момент поезда имели равные скорости. Следовательно,
Из (22) и (20) находим
Пусть — все расстояние, пройденное каждым из поездов, тогда величина равна площади каждой из трапеций и (рис. 17.3), т. е.
Из равенств (24), (25) и (20) находим
Итак, получены уравнения (23) и (26), связывающие и . Не хватает еще одного уравнения. Такое уравнение (и в этом ключ к решению задачи) мы получим, заметив, что сумма расстояний и , пройденных поездами до встречи, равна .
![]()
Из (24), (27) и (23) следует, что т.е.
а из (26) и (28) получаем
Наконец, из равенств (21) и (29) находим, что
Ответ.
Пример №200.
Два велосипедиста движутся по кольцевой велотрассе длины , часть которой проходит по стадиону, а оставшаяся часть — по городским улицам. Скорость первого велосипедиста на стадионе равна , а на городских улицах равна . Скорость второго велосипедиста на стадионе равна , а на городских улицах . Велосипедисты одновременно въезжают на стадион. Через какое время после этого один из них впервые совершит обгон другого?
Решение:
Первый велосипедист проезжает полный круг за время

а второй — за время
Поэтому второй велосипедист догонит первого, если проедет на круг больше, чем первый, причем это произойдет на стадионе, поскольку там скорость второго больше, чем у первого.
Пусть — время от начала движения до момента, когда второй совершит обгон первого; — число целых кругов, пройденных до обгона вторым велосипедистом; — часть пути по стадиону, пройденная велосипедистами после кругов, пройденных вторым.
Так как на полный круг первый затрачивает на больше, чем второй, то второй, отрываясь от первого, догонит первого, когда выигрыша во времени будет достаточно, чтобы второй проехал круг. Поэтому второму достаточно проехать полных кругов чтобы затем на стадионе обогнать первого. Из условия равенства времени движения каждого его участника с учетом пройденного пути получаем систему уравнений

откуда (при ) находим

Ответ.
Пример №201.
Катер по реке и автобус по дороге, идущей вдоль берега реки, отправляются одновременно из пункта А в пункт В и совершают безостановочное движение между А и В. Первая их встреча произошла, когда автобус прошел — всего расстояния от А до В, а вторая встреча — когда автобус после первого захода в В проехал всего расстояния от В до А. Первый раз в пункт В автобус прибыл на 16 мин позже катера. Через сколько часов после начала движения автобус и катер окажутся одновременно в пункте А, если скорость катера в неподвижной воде и скорость автобуса постоянны ?
Решение:
Первый способ. Пусть и — время (в часах), за которое проходят путь АВ автобус и катер соответственно, a время, за которое катер проходит путь ВА, — расстояние АВ.
До первой встречи в пункте С автобус прошел путь за время . Такое же время катер затратил на АВ и путь ВС, равный . Следовательно,
До второй встречи автобус затратил время а катер — время (на АВ), затем (на ВА) и еще — . Значит,
По условию, автобус первый раз прибыл в В на 16 мин (на ч) позже катера, т. е.
Решив систему (30)-(32) находим
Автобус оказывается в пункте А, преодолев (четное число раз) путь от А до В и затратив время . Катер окажется в пункте А, совершив рейсов от А до В и рейсов от В до А и затратив время Одновременно в пункте А автобус и катер окажутся лишь в том случае, когда найдутся и такие, что т. е.
Так как 12 и 5 — взаимно простые числа, то число является целым только в том случае, когда делится на 5. Наименьшее возможное число и тогда
Итак, автобус и катер первый раз одновременно окажутся в пункте А, если автобус сделает рейсов (катер—12) и затратит время
Ответ. Через 4 ч.
Второй способ. Пусть — скорости соответственно катера в стоячей воде, автобуса и течения реки, — расстояние от А до В (река течет от А к В, скорость — в километрах в минуту). Тогда, учитывая, что до первой и второй встречи катер и автобус затратили одинаковое время, получаем

Так как катер пришел в пункт В на 16 мин раньше автобуса, то
Введем следующие обозначения:
Тогда система (33)—(35) примет вид

Линейная система (36) имеет решение Время, затраченное катером на путь от А до В и обратно, равно (мин), а время, затраченное автобусом на тот же путь, равно Одновременно автобус и катер первый раз окажутся в пункте А через целое число поездок, поэтому искомое время есть наименьшее общее кратное чисел 48 и 20 и равно 240 мин, т. е. 4 ч.
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Задачи на движение для 4 класса — формулы и примеры решений
Существует несколько типов задач на движение. Примеры решения всех типов задач с пояснениями мы рассмотрим в этой статье.
Задачи на движение в одном направлении
Задачи на движении в одном направлении относятся к одному из трех основных видов задач на движение.
Если два объекта выехали из одного пункта одновременно, то, поскольку они имеют разные скорости, объекты удаляются друг от друга. Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:
Если из одного пункта выехал один объект, а спустя некоторое время в том же направлении вслед за ним выехал другой объект, то они могут как сближаться, так и удаляться друг от друга.
Если скорость объекта, движущегося впереди, меньше движущегося вслед за ним объекта, то второй догоняет первого и они сближаются.
Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:
Если скорость объекта, который идет впереди, больше скорости объекта, который движется следом, то второй не сможет догнать первого и они удаляются друг от друга.
Скорость удаления находим аналогично — из большей скорости вычитаем меньшую:
Задачи на скорость сближения
Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?
Решение :
Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалится от города на:
Второй автомобиль движется быстрее первого, значит каждый час расстояние между автомобилями будет сокращаться на разность их скоростей:
60 — 40 = 20 (км/ч) – это скорость сближения автомобилей
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся:
Решение задачи по действиям можно записать так:
1) 40 · 4 = 160 (км) – расстояние между автомобилями
2) 60 — 40 = 20 (км/ч) – скорость сближения автомобилей
Ответ: Второй автомобиль догонит первый через 8 часов.
Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов:
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого:
Решение задачи по действиям можно записать так:
1) 5 — 4 = 1 (км/ч) – это скорость сближения пешеходов
Ответ: Через 5 часов второй пешеход догонит первого.
Из одного села в одном направлении одновременно выехали два велосипедиста. Скорость одного из них — 15 км/ч, скорость другого — 12 км/ч. Какое расстояние будет через ними через 4 часа?

Решение:
1) 15-12=3 (км/ч) скорость удаления велосипедистов
2) 3∙4=12 (км) такое расстояние будет между велосипедистами через 4 часа.
Ответ: Через 4 часа расстояние между велосипедистами составит 12 км.
Задача 4
Из села на станцию одновременно вышел пешеход и выехал велосипедист. Через 2 часа велосипедист опережал пешехода на 12 км. Найти скорость пешехода, если скорость велосипедиста 10 км/ч.

Решение:
1) 12:2=6 (км/ч) скорость удаления велосипедиста и пешехода
2) 10-6=4 (км/ч) скорость пешехода.
Ответ: Скорость пешехода составляет 4 км/ч.
Задачи на скорость удаления
Задача 1
Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.
Решение:
Сначала узнаем скорость удаления автомобилей друг от друга, для этого вычтем из большей скорости меньшую:
Каждый час автомобили отдаляются друг от друга на 40 км. Теперь можно узнать сколько километров будет между ними через 3 часа, для этого скорость удаления умножим на 3:
Чтобы узнать через сколько часов расстояние между автомобилями станет 200 км, надо расстояние разделить на скорость удаления:
Ответ:
Если два объекта движутся навстречу друг другу, то они сближаются. Чтобы найти скорость сближения двух объектов, движущихся навстречу друг другу, надо сложить их скорости:
Скорость сближения больше, чем скорость каждого из них.
Из поселка и города навстречу друг другу, одновременно выехали два автобуса. Один автобус до встречи проехал 100 км со скоростью 25 км/час. Сколько километров до встречи проехал второй автобус, если его скорость 50 км/час.
1) 100 : 25 = 4 (часа ехал один автобус)
2) 50 * 4 = 200
Решение в виде выражения: 50 * (100 : 25) = 200
Ответ: второй автобус проехал до встречи 200 км.
Расстояние между двумя пристанями 90 км. От каждой из них одновременно навстречу друг другу вышли два теплохода. Сколько часов им понадобится чтобы встретиться, если скорость первого 20 км/час, а второго 25 км/час?
1) 25 + 20 = 45 (сумма скоростей теплоходов)
Решение в виде выражения:90 : (20 + 25) = 2
Ответ: Теплоходы встретятся через 2 часа.
От двух станций, расстояние между которыми 564 км., одновременно навстречу друг другу вышли два поезда. Скорость одного из них 63 км/час. Какова скорость второго, если поезда встретились через 4 часа?
1) 63 * 4 = 252 (прошел 1 поезд)
2) 564 — 252 =312 (прошел 2 поезд)
Решение в виде выражения (63 * 4 — 252) : 4 = 78
Ответ: Скорость второго поезда 78 км/час.
Задача 4
Два велосипедиста выехали навстречу друг другу. Скорость одного из низ 12 км/ч, а другого — 10 км/ч. Через 3 часа они встретились. Какое расстояние было между ними в начале пути?
Решение:
1) 12+10=22 (км/ч) скорость сближения велосипедистов
2) 22∙3=66 (км) было между велосипедистами в начале пути.
Ответ: Расстояние между велосипедистами в начале пути было 66 км.
Два поезда идут навстречу друг другу. Скорость одного из них 50 км/ч, скорость другого — 60 км/ч. Сейчас между ними 440 км. Через сколько часов они встретятся?
Решение:
1) 60+50=110 (км/ч) скорость сближения поездов
2) 440:110=4 (ч) время, через которое поезда встретятся.
Ответ: Поезда встретятся через 4 часа.
Движение в противоположных направлениях
Если два объекта движутся в противоположных направлениях, то они удаляются. Чтобы найти скорость удаления, надо сложить скорости этих объектов:
Скорость удаления больше скорости любого из них.
Из поселка вышли одновременно в противоположных направлениях два пешехода. Средняя скорость одного пешехода – 5 км/ч, другого – 4 км/ч. Через сколько часов расстояние между ними будет 27 км ?
Чтобы найти время движения пешеходов, нужно знать расстояние и скорость пешеходов. Мы знаем, что за каждый час один пешеход удаляется от поселка на 5 км, а другой пешеход удаляется от поселка на 4 км. Можем найти их скорость удаления.
1. (км/ч)
Мы знаем скорость удаления и знаем все расстояние – 27 км. Можем найти время, через которое пешеходы удалятся друг от друга на 27 км, для этого нужно расстояние разделить на скорость.
2. (ч)
Ответ: Через три часа расстояние между переходами будет 27 км.
Из поселка вышли одновременно в противоположных направлениях два пешехода. Через 3 часа расстояние между ними было 27 км. Первый пешеход шел со скоростью 5 км/ч. С какой скоростью шел второй пешеход ?
Чтобы узнать скорость второго пешехода, надо знать расстояние, которое он прошел, и его время в пути. Чтобы узнать, какое расстояние прошел второй пешеход, надо знать, какое расстояние прошел первый пешеход и общее расстояние. Общее расстояние мы знаем. Чтобы найти расстояние, которое прошел первый пешеход, надо знать его скорость и его время в пути. Средняя скорость движения первого пешехода – 5 км/ч, его время в пути – 3 часа. Если среднюю скорость умножить на время в пути, получим расстояние, которое прошел пешеход:
1. (км)
Мы знаем общее расстояние и знаем расстояние, которое прошел первый пешеход. Можем теперь узнать, какое расстояние прошел второй пешеход.
2. (км)
Теперь мы знаем расстояние, которое прошел второй пешеход, и время, проведенное им в пути. Можем найти его скорость.
3. (км/ч)
Ответ: Скорость второго пешехода – 4 км/ч.
Товарный и пассажирский поезда движутся в противоположных направлениях. Скорость товарного 45 км/ч, скорость пассажирского — 70 км/ч. Сейчас между ними 20 км. Какое расстояние будет между ними через 2 часа ?

1) 70+45=115 (км/ч) скорость удаления поездов
2) 115∙2=230 (км) пройдут поезда вместе за 2 часа
3) 230+20=250 (км) такое расстояние между поездами будет через 2 часа.
Ответ: Через 2 часа расстояние между поездами составит 250 км.
Из одного пункта одновременно в противоположных направлениях выехали два мотоциклиста. Скорость одного из них — 60 км/ч, скорость другого — 40 км/ч. Через какое время расстояние между ними станет равным 300 км?

1) 60+40=100 (км/ч) скорость удаления мотоциклистов
2) 300:100=3 (ч) через такое время расстояние между ними будет 300 км.
Ответ: Расстояние между мотоциклистами станет 300 км через 3 часа.
Источники:
https://egemaximum.ru/13-5/
https://7gy.ru/gdz/matematika-otvety/3803-gdz-matematika-3-klass-uchebnik-3-chast-peterson.html
https://9219603113.com/zadachi-na-dvizhenie-s-primerami-resheniya/
https://sprint-olympic.ru/uroki/matematika-uroki/93258-zadachi-na-dvijenie-dlia-4-klassa-formyly-i-primery-reshenii.html



