Скорость велосипеда: средняя, максимальная, рекордная в км/ч

Однако многие задаются вопросом, какую скорость может развить велосипедист в различных условиях? Вне зависимости от причин, мы попробуем ответить на этот вопрос и разобраться с факторами, влияющими на скорость передвижения.
Скоростной тест
Рассмотрим показатели наиболее распространенных типов велосипедов – горный, шоссейный и городской, а также их промежуточных «братьев» — гибрид и туристический велосипед.

Другие типы предназначены не для быстрой езды, поэтому в сравнении не участвуют. Для интереса добавим показатели электровелосипеда. Также читайте обзор ТОПовых производителей велосипедов и не ошибайтесь с выбором.
Результаты:
- электровелосипед – 25-30 км/ч;
- шоссейный – 21-25 км/ч;
- туристический – 20-23 км/ч;
- гибрид – 19-21 км/ч;
- горный – 18-20 км/ч;
- городской – 15-17 км/ч.
Электровелосипед мог бы показать и больший результат, но его скорость езды ограничена контроллером. Для туристических велосипедов, оборудованных вело рюкзаками, оптимальной считается скорость 17 км/ч.
Город
Городские условия езды нивелируют скоростные характеристики разных типов велосипедов из-за необходимости частого маневрирования и преодоления препятствий. Скорость велосипеда в городе – 15-18 км/ч.

Так же интересен тот факт, что в условиях мегаполисов, на дистанциях до 5 км велосипед «быстрее» других видов транспорта. На дистанциях 5-10 км его средняя скорость сопоставима с автомобилем. Плюс у велосипедиста есть возможность двигаться не только по проезжей части, а проложить свой маршрут через парк или дворовые зоны.
Профессионалы
Опытные спортсмены способны преодолевать расстояния в 100 километров, двигаясь со средней скоростью около 30 км/ч. Так Руй Кошта (победитель групповой гонки на 242 км) в 2013 году проехал дистанцию со средней скоростью 36 км/ч.
Для примера приведем нормы получения разрядов велоспорт-шоссе в дисциплине «индивидуальная гонка на время» (РОССИЯ):
| Звание/разряд | Дистанция (км) | Время (минут) | Средняя скорость (км/ч) |
| МСМК мужчины | 50 | 64 | 46,88 |
| МСМК женщины | 25 | 35,5 | 42,25 |
| МС мужчины | 25 | 33 | 45,46 |
| МС женщины | 25 | 37,5 | 40 |
| КМС мужчины | 25 | 35,5 | 42,25 |
| КМС женщины | 25 | 40 | 37,5 |
Немного истории
По нормативам ГТО в СССР, чтобы получить золотой значок, необходимо было проехать на велосипеде:
| Возраст (лет)/пол | Дистанция (км) | Время (минут) | Средняя скорость (км/ч) |
| 19-28 мужчины | 20 | 43 | 27,91 |
| 18-28 женщины | 10 | 25 | 24 |
| 29-39 мужчины | 20 | 46 | 26,09 |
| 29-34 женщины | 10 | 27 | 22,22 |
Факторы, влияющие на скорость велосипеда
Подготовка велосипедиста
Больше всего скорость езды зависит от физической силы и выносливости человека. Второе место занимает техника езды. Пол ездока не оказывает существенного влияния на скорость передвижения.
Сопротивление воздуха
При отсутствии ветра, проблемы сопротивления воздушному потоку начинаются на скоростях в 25-27 км/ч. При встречном ветре трудности движения возникают при скорости 10-15 км/ч. Влияние воздушного потока зависит насколько правильная посадка велосипедиста.

На горном велосипеде, при высокой посадке, увеличивается площадь сопротивления набегающему потоку, и езда замедляется. На шоссейном велосипеде, благодаря узкому рулю с нижним захватом, есть возможность обеспечить туловищу практически горизонтальное положение. Это позволяет облегчить передвижение, благодаря уменьшению площади тела, сопротивляющемуся встречному потоку воздуха.
Сопротивление качению
На твердых поверхностях уменьшить сопротивление качению позволяет меньшая площадь соприкосновения колеса с дорожным полотном. Добиться этого можно, либо сильно накачав широкие покрышки, либо заменить их более узкими.

На мягких поверхностях (грунт или песок) все происходит наоборот. Широкие, или немного спущенные покрышки имеют приоритет перед узкими.
Размер колеса тоже имеет далеко не последнее значение. Велосипед с широкими колесами дольше сохраняет силу инерции и легче преодолевает неровности дорожного покрытия, что положительно сказывается на скорости езды.
Силы трения
На скорости велосипеда отражается техническое состояние его трущихся деталей. Цепь и втулки необходимо содержать в хорошо смазанном состоянии и не допускать их загрязнения. Слишком мягкие амортизаторы снижают скорость, но добавляют комфорта при движении по неровным поверхностям.
Надеемся, что информация данной статьи поможет вам оптимально выбрать и настроить велосипед под свои условия передвижения. Желаем вам хороших скоростей и удовольствия от езды.
Скорости движения на различных велосипедах в разных условиях

При поездке на велосипеде вокруг тебя нет железной коробки, как при езде на автомобиле, и ты открыт ветру и другим погодным условиям. При катании на велосипеде под тобой нет тяжелого стального корпуса, как при езде на мотоцикле, и ты просто летишь над землёй. Скорость в подобных условиях ощущается максимально полноценно.
Очень многие начинающие велосипедисты переоценивают скорость, с которой они ездят. Заметив на компьютере цифры 25-30 км/ч, многие думают, что с этой скоростью они чаще всего передвигаются, и это есть средняя скорость. Но это не так, такую скорость может удерживать только опытный велосипедист, а спортсмены кроме того способны на невообразимые рекорды.
Рекорды скоростей на велосипеде

Франческо Мозер
Максимальная скорость на велодроме – 51,151 км/ч. В гонке на треке в Мехико итальянский спортсмен Франческо Мозер в 1984 году за один час проехал расстояние 51,151 км. Такой результат считается рекордом скорости и выносливости. Как признался в 1999 году сам рекордсмен: удерживать высокую скорость и не сбивать темп ни на секунду ему помог кровяной допинг, который в то время был не запрещён.
Максимальная скорость по прямой, при установке на велосипед аэродинамического обтекателя – 133,78 км/ч. Этот мировой рекорд был поставлен 26 летним голландцем Себастьяном Боуйером в 2013 году на дистанции 200 метров. Спортсмен лежал на спине, у этого велосипеда педали установлены спереди, а сам веломобиль полностью закрыт сверхлегким обтекателем из углеродного волокна. Этот веломобиль был построен сообща студентами Свободного университета в Амстердаме и Дельфтского технологического университета.
Максимальная скорость по прямой, при укрытии велосипеда в воздушном мешке – 268,83 км/ч. Этот абсолютный рекорд скорости на велосипеде был поставлен 50-летним состоявшимся спортсменом Фредом Ромпельбергом из Нидерландов в 1995 году. Такой результат был достигнут на ровной поверхности высохшего соляного озера в штате Юта (Бонневилькая соляная равнина), и только благодаря следованию велосипеда за спереди движущимся гоночным автомобилем, большой обтекатель которого защищал велосипедиста от набегающего потока воздуха. Разумеется, был построен специальный велосипед, на котором невозможно ездить в обычных условиях.
Максимальная скорость при спуске с горы составляет 222 км/ч. Этот рекорд скорости установлен на маунтинбайке (горном велосипеде) французом Эриком Бароном в 2000 году на обкатанной ледяной горнолыжной трассе во Французских Альпах. Для установки этого предела скорости был построен велосипед с улучшенной аэродинамикой, но с амортизированной вилкой и задним подвесом. Сам спортсмен был одет в аэродинамический жёсткий костюм-скафандр. В 2002 году Эрик Барон, уже на сухом гравийном склоне вулкана Сьерра-Негро в Никарагуа смог разогнаться до 210,4 км/ч. Проехав около 400 метров велосипед под смельчаком, из-за невыносимой нагрузки на раму, разорвало на две части. Эрик Барон получил сильный перелом бедра, вывих левого плеча и шейного отдела позвоночника, многочисленные ушибы и порезы, но спортсмен выжил благодаря шлему и защитному костюму.
Максимальная средняя скорость на шоссейном велосипеде составляет 41,654 км/ч. Такую скорость смог держать на дистанции «Тур де Франс» американский шоссейный гонщик Лэнс Армстронг в 2005 году. На спусках с гор участники этого соревнования развивают скорость близкую к 90 км/ч.
Возможности неподготовленного велосипедиста
Труднодостижимые рекорды вдохновляют любого спортсмена, а обычному человеку, иногда выбирающемуся на велосипедные прогулки, намного интереснее узнать: с какой скоростью можно двигаться по обычным дорогам, не принимая участие в соревнованиях.
Для измерения скорости на велосипед, не так давно – пятнадцать-двадцать лет назад устанавливали большие, тяжелые и ненадежные механические спидометры. Сегодня каждый может позволить себе купить миниатюрный электронный велокомпьютер, который кроме текущей скорости и общего пробега отображает среднюю скорость движения, максимальную скорость, длину маршрута, темп в минуту, расход калорий, время в пути, и другу полезную информацию в более дорогих моделях.
Средний велосипедист на современном горном велосипеде без чрезмерных усилий может держать среднюю скорость 18-20 км/ч по шоссе, проезжая 10 км за 30 минут. Такой же велосипедист на шоссейном велосипеде может передвигаться со средней скоростью 20-25 км/ч по прямой асфальтированной дороге, проезжая 10 км за 25 минут. Пол ездока не имеет решающего значения, на таких скоростях. Средним велосипедистом считается человек, который катается примерно 20-50 часов в месяц или 1-2 часа в день.
На небольших расстояниях около 10 км развивать среднюю скорость 18 км/ч может каждый, включительно и подростки от 12-14 лет. Более опытный велосипедист, проезжающий не одну тысячу километров в год, аналогичную дистанцию проедет в два раза быстрее. У него выше физическая сила, лучше техника езды и, как правило, более качественный велосипед. Такие люди благодаря натренированной выносливости могут удерживать скорость около 30 км/ч, на дистанции 100 км по шоссе. На такие расстояния средний велосипедист крайне редко выезжает, или не ездит вовсе.
В городских условиях необходимо: объезжать остановившиеся автомобили и общественный транспорт, останавливаться на перекрестках и переездах, притормаживать до входа в повороты и перед пешеходами, поэтому средняя скорость велосипедиста в городе всегда ниже, чем на шоссе, приблизительно на 5-10 км/ч.

Несмотря на то, что на шоссейном велосипеде можно ездить быстрее по асфальту, чем на горном, его нельзя рекомендовать для поездок по городу. Байкер сидит низко на шоссейнике и имеет плохую обзорность, а остановится аварийно на таком велосипеде без заноса не получиться. Горный велосипед, хотя и медленнее шоссейного при движении по твердому покрытию, но более предпочтителен для езды по городу. На маунтингбайке очень легко маневрировать благодаря широкому рулю, а отличное сцепление широких шин с асфальтом позволит мгновенно застыть на месте.
При езде по пересеченной местности, даже на горном велосипеде, невозможно развить максимальную скорость 30 км/ч. Поскольку вне асфальта на пути часто встречаются ямы, бугры, песок, при проезде которых скорость значительно будет снижаться. При езде на маунтигбайке по лесной дороге средняя скорость обычно составляет 15 км/ч.
С другой стороны, шоссейный велосипед, имея малую толщину покрышек и большее распределение веса на переднее колесо, фактически не годится для катания по лесу. Средняя скорость движения шоссейного велосипеда при езде по песку, опавшим листьям, снегу составит 5-8 км/ч. При попытке преодолеть глубокий песок или снег на шоссейнике, переднее колесо занесет в сторону, или оно упрется в продавленный песок, и наездник, возможно, катапультируется через руль. Кроме того, при езде на велосипеде без амортизаторов по гравийной или прокатанной гусеничным транспортом дороге, очень быстро накапливается усталость, из-за ударов на руки и позвоночник.
Факторы, влияющие на скорость движения
Уровень подготовки велосипедиста
Скорость движения больше всего зависит от физической силы и выносливости наездника. Опыт ездока больше влияет на скорость езды, чем выбор типа велосипеда. При движении по шоссе опытный велосипедист на горном велосипеде сможет удержать на хвосте начинающих гонщиков на шоссейных велосипедах, сохраняя более высокую скорость даже при подъёмах в гору.
Сопротивление встречного воздуха
На скоростях 25-27 км/ч существенно тормозит движение велосипеда сопротивление воздуха. Если дует встречный ветер, то становится трудно двигаться уже на скорости 10-15 км/ч. На горном велосипеде с широким и высоко установленным рулём, а особенно, с низко опущенным седлом, намного тяжелее крутить педали на скорости 30 км/ч, чем на шоссейном велосипеде. У шоссейника имеется особенная деталь – узкий руль с нижним захватом (бараньи рога). При ощутимом сопротивлении встречного ветра наездник шоссейного велосипеда может пригнуться к рулю, захватив руль за нижнюю часть дуги, таким образом, значительно снизив нагрузку.

Полностью избавиться от давления встречного воздуха можно только заехав в воздушный мешок, под защитой впереди идущего автобуса или грузового автомобиля. Но пристраиваться сзади за автобус или грузовой автомобиль очень опасно, так как они могут резко затормозить или повернуть при объезде ямы.
Сопротивление качению
Особенно ощущается это противодействие в начале движения. На разгон с места из-за него уходит больше энергии, как у велосипедиста, так и у двигателя автомобиля. После начала движения сопротивление качению меньше сказывается на величине усилия, необходимого для разгона. С увеличением скорости движения это противодействие постепенно уменьшается.
Увеличение трения между шиной и дорогой в первую очередь повышает величину сопротивления качению. Узкую шину, которая продавила мягкий грунт тяжело оторвать от земли. Шина с широко расставленным протектором чрезмерно притирается к твердому асфальтному покрытию, к тому же при этом быстро стирается. Поэтому выбирать покрышки по ширине, площади и глубине протектора следует с учётом того, по каким дорогам вы будете ездить на велосипеде.
Давление в камере значительно влияет на трение между шиной и дорогой. Чем сильнее накачана камера, тем легче колесо катится по асфальту и твердому грунту. Для облегчения езды по щебню, песку, грязи, снегу давление в камерах рекомендуется снизить.
Большой вес велосипеда сильно повышает величину сопротивления качению. Разогнать и толкать в гору тяжелый горный велосипед всегда сложнее, чем более легкий шоссейный.
Увеличение диаметра колеса уменьшает величину сопротивления качению. Велосипед для взрослых значительно дольше двигается накатом по прямой, чем детский. Кроме того большое колесо легче преодолевает неровности дороги, перекатываясь через маленькие ямки.
Трение в передаточных механизмах
Скорость велосипеда наверняка снизит не смазанная или грязная цепь, а также изношенные втулки и каретка. Если вы стремитесь достичь большой скорости, тогда вам необходимо купить дорогие втулки и механизм каретки, и в дальнейшем следить за состоянием их смазки.
Амортизаторы на велосипеде, особенно слишком мягкие, снижают скорость по ровному асфальту. Но они оказываются незаменимыми при преодолении участков дорог с мелкими неровностями. Амортизированная вилка при движении по городу оказывается не заменимой, тогда как от заднего подвеса можно и отказаться.
Вообще то, сильно придерживаться приведенных выше средних скоростей не стоит, тем более максимальных. Вы должны кататься на велосипеде с удобной для вас скоростью, получая удовольствие от поездки.
Задачи на движение с примерами решения
2) скорость тела при движении по течению реки равна , а при движении против течения равна , где — собственная скорость тела (скорость в стоячей воде); — скорость течения реки; плот движется со скоростью течения реки.
При составлении уравнений в задачах на движение часто используются следующие очевидные утверждения:
1) если два тела, находящиеся перед началом движения на расстоянии , движутся навстречу друг другу со скоростями и , то время, через которое они встретятся, равно
2) если два тела, находящиеся перед началом движения на расстоянии , движутся в одном направлении со скоростями и , где , то время, через которое второе тело (его скорость ) догонит первое, равно .
Примеры с решениями
Пример №194.
Пешеход и велосипедист отправляются одновременно из пункта в пункт . В пункте велосипедист поворачивает обратно и встречает пешехода через 20 мин после начала движения. Не останавливаясь, велосипедист доезжает до пункта , поворачивает обратно и догоняет пешехода через 10 мин после первой встречи. За какое время пешеход пройдет путь от до ?
Решение:
Пусть и — скорости (в километрах в час) соответственно пешехода и велосипедиста, — путь (в километрах) . Так как пешеход и велосипедист встретились через ч, пройдя вдвоем путь , то
За полчаса, истекших от начала движения до того момента, когда велосипедист догнал пешехода, разность пройденных ими расстояний была равна , т. е.
Запишем систему уравнений (1), (2) в виде f Vi + vo = 6s,
и вычтем из первого уравнения системы (3) второе. Получим , откуда найдем искомую величину
Пример №195.
Пристань находится выше по течению реки, чем пристань . Из и одновременно навстречу друг другу начали движение плот и моторная лодка. Достигнув пристани , моторная лодка немедленно повернула обратно и догнала плот в тот момент, когда он проплыл расстояния между и .
Найти время, которое затрачивает плот на путь из в , если моторная лодка проплывает из в и обратно за Зч.
Решение:
Пусть — расстояние между пунктами и , и — скорость течения реки, — скорость моторной лодки в стоячей воде. Тогда

Полагая запишем систему (4) в виде

Первое из уравнений системы (5) приводится к однородному уравнению откуда Подставив это выражение во второе уравнение системы (5), получаем откуда
Пример №196.
Из пункта в пункт вышел пешеход. Вслед за ним через 2 ч из пункта выехал велосипедист, а еще через 30 мин — мотоциклист. Все участники движения перемещались равномерно и без остановок.
Через некоторое время после выезда мотоциклиста оказалось, что все трое преодолели одинаковую часть пути от до . На сколько минут раньше пешехода прибыл в пункт велосипедист, если пешеход прибыл туда на 1 ч позже мотоциклиста?
Решение:
Первый способ. Пусть — точка на пути , в которой одновременно оказались участники движения, , ; , , — скорости пешехода, велосипедиста и мотоциклиста соответственно, — искомое время. Используя условия задачи, составляем систему уравнений

Далее, из (6) получаем
и следовательно ,

Второй способ. Рассмотрим координатную плоскость, по оси абсцисс будем откладывать время , а по оси ординат — пройденный путь (рис. 17.1).
Пусть отрезки — графики движения пешехода, велосипедиста и мотоциклиста соответственно. По условию эти отрезки имеют общую точку с ординатой , точки лежат на прямой где — искомое время.
Так как то откуда
Пример №197.
Автомобилист и велосипедист, выехавшие одновременно соответственно из пунктов и , совершают безостановочное движение между этими пунктами. Доехав до пункта и повернув назад, автомобилист догнал велосипедиста через ч. после их первой встречи. Сколько времени после первой встречи ехал велосипедист до пункта , если к тому моменту, когда его обогнал автомобилист, он проехал пути от до ?
Решение:
Первый способ. Пусть — расстояние между пунктами и , и — скорости автомобиля и велосипедиста соответственно, — время (в часах) от начала движения до первой встречи. Тогда

Требуется найти величину Разделив почленно уравнения (10) и (9), получим
Из (8) и (11) следует, что
Наконец, из равенств (12) и (13) получаем и
Следовательно,
Ответ. 8 ч 45 мин.
Второй способ. Решим задачу, не составляя систему уравнений. От начала движения до того момента, когда автомобилист обогнал велосипедиста, они проехали и — пути от до . Поэтому отношение их скоростей равно
Следовательно, к моменту первой встречи участники движения проехали и пути от до . Но, затратив на дорогу еще ч, велосипедист проезжает всего пути. Значит, за 1ч он проезжает пути. Оставшуюся после первой встречи часть пути велосипедист проедет за
Пример №198.
Дорога проходит через пункты и . Велосипедист выехал из по направлению к . Одновременно с ним из пункта вышли с равными скоростями два пешехода: первый — в пункт , а второй — в противоположном направлении. Велосипедист проехал от до за 0,5ч и, продолжая движение, догнал второго пешехода. Это произошло через 1,2 ч после встречи велосипедиста с первым пешеходом. Определить время движения велосипедиста от начала движения до встречи с первым пешеходом.
Решение:
Пусть — место встречи велосипедиста с первым пешеходом (рис. 17.2).

Пусть — скорость велосипедиста, — скорость каждого из пешеходов. Тогда искомое время
Согласно условию задачи имеем
где — место (пункт), где велосипедист догнал второго пешехода, вышедшего из (в направлении ). Так как велосипедист и первый пешеход вышли одновременно, то время, в течение которого они находились в пути до встречи в , составляет
Расстояние велосипедист преодолел за ч, а второй пешеход за это время прошел км со скоростью . Следовательно,
Уравнение (16) в силу (14) и (15) можно записать так:
Аналогично, используя равенства (14) и (15), преобразуем уравнение (17):
Из (18) и (19) следует, что
откуда
Пример №199.
Из пунктов и навстречу друг другу вышли одновременно два поезда. Каждый из них двигался сначала равноускоренно (начальные скорости поездов равны нулю, ускорения различны), а затем, достигнув некоторой скорости, — равномерно. Отношение скоростей равномерного движения поездов равно . В момент встречи поезда имели равные скорости, а в пункты и прибыли одновременно. Найти отношение ускорений поездов.

Решение:
Пусть и — скорости равномерного движения первого и второго поездов, и — их ускорения. Предположим, что , тогда
Графики скоростей поездов как функций времени изображены на рис. 17.3.
Здесь и — время равноускоренного движения поездов, — момент их встречи, — время прохождения пути каждым из поездов. Заметим, что а так как и в момент поезда имели равные скорости.
Из равенств и условия (20) следует, что
Таким образом, для решения задачи нужно найти отношение
По условию в момент поезда имели равные скорости. Следовательно,
Из (22) и (20) находим
Пусть — все расстояние, пройденное каждым из поездов, тогда величина равна площади каждой из трапеций и (рис. 17.3), т. е.
Из равенств (24), (25) и (20) находим
Итак, получены уравнения (23) и (26), связывающие и . Не хватает еще одного уравнения. Такое уравнение (и в этом ключ к решению задачи) мы получим, заметив, что сумма расстояний и , пройденных поездами до встречи, равна .
![]()
Из (24), (27) и (23) следует, что т.е.
а из (26) и (28) получаем
Наконец, из равенств (21) и (29) находим, что
Ответ.
Пример №200.
Два велосипедиста движутся по кольцевой велотрассе длины , часть которой проходит по стадиону, а оставшаяся часть — по городским улицам. Скорость первого велосипедиста на стадионе равна , а на городских улицах равна . Скорость второго велосипедиста на стадионе равна , а на городских улицах . Велосипедисты одновременно въезжают на стадион. Через какое время после этого один из них впервые совершит обгон другого?
Решение:
Первый велосипедист проезжает полный круг за время

а второй — за время
Поэтому второй велосипедист догонит первого, если проедет на круг больше, чем первый, причем это произойдет на стадионе, поскольку там скорость второго больше, чем у первого.
Пусть — время от начала движения до момента, когда второй совершит обгон первого; — число целых кругов, пройденных до обгона вторым велосипедистом; — часть пути по стадиону, пройденная велосипедистами после кругов, пройденных вторым.
Так как на полный круг первый затрачивает на больше, чем второй, то второй, отрываясь от первого, догонит первого, когда выигрыша во времени будет достаточно, чтобы второй проехал круг. Поэтому второму достаточно проехать полных кругов чтобы затем на стадионе обогнать первого. Из условия равенства времени движения каждого его участника с учетом пройденного пути получаем систему уравнений

откуда (при ) находим

Ответ.
Пример №201.
Катер по реке и автобус по дороге, идущей вдоль берега реки, отправляются одновременно из пункта А в пункт В и совершают безостановочное движение между А и В. Первая их встреча произошла, когда автобус прошел — всего расстояния от А до В, а вторая встреча — когда автобус после первого захода в В проехал всего расстояния от В до А. Первый раз в пункт В автобус прибыл на 16 мин позже катера. Через сколько часов после начала движения автобус и катер окажутся одновременно в пункте А, если скорость катера в неподвижной воде и скорость автобуса постоянны ?
Решение:
Первый способ. Пусть и — время (в часах), за которое проходят путь АВ автобус и катер соответственно, a время, за которое катер проходит путь ВА, — расстояние АВ.
До первой встречи в пункте С автобус прошел путь за время . Такое же время катер затратил на АВ и путь ВС, равный . Следовательно,
До второй встречи автобус затратил время а катер — время (на АВ), затем (на ВА) и еще — . Значит,
По условию, автобус первый раз прибыл в В на 16 мин (на ч) позже катера, т. е.
Решив систему (30)-(32) находим
Автобус оказывается в пункте А, преодолев (четное число раз) путь от А до В и затратив время . Катер окажется в пункте А, совершив рейсов от А до В и рейсов от В до А и затратив время Одновременно в пункте А автобус и катер окажутся лишь в том случае, когда найдутся и такие, что т. е.
Так как 12 и 5 — взаимно простые числа, то число является целым только в том случае, когда делится на 5. Наименьшее возможное число и тогда
Итак, автобус и катер первый раз одновременно окажутся в пункте А, если автобус сделает рейсов (катер—12) и затратит время
Ответ. Через 4 ч.
Второй способ. Пусть — скорости соответственно катера в стоячей воде, автобуса и течения реки, — расстояние от А до В (река течет от А к В, скорость — в километрах в минуту). Тогда, учитывая, что до первой и второй встречи катер и автобус затратили одинаковое время, получаем

Так как катер пришел в пункт В на 16 мин раньше автобуса, то
Введем следующие обозначения:
Тогда система (33)—(35) примет вид

Линейная система (36) имеет решение Время, затраченное катером на путь от А до В и обратно, равно (мин), а время, затраченное автобусом на тот же путь, равно Одновременно автобус и катер первый раз окажутся в пункте А через целое число поездок, поэтому искомое время есть наименьшее общее кратное чисел 48 и 20 и равно 240 мин, т. е. 4 ч.
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Двухколёсный галоп: какую скорость можно развить на велосипеде?

Скорость велосипеда — величина неоднозначная. Как и в случае с автомобилем, она зависит от условий местности, типа велосипеда и навыков самого велосипедиста. Поэтому, говоря о средней скорости, трудно с абсолютной уверенностью определить конкретное число. Но вот выяснить, сколько примерно километров можно преодолеть в час в условиях города или трассы, пользуясь тем или иным типом железного коня, можно без особого труда.
Средняя скорость в зависимости от местности
Обычно выделяют три типа местности, наиболее актуальных для велосипедиста:
- город или населённый пункт городского типа
- трасса
- пересечённая местность
Разумеется, развить высокую скорость в городе сложно: много участников дорожного движения. Велосипедисту обычно остаётся передвигаться по дорогам, прижимаясь к правой их стороне, в общем потоке машин. Приходится быть вдвойне осторожным, чтобы случайно не попасть под колёса.

Средняя скорость зависит и от того, насколько часто встречаются на пути перекрёстки со светофорами, а также от степени загруженности дорог. Пробки велосипедисту не страшны, зато часто возникает необходимость лавировать среди автомобилей. А вот в небольших городах с не очень плотным дорожным движением разогнаться уже проще.
В зависимости от всех этих условий средняя скорость велосипедиста в городских условиях составляет от 10 до 15-17 км/ч. Если же город может похвастаться наличием велосипедных дорожек, то она увеличивается до 15-17 км/ч. При условии, конечно, что те используются по назначению, и по ним не передвигаются пешеходы.
На шоссе средняя скорость возрастает благодаря отсутствию светофоров и пешеходных переходов. Зависит она от качества дорожного покрытия и типа велосипеда. На небольших, специально предназначенных для города моделях вряд ли получится превысить отметку в 20 км/ч. А вот если брать в расчёт обычные универсальные велосипеды, то можно говорить о средней скорости 20-25 км/ч. На шоссейных же можно разогнаться до 28-32 км/ч, но поддерживать более высокую скорость под силу только опытным велосипедистам с отличной физической подготовкой.
Понятие “пересечённая местность” имеет довольно абстрактный характер. Оно может включать в себя и достаточно удобное для езды бездорожье, и изобилующие оврагами долины. Поэтому и разница между минимальным и максимальным пределами скорости велика: от 5 до 15 км/ч.
Средняя скорость в зависимости от типа велосипеда

осмотрим, на какую скорость можно рассчитывать в среднем, используя разные типы велосипедов.
- дорожные велосипеды. Эти модели наиболее просты: большие, довольно тяжёлые, как правило, не предусматривающие переключение скоростей. Предназначены они в основном для передвижения по городу и шоссе с хорошим покрытием. Скорость их невелика: не стоит рассчитывать превысить отметку в 13-15 км/ч даже на прекрасной ровной поверхности
- городские велосипеды. Их ещё часто называют прогулочными. Они уже гораздо более функциональны по сравнению с дорожными. Небольшой вес, удобная, функциональная конструкция и возможность переключения скоростей обеспечивают среднюю скорость в пределах 12-17 км/ч в городе и около 20 км/ч на трассе
- на шоссейных велосипедах несложно развить и поддерживать среднюю скорость в 28-33 км/ч
- MTB велосипеды (горные). Если ездить на горном байке по шоссе, обычно можно выйти на среднюю скорость в 25 км/ч. Если сменить покрышки на предназначенные для езды по асфальту, скорость увеличивается на 3-4 км/ч. В условиях пересечённой местности скорость, как правило, составляет от 10 до 15 км/ч
- гибрид. Этот велосипед представляет собой нечто промежуточное между шоссейным и горным типами байков. Скорость на трассе — около 25-28 км/ч, по бездорожью — около 10 км/ч
Рекорды скорости
Абсолютный рекорд скорости был поставлен спортсменом Фредом Ромпелбергом в 1995 году. На своём спортивном велосипеде он достиг отметки в 268 км/ч.
К другим рекордным результатам можно отнести достижения спортсменов первой половины 20 века: например, в 1937 году один из них развил скорость в 139 км/ч, а другой в 1942 году побил этот рекорд, разогнавшись до 175 км/ч.
Подводя итоги
Говорить о средней скорости велосипеда можно только с оговорками. Помимо вида местности и типа байка, на скорость влияет множество факторов. Это и уровень физической подготовки велосипедиста, и множество технических деталей: например, диаметр и масса колёс, геометрические особенности конструкции, сопротивление воздуха и т.д. Есть лишь примерное представление о том, какую среднюю скорость удастся поддерживать в городе или на трассе, на горном байке или обычном городском велосипеде.
Задачи на движение
Задачи на движение начинают проходить в 5 классе и решают все оставшиеся учебные годы вплоть до 11 класса. В ЕГЭ по математике вы найдете задачи на движение в задании 11, в котором собраны все текстовые задачи. Рассмотрим как надо решать задачи на движение из ЕГЭ. Но сначала немного теории.
Как решать задачи на движение
Решение задач на движение подчиняется четкому алгоритму, который состоит из нескольких этапов:
- Анализ данных.
- Составление таблицы.
- Составление уравнения.
- Решение уравнения.
Остановимся подробно на каждом пункте:
1. Первое, с чего нужно начать — медленно и вдумчиво прочитать условие задачи, то есть проанализировать данные.
Чтобы наглядно представить задачу, необходимо сделать рисунок и отобразить на нем все известные по условию задачи величины.
2. Второй шаг — составить таблицу по условию задачи, внести в таблицу известные величины и ввести неизвестные.
Таблица состоит из трех столбцов S, v и t (путь, скорость и время) и нескольких строк. При заполнении каждой строки сначала выбираем и заполняем тот столбец, информация о котором дана в задаче. Еще один столбец записываем в роли неизвестного (чаще всего, это то, что требуется найти в задаче). В третью, оставшуюся колонку вписываем связь характеристик из двух уже заполненных столбцов по формуле:
В таблице получается столько строчек, сколько каждый из объектов задачи действовал (то есть, перемещался) или мог бы действовать.
3. Следующий шаг — при помощи сделанного рисунка и заполненной таблицы составить уравнение или систему уравнений.
По окончании заполнения таблицы оказывается, что есть часть информации, которая не вошла в таблицу. Эта информация характеризует те значения величин в колонках, которые вычисляются в третью очередь, то есть по формуле. На основании этой информации и данных из третьей колонки составляем уравнение.
4. Решить полученное уравнение и прийти к ответу.
Когда уравнение составлено, последний шаг — это решить его, и, в конце концов, получить ответ.
Будьте внимательны, если за неизвестное вы приняли не то, что требуется найти в задаче. В этом случае следует выразить то, что нужно найти через полученное решение уравнения.
Если, решив уравнение, вы получили несколько ответов, то следует отобрать только имеющие смысл решения. Помните, что путь, скорость и время не могут быть отрицательными.
Примеры решения
Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.
В задаче требуется найти скорость второго, более медленного, велосипедиста. Примем его скорость за x. Заполним таблицу:
| v, км/ч | t, ч | S, км | |
| Первый велосипедист | x + 10 | 60 | |
| Второй велосипедист | x | 60 |
В условии задачи сказано, что первый велосипедист прибыл к финишу на 3 часа раньше второго. На основании этого составим уравнение:
Получаем два корня, x1 = 10 и x2 = –20. Второй корень не подходит, так как скорость не может быть отрицательной.
Виды задач на движение
Если два объекта движутся навстречу друг другу, то они сближаются:
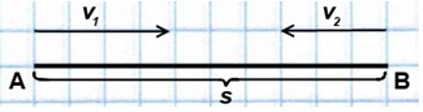
При движении в противоположном направлении объекты удаляются:
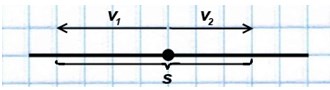
В обоих случаях объекты как бы «помогают» друг другу преодолеть общее для них расстояние, «действуют сообща». Поэтому чтобы найти их совместную скорость (это и будет скорость сближения или удаления), нужно складывать скорости объектов:
Движение друг за другом (вдогонку)
При движении в одном направлении объекты также могут как сближаться, так и удаляться. В этом случае они как бы «соревнуются» в преодолении общего расстояния, «действуют друг против друга». Поэтому их совместная скорость будет равна разности скоростей.
Если скорость идущего впереди объекта меньше скорости объекта, следующего за ним, то они сближаются. Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:
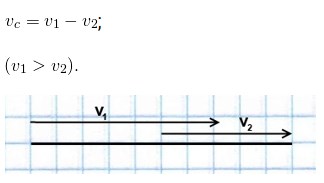
Если объект, идущий впереди, движется с большей скоростью, чем идущий следом за ним, то они удаляются. Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:
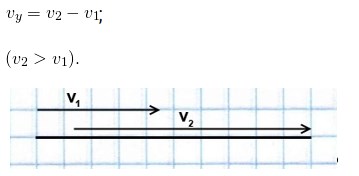
При движении навстречу друг другу и движении в противоположных направлениях скорости складываем.
При движении в одном направлении скорости вычитаем.
Задачи на движение по кругу
При движении по кругу объекты могут:
- сближаться, если скорость догоняющего больше скорости догоняемого. Скорость сближения будет равна ;
- отдаляться, если скорость догоняющего меньше скорости догоняемого. Скорость удаления будет равна .
При этом пройденные расстояния измеряются длиной круговой трассы, равной S.
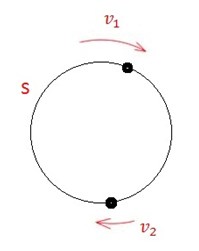
- Если два объекта начинают движение по кругу из одной и той же точки, то в момент первой встречи более быстрый объект пройдет расстояние на один круг больше.
- Если два объекта начинают движение по кругу из разных точек, расстояние между которыми равно S0, то в момент первой встречи догоняющий объект пройдет на S0 км большее расстояние, чем догоняемый.
- Если через определенное время t первый объект опережает второй на m кругов, то разница пройденных объектами расстояний будет равна m · S: S1 – S2 = m · S.
Задачи на движение мимо объекта
В задачах на движение мимо объекта обязательно присутствуют протяженные тела — поезда, туннели, корабли и т. п. Зачастую движущимся объектом является поезд.
Если поезд длиной L движется мимо точечного объекта (столба, светофора, человека), то он проходит расстояние, равное его длине L:
При этом, если точечный объект (пешеход, велосипедист) тоже движется, то совместная скорость равна сумме скоростей, если поезд и объект двигаются в разных направлениях (как в пункте 1), и равна разности скоростей, если они двигаются в одном направлении (как в пункте 2).
Если поезд длиной L1 движется мимо протяженного объекта (туннеля, лесополосы) длиной L2, то он проходит расстояние, равное сумме длин самого поезда и протяженного объекта:
S = L1 + L2 = v0 · t.
При этом, если протяженный объект (например, другой поезд) тоже движется, то совместная скорость равна сумме скоростей, если оба объекта двигаются в разных направлениях, и равна разности скоростей (из большей вычитается меньшая), если они двигаются в одном направлении.
Задачи на движение по течению и против течения
В задачах на движение помимо собственной скорости плывущего тела нужно учитывать скорость течения.
При движении по течению скорость течения прибавляется к скорости плывущего тела: v = v0 + vтеч.
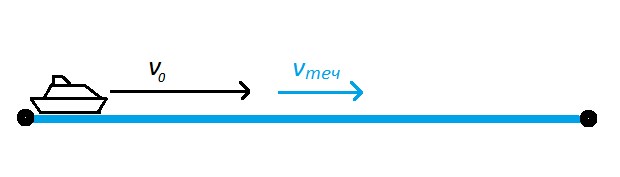
При движении против течения скорость течения отнимается от скорости плывущего тела: v = v0 – vтеч.

Задачи на движение из ЕГЭ по математике (профильный уровень)
Задача 1.
Из одной точки круговой трассы, длина которой равна 44 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 112 км/ч, и через 48 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение: Пусть скорость второго автомобиля равна v км/ч. За 4/5 часа первый автомобиль прошел на 44 км больше, чем второй, отсюда имеем:
112 ∙ alt=»\frac{4}{5}» width=»7″ height=»22″ />= v ∙ alt=»\frac{4}{5}» width=»7″ height=»22″ />+ 44 ⇔ 4 ∙ v = 112 ∙ 4 – 44 ∙ 5 ⇔ v = 57.
Следовательно, скорость второго автомобиля была равна 57 км/ч.
Ответ: 57 км/ч.
Задача 2.
Из пункта A круговой трассы выехал велосипедист, а через 10 минут следом за ним отправился мотоциклист. Через 2 минуты после отправления он догнал велосипедиста в первый раз, а еще через 3 минуты после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 5 км. Ответ дайте в км/ч.
Решение:
До первой встречи велосипедист провел на трассе 1/5 часа, а мотоциклист 1/30 часа. Пусть скорость мотоциклиста равна v км/ч, тогда скорость велосипедиста равна
Тогда если скорость велосипедиста – это 1 единица отношения, то скорость мотоциклиста – это 6 единиц отношения.
Так как они едут в одном направлении, их общая скорость 5 единиц отношения.
∙5 ед.отн. = 5
Таким образом, скорость мотоциклиста была равна 120 км/ч.
Ответ: 120 км/ч.
Задача 3
Часы со стрелками показывают 3 часа ровно. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?
Решение: Скорость движения минутной стрелки 12 делений/час (под одним делением здесь подразумевается расстояние между соседними цифрами на циферблате часов), а часовой ― 1 деление/час. До девятой встречи минутной и часовой стрелок минутная должна сначала 8 раз «обогнать» часовую, то есть пройти 8 кругов по 12 делений. Пусть после этого до четвертой встречи часовая стрелка пройдет L делений. Тогда общий путь минутной стрелки складывается из найденных 96 делений, ещё 3 изначально разделяющих их делений (поскольку часы показывают 3 часа) и последних L делений. Приравняем время движения для часовой и минутной стрелок:
, отсюда и .
Ответ: через 9 минут.
Задача 4
Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение:
Данную задачу можно интерпретировать (представить её, как задачу на линейное движение): Два автомобиля одновременно начинают движение в одном направлении. Скорость первого равна 80 км/ч. Через 40 минут он опережает второго на 14 км (т. к. сказано, что на один круг). Найти скорость второго. Очень важно в заданиях на движение представить сам процесс этого движения.
Сравнение так же производим по расстоянию.
За x принимаем искомую величину ― скорость второго. Время движения 40 минут (2/3 часа) для обоих. Заполним графу «расстояние»:
| v | t | S | |
| 1 | 80 | 2/3 | |
| 2 | x | 2/3 |
Расстояние, пройденное первым, больше расстояния, который прошёл второй на 14 км.
80 ∙ alt=»\frac{2}{3}» width=»7″ height=»22″ />больше, чем x ∙ alt=»\frac{2}{3}» width=»7″ height=»22″ />на 14.
80 ∙ alt=»\frac{2}{3}» width=»7″ height=»22″ />= x ∙ alt=»\frac{2}{3}» width=»7″ height=»22″ />+ 14;
– = x ∙ ;
Скорость второго автомобиля 59 (км/ч).
Ответ: 59 км/ч.
Задача 5
Из пункта A в пункт B, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 6 часов позже автомобилиста. Ответ дайте в км/ч.
Решение:
Пусть v км/ч – скорость велосипедиста, тогда скорость автомобилиста равна v + 40 км/ч. Велосипедист был в пути на 6 часов больше, отсюда имеем:
Источники:
https://zextrem.com/zemlya/velosport/srednyaya-skorost-velosipeda.html
https://velofans.ru/skorosti-dvizheniya-razlichnyh-velosipedah-raznyh-usloviyah
https://9219603113.com/zadachi-na-dvizhenie-s-primerami-resheniya/
https://sport-51.ru/article/cycle-racing/9189-dvuhkolesnyj-galop-kakuju-skorost-mozhno-razvit-na-velosipede.html
https://novstudent.ru/zadachi-na-dvizhenie/
