Как ездить по оживленному шоссе на велосипеде

Изначально, большинство велосипедистов передвигаются по паркам и скверам. Хорошо, если в районе, недалеко от дома, есть велодорожка. Но рано или поздно каждый желает воспользоваться велосипедом не как развлечением, а как транспортным средством, способным доставить его в пункт назначения. И перед тем, как выехать на оживленную улицу или автостраду, нужно изучить правила езды на велосипеде по шоссе и городу.
Перед выездом
Сначала необходимо убедиться в исправности транспортного средства. Это связано не только с неприятностями, которые могут настичь:
- ремонт под открытым небом;
- потеря времени;
- необходимость транспортировать его в руках или на машине и т.д.
Все кроется в обеспечении безопасности собственного здоровья и жизни. Падение теперь грозит не просто ушибами, а возможностью попасть под машину. Поэтому, перед тем, как начать движение на велосипеде по трассе или городским магистралям, нужно убедиться, что исправны следующие узлы:
- колеса достаточно накачаны и не спускают; эффективны и функционируют нормально;
- габаритные огни горят;
- на цепи нет грязи и видимых повреждений.
Крайне желательно проверить все винтовые крепления. Это не займет много времени, но может спасти жизнь.
Разрешена ли езда по тротуарам вдоль оживленных улиц?
Многие боятся ездить на велосипеде по трассе или дорогам с оживленным автомобильным трафиком. При этом принимается решение съехать на тротуар и передвигаться по нему. Правила движения рассматривают велосипед как полноценное транспортное средство, и поэтому такое перемещение запрещается. Однако есть льготные категории лиц, на которых данный запрет не распространяется:
- . Имеются в виду лица, не достигшие четырнадцатилетнего возраста. И то, это можно делать под присмотром взрослых сопровождающих.
- Совершеннолетним лицам, транспортирующих детей, возраст которых не достиг семи лет.

Если навыков езды по дорогам недостаточно, и страх вас не отпускает, и вы все-таки выехали на пешеходную дорожку, нужно придерживаться следующих рекомендаций:
- Не сигнальте прохожим.
- Придерживайтесь края тротуара ближе к дороге.
- Встаньте и пройдитесь пешком, если на пути много людей. При малейшем сомнении исключите риск столкновения полностью.
- Всегда ожидайте непредсказуемого поведения, особенно если на пути или рядом с траекторией находятся дети.
- Уважительно относитесь к мамам с колясками. В этой ситуации они правы на 100%.
Данные рекомендации не являются разрешением для езды по тротуарам, а лишь нацелены на элементарную вежливость и безопасность прохожих. Факт нарушения присутствует, и никуда от него не деться.
Правила езды по оживленным улицам, шоссе и трассам
Разрешается езда на велосипеде по шоссе и дорогам общего пользования лицам, старше 14-и лет. Краткий, но достаточный перечень правил, которые необходимо заучить как «дважды два», следующий:
- Двигайтесь вместе с потоком.
- Заблаговременно оповещайте ручными сигналами других участников движения о своих маневрах.
- Изучите ПДД и неукоснительно их соблюдайте в отношении показаний светофоров и указаний дорожных знаков и разметки.
- Сбрасывайте скорость при везде на перекресток или со второстепенной дороги (со двора, в том числе).
- Всегда помните о правиле правой руки. Если перекресток нерегулируемый, вы обязаны пропустить транспорт, движущийся на вас справа.
- Пересекать дорогу по «зебре» можно только встав с велосипеда.
- Позаботьтесь, чтобы спереди горел белый габаритный огонь, а сзади – красный. Они должны быть исправны всегда.

Наезжая на бордюр, лежачий полицейский или иное небольшое препятствие, сбрасывайте скорость и продолжайте движение перпендикулярно препятствия. Это исключит падение по причине скольжения колеса. А чтобы не стать заложником собственных эмоций, воспользуйтесь следующими советами:
- не встревайте в конфликты с водителями и пешеходами;
- сохраняйте спокойствие;
- пропускайте пешеходов на пешеходных переходах;
- сбрасывайте скорость, если видите, что некто собирается перебежать дорогу перед вами.
Это общие правила, касающиеся движения на велосипеде по трассе или городским улицам. Сюда же можно добавить и требования к одежде.
Нужна ли экипировка?
К специальной одежде, необходимой на дорогах и трассах относится:
- шлем;
- перчатки;
- комплект верхней одежды;
- специальная обувь.
У многих все это отсутствует, и напрасно. И если к обуви есть немного требований (должна «дышать» и быть удобной), то к одежде их больше.
Движение на велосипеде – физическая нагрузка, за что мы его и любим. Но летом, это еще и повышенная температура. И если хорошенько пропотеть, то можно заболеть. А если одеться слишком тепло, может случиться тепловой удар, а потерять сознание на велосипеде во время езды по трассе чревато непоправимым исходом.
Шлем – основная защита велосипедиста при езде на велосипеде по шоссе и городским улицам, и пренебрегать ин ни в коем случае нельзя. Голова у нас одна, и не защитить ее мы не имеем права. Чтобы правильно подобрать шлем, воспользуйтесь нашими рекомендациями.
И конечно, перчатки. Все велосипедисты делятся на тех, кто падал, и тех, у кого падения еще впереди. Ладони первыми принимают удар. Перчатки уберегут от повреждений кожный покров, а суставы, фаланги пальцев и кисть от переломов, вывихов и ушибов.
А чтобы ваш организм не был обезвожен, возьмите с собой бутылку воды. Пейте небольшими глотками во время остановок.

Чтобы ездить на велосипеде по трассе, пользуйтесь правилами:
- Едем по направлению движения транспорта.
- При необходимости совершить поворот влево лучше съехать на обочину и перейти шоссе пешком.
- Не останавливайтесь в местах, где установлены отбойники. Выбирайте место, где ширина обочины позволяет съехать с проезжей части на безопасное расстояние.
- Управляйте двумя руками. Не разговаривайте по телефону без гарнитуры, а лучше вообще не разговаривайте. Не пейте воду на ходу.
Придерживаться этих несложных правил означает сохранить себе жизнь и здоровье и многие годы наслаждаться велосипедными прогулками.
Задачи на движение
Задачи на движение начинают проходить в 5 классе и решают все оставшиеся учебные годы вплоть до 11 класса. В ЕГЭ по математике вы найдете задачи на движение в задании 11, в котором собраны все текстовые задачи. Рассмотрим как надо решать задачи на движение из ЕГЭ. Но сначала немного теории.
Как решать задачи на движение
Решение задач на движение подчиняется четкому алгоритму, который состоит из нескольких этапов:
- Анализ данных.
- Составление таблицы.
- Составление уравнения.
- Решение уравнения.
Остановимся подробно на каждом пункте:
1. Первое, с чего нужно начать — медленно и вдумчиво прочитать условие задачи, то есть проанализировать данные.
Чтобы наглядно представить задачу, необходимо сделать рисунок и отобразить на нем все известные по условию задачи величины.
2. Второй шаг — составить таблицу по условию задачи, внести в таблицу известные величины и ввести неизвестные.
Таблица состоит из трех столбцов S, v и t (путь, скорость и время) и нескольких строк. При заполнении каждой строки сначала выбираем и заполняем тот столбец, информация о котором дана в задаче. Еще один столбец записываем в роли неизвестного (чаще всего, это то, что требуется найти в задаче). В третью, оставшуюся колонку вписываем связь характеристик из двух уже заполненных столбцов по формуле:
В таблице получается столько строчек, сколько каждый из объектов задачи действовал (то есть, перемещался) или мог бы действовать.
3. Следующий шаг — при помощи сделанного рисунка и заполненной таблицы составить уравнение или систему уравнений.
По окончании заполнения таблицы оказывается, что есть часть информации, которая не вошла в таблицу. Эта информация характеризует те значения величин в колонках, которые вычисляются в третью очередь, то есть по формуле. На основании этой информации и данных из третьей колонки составляем уравнение.
4. Решить полученное уравнение и прийти к ответу.
Когда уравнение составлено, последний шаг — это решить его, и, в конце концов, получить ответ.
Будьте внимательны, если за неизвестное вы приняли не то, что требуется найти в задаче. В этом случае следует выразить то, что нужно найти через полученное решение уравнения.
Если, решив уравнение, вы получили несколько ответов, то следует отобрать только имеющие смысл решения. Помните, что путь, скорость и время не могут быть отрицательными.
Примеры решения
Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.
В задаче требуется найти скорость второго, более медленного, велосипедиста. Примем его скорость за x. Заполним таблицу:
| v, км/ч | t, ч | S, км | |
| Первый велосипедист | x + 10 | 60 | |
| Второй велосипедист | x | 60 |
В условии задачи сказано, что первый велосипедист прибыл к финишу на 3 часа раньше второго. На основании этого составим уравнение:
Получаем два корня, x1 = 10 и x2 = –20. Второй корень не подходит, так как скорость не может быть отрицательной.
Виды задач на движение
Если два объекта движутся навстречу друг другу, то они сближаются:
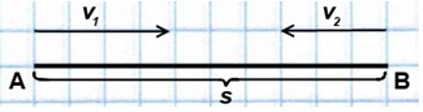
При движении в противоположном направлении объекты удаляются:
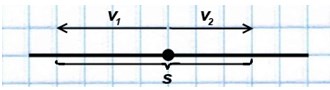
В обоих случаях объекты как бы «помогают» друг другу преодолеть общее для них расстояние, «действуют сообща». Поэтому чтобы найти их совместную скорость (это и будет скорость сближения или удаления), нужно складывать скорости объектов:
Движение друг за другом (вдогонку)
При движении в одном направлении объекты также могут как сближаться, так и удаляться. В этом случае они как бы «соревнуются» в преодолении общего расстояния, «действуют друг против друга». Поэтому их совместная скорость будет равна разности скоростей.
Если скорость идущего впереди объекта меньше скорости объекта, следующего за ним, то они сближаются. Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:
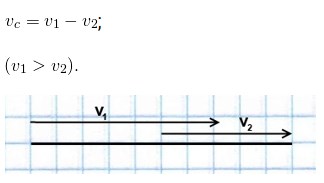
Если объект, идущий впереди, движется с большей скоростью, чем идущий следом за ним, то они удаляются. Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:
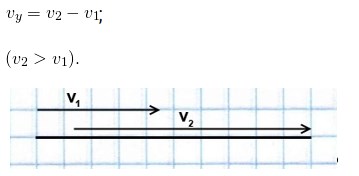
При движении навстречу друг другу и движении в противоположных направлениях скорости складываем.
При движении в одном направлении скорости вычитаем.
Задачи на движение по кругу
При движении по кругу объекты могут:
- сближаться, если скорость догоняющего больше скорости догоняемого. Скорость сближения будет равна ;
- отдаляться, если скорость догоняющего меньше скорости догоняемого. Скорость удаления будет равна .
При этом пройденные расстояния измеряются длиной круговой трассы, равной S.
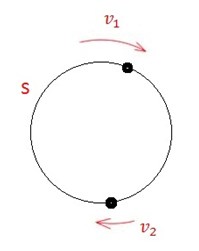
- Если два объекта начинают движение по кругу из одной и той же точки, то в момент первой встречи более быстрый объект пройдет расстояние на один круг больше.
- Если два объекта начинают движение по кругу из разных точек, расстояние между которыми равно S0, то в момент первой встречи догоняющий объект пройдет на S0 км большее расстояние, чем догоняемый.
- Если через определенное время t первый объект опережает второй на m кругов, то разница пройденных объектами расстояний будет равна m · S: S1 – S2 = m · S.
Задачи на движение мимо объекта
В задачах на движение мимо объекта обязательно присутствуют протяженные тела — поезда, туннели, корабли и т. п. Зачастую движущимся объектом является поезд.
Если поезд длиной L движется мимо точечного объекта (столба, светофора, человека), то он проходит расстояние, равное его длине L:
При этом, если точечный объект (пешеход, велосипедист) тоже движется, то совместная скорость равна сумме скоростей, если поезд и объект двигаются в разных направлениях (как в пункте 1), и равна разности скоростей, если они двигаются в одном направлении (как в пункте 2).
Если поезд длиной L1 движется мимо протяженного объекта (туннеля, лесополосы) длиной L2, то он проходит расстояние, равное сумме длин самого поезда и протяженного объекта:
S = L1 + L2 = v0 · t.
При этом, если протяженный объект (например, другой поезд) тоже движется, то совместная скорость равна сумме скоростей, если оба объекта двигаются в разных направлениях, и равна разности скоростей (из большей вычитается меньшая), если они двигаются в одном направлении.
Задачи на движение по течению и против течения
В задачах на движение помимо собственной скорости плывущего тела нужно учитывать скорость течения.
При движении по течению скорость течения прибавляется к скорости плывущего тела: v = v0 + vтеч.
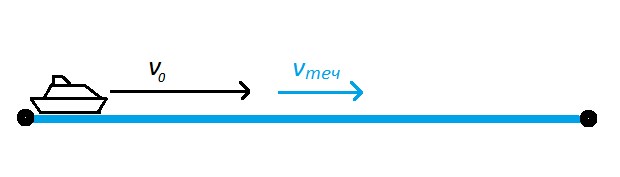
При движении против течения скорость течения отнимается от скорости плывущего тела: v = v0 – vтеч.

Задачи на движение из ЕГЭ по математике (профильный уровень)
Задача 1.
Из одной точки круговой трассы, длина которой равна 44 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 112 км/ч, и через 48 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение: Пусть скорость второго автомобиля равна v км/ч. За 4/5 часа первый автомобиль прошел на 44 км больше, чем второй, отсюда имеем:
112 ∙ alt=»\frac{4}{5}» width=»7″ height=»22″ />= v ∙ alt=»\frac{4}{5}» width=»7″ height=»22″ />+ 44 ⇔ 4 ∙ v = 112 ∙ 4 – 44 ∙ 5 ⇔ v = 57.
Следовательно, скорость второго автомобиля была равна 57 км/ч.
Ответ: 57 км/ч.
Задача 2.
Из пункта A круговой трассы выехал велосипедист, а через 10 минут следом за ним отправился мотоциклист. Через 2 минуты после отправления он догнал велосипедиста в первый раз, а еще через 3 минуты после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 5 км. Ответ дайте в км/ч.
Решение:
До первой встречи велосипедист провел на трассе 1/5 часа, а мотоциклист 1/30 часа. Пусть скорость мотоциклиста равна v км/ч, тогда скорость велосипедиста равна
Тогда если скорость велосипедиста – это 1 единица отношения, то скорость мотоциклиста – это 6 единиц отношения.
Так как они едут в одном направлении, их общая скорость 5 единиц отношения.
∙5 ед.отн. = 5
Таким образом, скорость мотоциклиста была равна 120 км/ч.
Ответ: 120 км/ч.
Задача 3
Часы со стрелками показывают 3 часа ровно. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?
Решение: Скорость движения минутной стрелки 12 делений/час (под одним делением здесь подразумевается расстояние между соседними цифрами на циферблате часов), а часовой ― 1 деление/час. До девятой встречи минутной и часовой стрелок минутная должна сначала 8 раз «обогнать» часовую, то есть пройти 8 кругов по 12 делений. Пусть после этого до четвертой встречи часовая стрелка пройдет L делений. Тогда общий путь минутной стрелки складывается из найденных 96 делений, ещё 3 изначально разделяющих их делений (поскольку часы показывают 3 часа) и последних L делений. Приравняем время движения для часовой и минутной стрелок:
, отсюда и .
Ответ: через 9 минут.
Задача 4
Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение:
Данную задачу можно интерпретировать (представить её, как задачу на линейное движение): Два автомобиля одновременно начинают движение в одном направлении. Скорость первого равна 80 км/ч. Через 40 минут он опережает второго на 14 км (т. к. сказано, что на один круг). Найти скорость второго. Очень важно в заданиях на движение представить сам процесс этого движения.
Сравнение так же производим по расстоянию.
За x принимаем искомую величину ― скорость второго. Время движения 40 минут (2/3 часа) для обоих. Заполним графу «расстояние»:
| v | t | S | |
| 1 | 80 | 2/3 | |
| 2 | x | 2/3 |
Расстояние, пройденное первым, больше расстояния, который прошёл второй на 14 км.
80 ∙ alt=»\frac{2}{3}» width=»7″ height=»22″ />больше, чем x ∙ alt=»\frac{2}{3}» width=»7″ height=»22″ />на 14.
80 ∙ alt=»\frac{2}{3}» width=»7″ height=»22″ />= x ∙ alt=»\frac{2}{3}» width=»7″ height=»22″ />+ 14;
– = x ∙ ;
Скорость второго автомобиля 59 (км/ч).
Ответ: 59 км/ч.
Задача 5
Из пункта A в пункт B, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 6 часов позже автомобилиста. Ответ дайте в км/ч.
Решение:
Пусть v км/ч – скорость велосипедиста, тогда скорость автомобилиста равна v + 40 км/ч. Велосипедист был в пути на 6 часов больше, отсюда имеем:
Тестовые задания на знания основ привил дорожного движения 7-9 классы

Тестовые задания на знание основ правил дорожного движения

7-9 классы
Тестовые задания на знание основ правил дорожного движения
Выберите правильный вариант ответа

1. Выберите правильный вариант ответа.
Пересекать проезжую часть дороги на перекрестках при отсутствии пешеходного перехода пешеходам …
А. Разрешается, при отсутствии транспортных средств на расстоянии 10 метров от перекрестка.
Б. Разрешается на перекрестках по линии тротуаров или обочин.
В. Запрещается.
Самостоятельно дополните определение, используя предложенные варианты

2. Самостоятельно дополните определение, используя предложенные варианты.
Пешеходы, находящиеся вне населенных пунктов, должны иметь при себе __________ и обеспечивать ______ этих предметов _______ транспортных средств.
А. Световозвращающие элементы, видимость, водителям.
Б. Средства пассивной защиты, видимость, пассажирам.
В. Световозвращающие элементы, ношение, водителями.
Выберите правильный вариант ответа

3. Выберите правильный вариант ответа.
Передвигаться в зоне действия знака «Пешеходная зона» разрешено:
А. Только пешеходам.
Б. Пешеходам, велосипедистам в возрасте младше 14 лет.
В. Пешеходам и велосипедистам при отсутствии велосипедной дорожки.
Выберите правильный вариант ответа

4. Выберите правильный вариант ответа.
Дорожный знак, изображенный на рисунке, означает:
А. Запрет на движение велосипедов и мопедов.
Б. Запрет на движение велосипедов.
В. Внимание, велосипедная дорожка.
Посмотрите на изображения дорожных знаков, определите те знаки, которые запрещают движение велосипедистов

5. Посмотрите на изображения дорожных знаков, определите те знаки,
которые запрещают движение велосипедистов.
А. 1, 2.
Б. 2, 3.
В. 2, 4.
Выберите правильный вариант ответа

6. Выберите правильный вариант ответа.
Движение велосипедистов по краю проезжей части осуществляется:
А. По ходу движения транспортных средств.
Б. Навстречу движению транспортных средств.
В. Движение велосипедистов по проезжей части запрещено.
Подберите к каждому изображению оборудования велосипеда правильное место его размещения на самом велосипеде

7. Подберите к каждому изображению оборудования велосипеда правильное место его размещения на самом велосипеде.
В левом столбике изображены виды оборудования, а в правом – части велосипеда. Сопоставьте их между собой.
А. 1-А, 2-Б, 3-В.
Б. 1-Б, 2-В, 3-А.
В. 1-В, 2-А, 3-Б.
Установите по иерархии в порядке убывания, где разрешено движение велосипедистов старше 14 лет:

8. Установите по иерархии в порядке убывания, где разрешено движение велосипедистов старше 14 лет:
По велосипедной, велопешеходной дорожкам.
По тротуару или пешеходной дорожке.
По обочине.
По полосе для велосипедистов.
По правому краю проезжей части.
А. 1, 2, 3, 4, 5.
Б. 1, 5, 3, 4, 2.
В. 1, 4, 5, 3, 2.
Выберете верный вариант ответа (А,

9. Выберете верный вариант ответа (А, Б или В), в котором указана правильная последовательность действий.
Представьте, что Вас попросили проводить пятилетнего соседа Сашу в детский сад. Часть пути предстоит преодолеть на автобусе. Вы дошли до автобусной остановки. Каков дальнейший порядок ваших действий?
Пропустить малыша вперёд.
Пройти первым и подстраховать малыша.
Дождаться полной остановки автобуса и открытия дверей для посадки – высадки.
Занять свободное место, к выходу готовиться заранее.
Дождаться своей очереди выхода из автобуса.
А.3, 1, 4, 3, 5, 2.
Б. 3, 2, 4, 3, 5, 1.
В. 3, 1, 2, 4, 3, 5.
Самостоятельно дополните определение, используя предложенные варианты

10. Самостоятельно дополните определение, используя предложенные варианты.
Понятие «Остановочный путь» транспортного средства подразумевает:
« Расстояние, пройденное ______________ с момента _______________ до полной остановки».
А. транспортным средством, срабатывания тормозного привода.
Б. пешеходом, нажатия водителем транспортного средства педали тормоза.
В. транспортным средством, обнаружения водителем опасности.
Тестовые задания, в которых необходимо выбрать верное утверждение

Тестовые задания, в которых необходимо выбрать верное утверждение.
Определите, какое утверждение верно

1. Определите, какое утверждение верно.
А. Чем ниже скорость автомобиля, тем длиннее его тормозной путь.
Б. Чем выше скорость автомобиля, тем длиннее его тормозной путь.
Определите, какое утверждение верно

2. Определите, какое утверждение верно.
А. Велосипедистам разрешается перевозить груз, выступающий более чем на 0,5 м по длине или ширине только по проезжей части дороги.
Б. Велосипедистам разрешается перевозить груз, выступающий менее чем на 0,5 м по длине или ширине только по проезжей части дороги.
Определите, какое утверждение верно

3. Определите, какое утверждение верно.
А. Мопед — транспортное средство с двигателем внутреннего сгорания рабочим объемом более 50 кубических сантиметров и максимальной конструктивной скоростью не более 60 км/ч.
Б. Мопед — транспортное средство с двигателем внутреннего сгорания рабочим объёмом не более 50 кубических сантиметров и максимальной конструктивной скоростью не более 50 км/ч.
Определите, какое утверждение верно

4. Определите, какое утверждение верно.
А. При усталости водителя внимание ослабляется, время реакции увеличивается.
Б. При усталости водителя внимание ослабляется, время реакции уменьшается.
Определите, какое утверждение верно

5. Определите, какое утверждение верно.
А. Пассажиров в возрасте младше 12 лет запрещается перевозить на заднем сидении мотоцикла.
Б. Пассажиров в возрасте младше 12 лет разрешается перевозить на заднем сидении мотоцикла, если пассажир в застёгнутом шлеме.
Определите, какое утверждение верно

6. Определите, какое утверждение верно.
А. Велосипедистам разрешено перевозить детей в возрасте до 7 лет при отсутствии специально оборудованных для них мест.
Б. Велосипедистам запрещено перевозить детей в возрасте до 7 лет при отсутствии специально оборудованных для них мест.
Определите, какое утверждение верно

7. Определите, какое утверждение верно
А. При движении по дорогам в темное время суток или в условиях недостаточной видимости, пешеходам и велосипедистам рекомендуется использовать световозвращающие элементы.
Б. При движении по дорогам в темное время суток или в условиях недостаточной видимости, пешеходам и велосипедистам необходимо использовать яркую одежду необычных расцветок.
Определите, какое утверждение верно

8. Определите, какое утверждение верно.
А. Лицо, находящееся на самокате, является пешеходом.
Б. Лицо, находящееся на самокате, является водителем.
Определите, какое утверждение верно

9. Определите, какое утверждение верно.
А. Подкачивать шины автомобиля необходимо газовой смесью на основе азота.
Б. Подкачивать шины автомобиля необходимо газовой смесью газовой смесью на основе водорода.
Определите, какое утверждение верно

10. Определите, какое утверждение верно.
А. В зоне действия знаков «Велосипедная зона» и «Конец велосипедной зоны» разрешено движение пешеходов.
Б. В зоне действия знаков «Велосипедная зона» и «Конец велосипедной зоны» запрещено движение пешеходов.
Тестовые задания, в которых описываются ситуации

Тестовые задания, в которых
описываются ситуации
Посмотрите на картинку, проанализируйте ситуацию и определите, как должен поступить пешеход

1. Посмотрите на картинку, проанализируйте ситуацию и определите, как должен поступить пешеход. Выберите правильный ответ.
Кирилл собрался пересечь проезжую часть дороги таким образом, как показывает желтая стрелка на рисунке. Определите, разрешено ли Кириллу пересечь проезжую часть дороги по такой траектории.
А. Разрешено, если в зоне видимости нет перехода или перекрестка и дорога просматривается в обе стороны на достаточном расстоянии.
Б. Разрешено, только в светлое время суток и дорога просматривается в обе стороны.
В. Запрещается.
А. Закончить переход вне зависимости от сигнала светофора, автомобили должны им уступить дорогу

А. Закончить переход вне зависимости от сигнала светофора, автомобили должны им уступить дорогу.
Б. Остановиться на линии, разделяющей транспортные потоки противоположных направлений, дождаться, когда загорится зелёный сигнал пешеходного светофора, и продолжить движение.
В. Пропустив транспортные средства, которые начали движение, закончить переход.
2. Посмотрите на картинку, проанализируйте ситуацию и определите, как должен поступить пешеход. Выберите правильный ответ.
Олег Николаевич и Алиса переходили проезжую часть дороги по регулируемому пешеходному переходу, но не успели закончить переход. Помогите им правильно поступить в данной ситуации.
Посмотрите на картинку, проанализируйте ситуацию и определите, как должен поступить пешеход

3. Посмотрите на картинку, проанализируйте ситуацию и определите, как должен поступить пешеход. Выберите правильный ответ.
Артур идет на встречу с друзьями. Разрешается ли ему движение в данной ситуации?
А. Разрешается, так как он не создает помех велосипедистам.
Б. Разрешается, так как движение может осуществляться, как со стороны велосипедистов, так и со стороны пешеходов.
В. Запрещается, Артуру необходимо перейти на дорожку, расположенную справа от него.
Посмотрите на картинку, проанализируйте ситуацию

4. Посмотрите на картинку, проанализируйте ситуацию. Выберите правильный ответ.
Автобус совершает поворот направо. Как должен поступить велосипедист, который намерен продолжить движение в прямом направлении?
А. Велосипедист должен пропустить автобус, так как он находится в слепой зоне для водителя автобуса.
Б. Убедиться, что водитель автобуса его пропускает, и продолжить движение первым.
В. Сойти с велосипеда, зайти на тротуар, чтобы пропустить автобус.
Посмотрите на картинку, проанализируйте ситуацию

5. Посмотрите на картинку, проанализируйте ситуацию. Выберите правильный ответ.
Автобус находится на автобусной остановке. Разрешено ли велосипедисту объехать автобус в данной ситуации?
А. Разрешено, увеличив скорость, и не создавая помех автобусу.
Б. Разрешено, показав рукой сигнал маневра и не создавая помех другим транспортным средствам.
В. Запрещено.
Посмотрите на картинку, проанализируйте ситуацию

6. Посмотрите на картинку, проанализируйте ситуацию. Выберите правильный ответ.
Алёша выезжает на дорогу, обозначенную знаком «Автомагистраль». Разрешено ли ему в данной ситуации продолжить движение?
А. Разрешено, если на дороге есть полоса для велосипедистов.
Б. Разрешено, если скорость велосипедиста будет больше 60 км/ час.
В. Запрещено.
Посмотрите на картинку, проанализируйте ситуацию

7. Посмотрите на картинку, проанализируйте ситуацию. Выберите правильный ответ.
Разрешается ли велосипедам осуществлять движение как показано на картинке?
А. Разрешается вне населенного пункта ближе к правому краю проезжей части.
Б. Разрешается, при условии отсутствия транспортных средств в пределах видимости велосипедистов.
В. Запрещается, так как велосипедисты должны двигаться в один ряд по правому краю проезжей части.
Посмотрите на картинку, проанализируйте ситуацию

8. Посмотрите на картинку, проанализируйте ситуацию. Выберите правильный ответ.
Коля, которому 16 лет, катает братика Матвея, которому 5 лет, на раме велосипеда, чтобы ему было лучше видно дорогу. Помогите определить, нарушает ли Коля правила дорожного движения.
А. Нарушает, потому что осуществляет перевозку ребенка до 7 лет без детского удерживающего устройства.
Б. Нарушает, потому что осуществляет перевозку ребенка до 7 лет без дополнительного сиденья.
В. Нарушает, потому что осуществляет перевозку ребенка до7 лет без специально оборудованного места.
Посмотрите на картинку, проанализируйте ситуацию

9. Посмотрите на картинку, проанализируйте ситуацию. Выберите правильный ответ.
На картинке изображена мама с сыном, возраста 10 лет, которые едут на мотоцикле по городу. Нарушает ли правила дорожного движения водитель и пассажир?
А. Не нарушают, перевозка детей на заднем сидении мотоцикла возможна с 10 лет.
Б. Нарушают, перевозка детей на заднем сидении мотоцикла возможна с 12 лет.
В. Не нарушают, так как мотоцикл оборудован местом для пассажира и мальчику больше 7 лет.
Посмотрите на картинку, проанализируйте ситуацию

10. Посмотрите на картинку, проанализируйте ситуацию. Выберите правильный ответ.
Посмотрите на картинку, на которой видно, как Иван выходит из такси. Проанализируйте его поведение. Разрешено ли пассажирам осуществлять высадку из транспортного средства таким образом?
А. Запрещено, так как возможна высадка из транспортного средства со стороны тротуара (обочины).
Б. Разрешено, так как высадка из транспортного средства со стороны проезжей части дороги не создаёт видимой опасности.
В. Запрещено, так как высадка из транспортного средства со стороны проезжей части дороги осуществляется в светлое время суток.
Задачи на движение
Продолжаем изучать элементарные задачи по математике. Данный урок посвящен задачам на движение.
Задача на нахождение расстояния/скорости/времени
Задача 1. Автомобиль двигается со скоростью 80 км/ч. Сколько километров он проедет за 3 часа?
Решение
Если за один час автомобиль проезжает 80 километров, то за 3 часа он проедет в три раза больше. Чтобы найти расстояние, нужно скорость автомобиля (80км/ч) умножить на время движения (3ч)
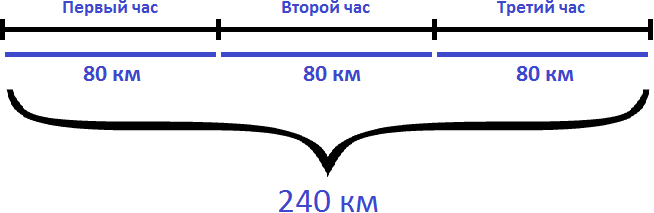
Ответ: за 3 часа автомобиль проедет 240 километров.
Задача 2. На автомобиле за 3 часа проехали 180 км с одной и той же скоростью. Чему равна скорость автомобиля?
Решение
Скорость — это расстояние, пройденное телом за единицу времени. Под единицей подразумевается 1 час, 1 минута или 1 секунда.
Если за 3 часа автомобиль проехал 180 километров с одной и той же скоростью, то разделив 180 км на 3 часа мы определим расстояние, которое проезжал автомобиль за один час. А это есть скорость движения. Чтобы определить скорость, нужно пройденное расстояние разделить на время движения:
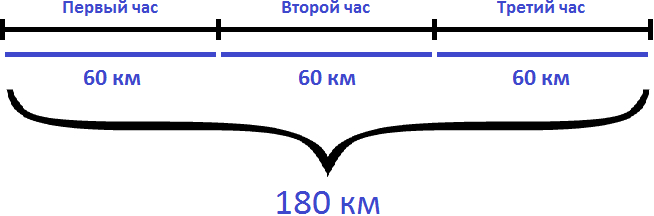
Ответ: скорость автомобиля составляет 60 км/ч
Задача 3. За 2 часа автомобиль проехал 96 км, а велосипедист за 6 часов проехал 72 км. Во сколько раз автомобиль двигался быстрее велосипедиста?
Решение
Определим скорость движения автомобиля. Для этого разделим пройденное им расстояние (96км) на время его движения (2ч)
Определим скорость движения велосипедиста. Для этого разделим пройденное им расстояние (72км) на время его движения (6ч)
Узнаем во сколько раз автомобиль двигался быстрее велосипедиста. Для этого найдем отношение 48 к 12
Ответ: автомобиль двигался быстрее велосипедиста в 4 раза.
Задача 4. Вертолет преодолел расстояние в 600 км со скоростью 120 км/ч. Сколько времени он был в полете?
Решение
Если за 1 час вертолет преодолевал 120 километров, то узнав сколько таких 120 километров в 600 километрах, мы определим сколько времени он был в полете. Чтобы найти время, нужно пройденное расстояние разделить на скорость движения
600 : 120 = 5 часов
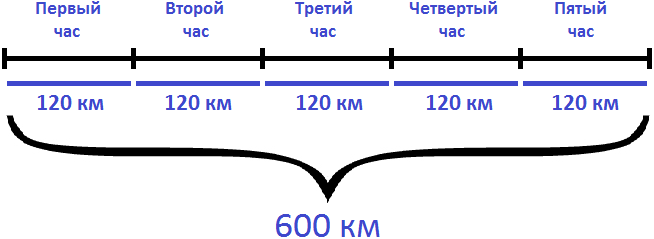
Ответ: вертолет был в пути 5 часов.
Задача 5. Вертолет летел 6 часов со скоростью 160 км/ч. Какое расстояние он преодолел за это время?
Решение
Если за 1 час вертолет преодолевал 160 км, то за 6 часов, он преодолел в шесть раз больше. Чтобы определить расстояние, нужно скорость движения умножить на время
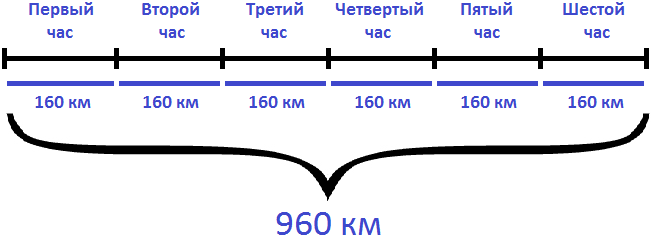
Ответ: за 6 часов вертолет преодолел 960 км.
Задача 6. Расстояние от Перми до Казани, равное 723 км, автомобиль проехал за 13 часов. Первые 9 часов он ехал со скоростью 55 км/ч. Определить скорость автомобиля в оставшееся время.
Решение
Определим сколько километров автомобиль проехал за первые 9 часов. Для этого умножим скорость с которой он ехал первые девять часов (55км/ч) на 9
Определим сколько осталось проехать. Для этого вычтем из общего расстояния (723км) расстояние, пройденное за первые 9 часов движения
723 − 495 = 228 км
Эти 228 километров автомобиль проехал за оставшиеся 4 часа. Чтобы определить скорость автомобиля в оставшееся время, нужно 228 километров разделить на 4 часа:
Ответ: скорость автомобиля в оставшееся время составляла 57 км/ч
Скорость сближения
Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причем скорость первого будет 100 м/м , а второго — 105 м/м , то скорость сближения будет составлять 100 + 105 , то есть 205 м/м . Это значит, что каждую минуту расстояние между пешеходами будет уменьшáться на 205 метров

Чтобы найти скорость сближения, нужно сложить скорости объектов.
Предположим, что пешеходы встретились через три минуты после начала движения. Зная, что они встретились через три минуты, мы можем узнать расстояние между двумя пунктами.
Каждую минуту пешеходы преодолевали расстояние равное двухсот пяти метрам. Через 3 минуты они встретились. Значит умножив скорость сближения на время движения, можно определить расстояние между двумя пунктами:
205 × 3 = 615 метров
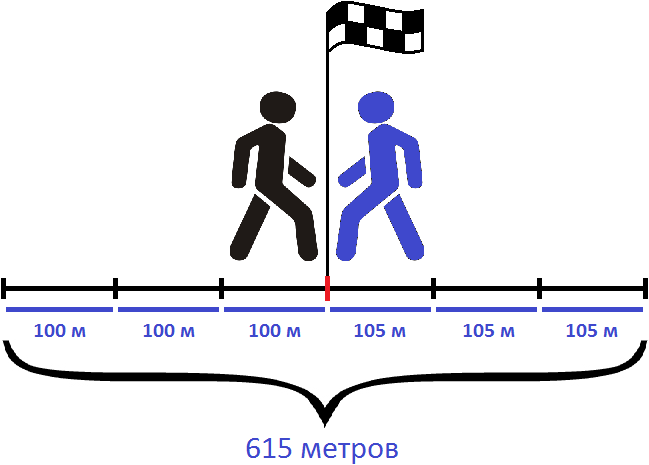
Можно и по другому определить расстояние между пунктами. Для этого следует найти расстояние, которое прошел каждый пешеход до встречи.
Так, первый пешеход шел со скоростью 100 метров в минуту. Встреча состоялась через три минуты, значит за 3 минуты он прошел 100 × 3 метров
100 × 3 = 300 метров
А второй пешеход шел со скоростью 105 метров в минуту. За три минуты он прошел 105 × 3 метров
105 × 3 = 315 метров
Теперь можно сложить полученные результаты и таким образом определить расстояние между двумя пунктами:
300 м + 315 м = 615 м
Задача 1. Из двух населенных пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 10 км/ч, а скорость второго — 12 км/ч. Через 2 часа они встретились. Определите расстояние между населенными пунктами
Решение
Найдем скорость сближения велосипедистов
10 км/ч + 12 км/ч = 22 км/ч
Определим расстояние между населенными пунктами. Для этого скорость сближения умножим на время движения
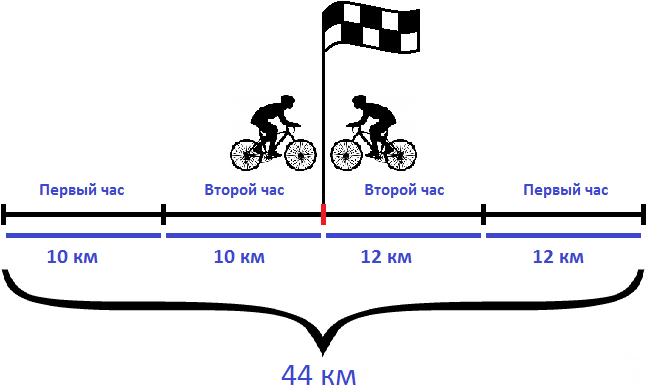
Решим эту задачу вторым способом. Для этого найдем расстояния, пройденные велосипедистами и сложим полученные результаты.
Найдем расстояние, пройденное первым велосипедистом:
Найдем расстояние, пройденное вторым велосипедистом:
Сложим полученные расстояния:
20 км + 24 км = 44 км
Ответ: расстояние между населенными пунктами составляет 44 км.
Задача 2. Из двух населенных пунктов, расстояние между которыми 60 км, навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 14 км/ч, а скорость второго — 16 км/ч. Через сколько часов они встретились?
Решение
Найдем скорость сближения велосипедистов:
14 км/ч + 16 км/ч = 30 км/ч
За один час расстояние между велосипедистами уменьшается на 30 километров. Чтобы определить через сколько часов они встретятся, нужно расстояние между населенными пунктами разделить на скорость сближения:
Значит велосипедисты встретились через два часа
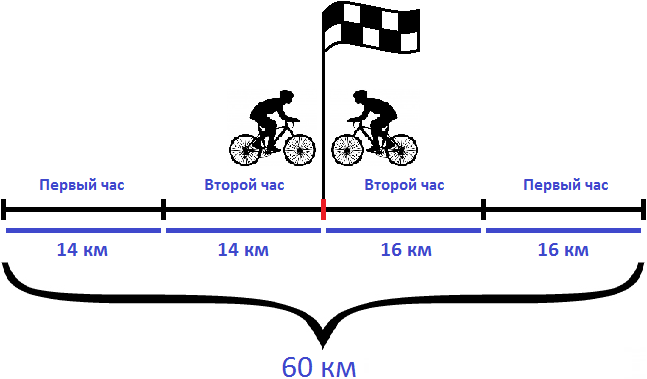
Ответ: велосипедисты встретились через 2 часа.
Задача 3. Из двух населенных пунктов, расстояние между которыми 56 км, навстречу друг другу выехали одновременно два велосипедиста. Через два часа они встретились. Первый велосипедист ехал со скоростью 12 км/ч. Определить скорость второго велосипедиста.
Решение
Определим расстояние пройденное первым велосипедистом. Как и второй велосипедист в пути он провел 2 часа. Умножив скорость первого велосипедиста на 2 часа, мы сможем узнать сколько километров он прошел до встречи
За два часа первый велосипедист прошел 24 км. За один час он прошел 24:2, то есть 12 км. Изобразим это графически
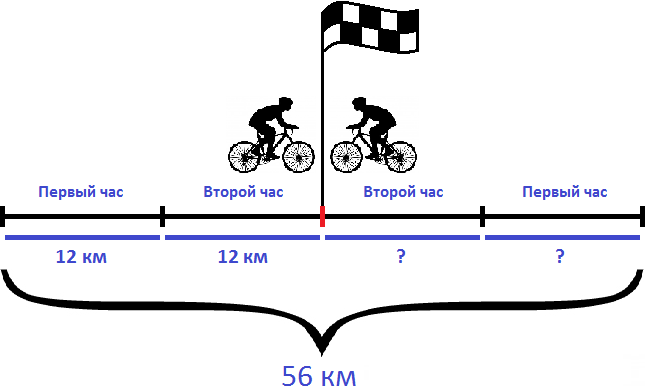
Вычтем из общего расстояния (56 км) расстояние, пройденное первым велосипедистом (24 км). Так мы определим сколько километров прошел второй велосипедист:
56 км − 24 км = 32 км
Второй велосипедист, как и первый провел в пути 2 часа. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
Значит скорость второго велосипедиста составляет 16 км/ч.
Ответ: скорость второго велосипедиста составляет 16 км/ч.
Скорость удаления
Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причем скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4+6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиться на 10 километров.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Так, за первый час расстояние между пешеходами будет составлять 10 километров. На следующем рисунке можно увидеть, как это происходит
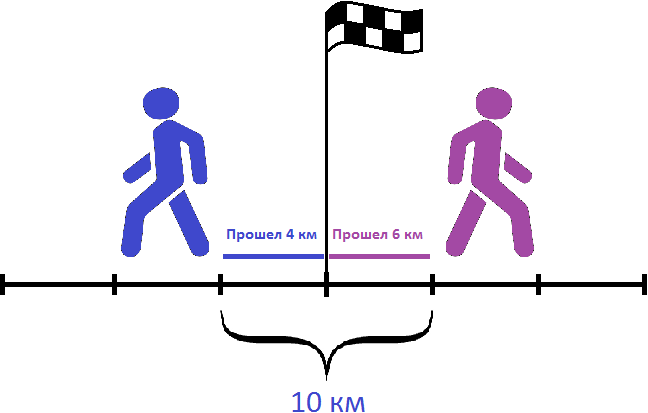
Видно, что первый пешеход прошел свои 4 километра за первый час. Второй пешеход также прошел свои 6 километров за первый час. Итого за первый час расстояние между ними стало 4+6, то есть 10 километров.
Через два часа расстояние между пешеходами будет составлять 10×2, то есть 20 километров. На следующем рисунке можно увидеть, как это происходит:
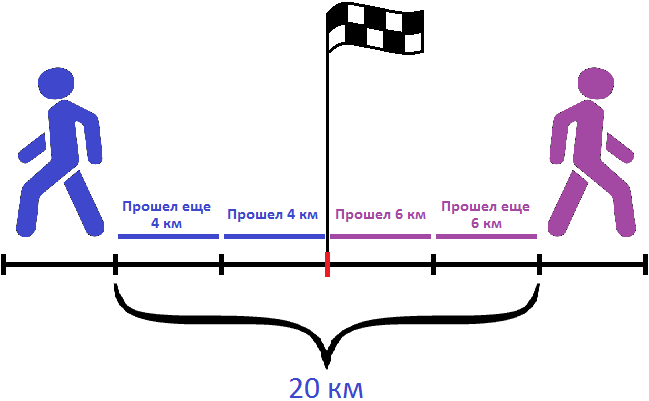
Задача 1. От одной станции отправились одновременно в противоположных направлениях товарный поезд и пассажирский экспресс. Скорость товарного поезда составляла 40 км/ч, скорость экспресса 180 км/ч. Какое расстояние будет между этими поездами через 2 часа?
Решение
Определим скорость удаления поездов. Для этого сложим их скорости:
40 + 180 = 220 км/ч
Получили скорость удаления поездов равную 220 км/ч. Данная скорость показывает, что за час расстояние между поездами будет увеличиваться на 220 километров. Чтобы узнать какое расстояние будет между поездами через два часа, нужно 220 умножить на 2
Ответ: через 2 часа расстояние будет между поездами будет 440 километров.
Задача 2. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 16 км/ч, а скорость мотоциклиста — 40 км/ч. Какое расстояние будет между велосипедистом и мотоциклистом через 2 часа?
Решение
Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:
16 км/ч + 40 км/ч = 56 км/ч
Определим расстояние, которое будет между велосипедистом и мотоциклистом через 2 часа. Для этого скорость удаления (56км/ч) умножим на 2 часа
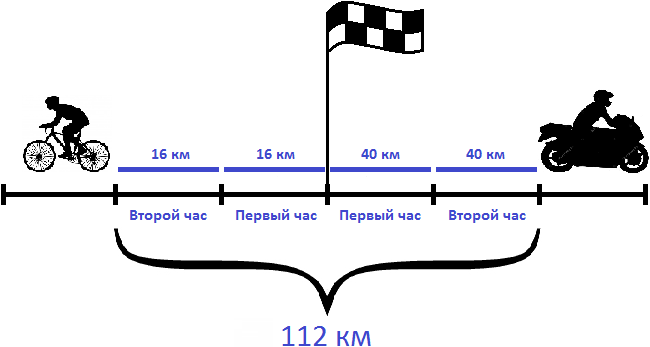
Ответ: через 2 часа расстояние между велосипедистом и мотоциклистом будет 112 км.
Задача 3. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 10 км/ч, а скорость мотоциклиста — 30 км/ч. Через сколько часов расстояние между ними будет 80 км?
Решение
Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:
10 км/ч + 30 км/ч = 40 км/ч
За один час расстояние между велосипедистом и мотоциклистом увеличивается на 40 километров. Чтобы узнать через сколько часов расстояние между ними будет 80 км, нужно определить сколько раз 80 км содержит по 40 км
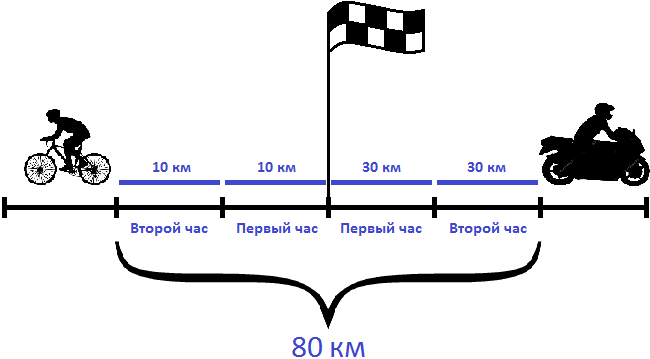
Ответ: через 2 часа после начала движения, между велосипедистом и мотоциклистом будет 80 километров.
Задача 4. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Через 2 часа расстояние между ними было 90 км. Скорость велосипедиста составляла 15 км/ч. Определить скорость мотоциклиста
Решение
Определим расстояние, пройденное велосипедистом за 2 часа. Для этого умножим его скорость (15 км/ч) на 2 часа
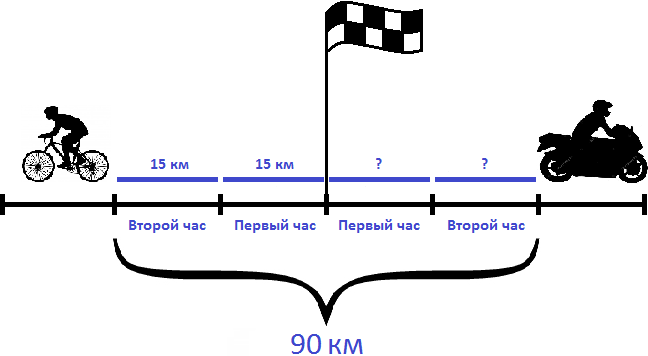
На рисунке видно, что велосипедист прошел по 15 километров в каждом часе. Итого за два часа он прошел 30 километров.
Вычтем из общего расстояния (90 км) расстояние, пройденное велосипедистом (30 км). Так мы определим сколько километров прошел мотоциклист:
90 км − 30 км = 60 км
Мотоциклист за два часа прошел 60 километров. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
Значит скорость мотоциклиста составляла 30 км/ч.
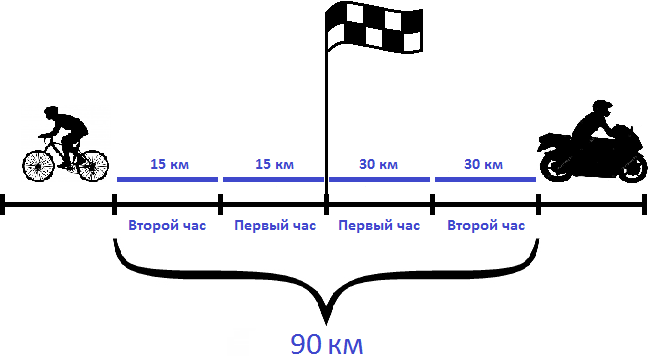
Ответ: скорость мотоциклиста составляла 30 км/ч.
Задача на движение объектов в одном направлении
В предыдущей теме мы рассматривали задачи в которых объекты (люди, машины, лодки) двигались либо навстречу другу другу либо в противоположных направлениях. При этом мы находили различные расстояния, которые изменялись между объектами в течении определенного времени. Эти расстояния были либо скоростями сближения либо скоростями удаления.
В первом случае мы находили скорость сближения — в ситуации, когда два объекта двигались навстречу друг другу. За единицу времени расстояние между объектами уменьшалось на определенное расстояние

Во втором случае мы находили скорость удаления — в ситуации, когда два объекта двигались в противоположных направлениях. За единицу времени расстояние между объектами увеличивалось на определенное расстояние

Но объекты также могут двигаться в одном направлении, причем с различной скоростью. Например, из одного пункта одновременно могут выехать велосипедист и мотоциклист, причем скорость велосипедиста может составлять 20 километров в час, а скорость мотоциклиста — 40 километров в час
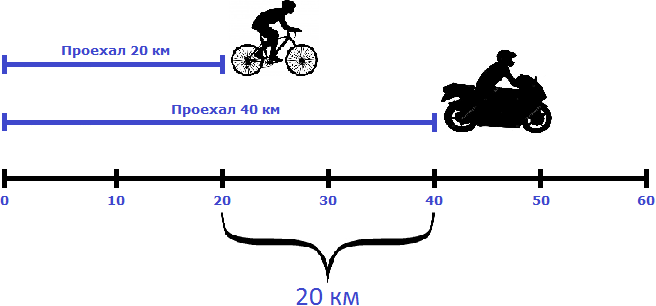
На рисунке видно, что мотоциклист впереди велосипедиста на двадцать километров. Связано это с тем, что в час он преодолевает на 20 километров больше, чем велосипедист. Поэтому каждый час расстояние между велосипедистом и мотоциклистом будет увеличиваться на двадцать километров.
В данном случае 20 км/ч являются скоростью удаления мотоциклиста от велосипедиста.
Через два часа расстояние, пройденное велосипедистом будет составлять 40 км. Мотоциклист же проедет 80 км, отдалившись от велосипедиста еще на двадцать километров — итого расстояние между ними составит 40 километров
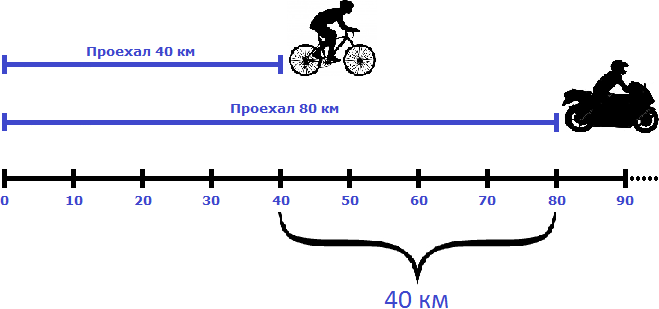
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
В приведенном выше примере, скорость удаления составляет 20 км/ч. Её можно найти путем вычитания скорости велосипедиста из скорости мотоциклиста. Скорость велосипедиста составляла 20 км/ч, а скорость мотоциклиста — 40 км/ч. Скорость мотоциклиста больше, поэтому из 40 вычитаем 20
40 км/ч − 20 км/ч = 20 км/ч
Задача 1. Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 120 км/ч, а скорость автобуса 80 км/ч. Какое расстояние будет между ними через 1 час? 2 часа?
Решение
Найдем скорость удаления. Для этого из большей скорости вычтем меньшую
120 км/ч − 80 км/ч = 40 км/ч
Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 2 часа в два раза больше:
Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через два часа — 80 км.
Рассмотрим ситуацию в которой объекты начали свое движение из разных пунктов, но в одном направлении.
Пусть имеется дом, школа и аттракцион. От дома до школы 700 метров
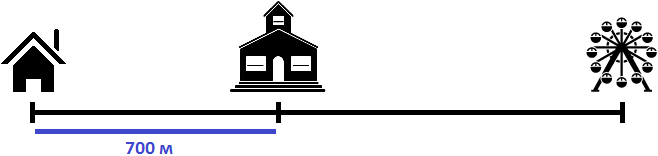
Два пешехода отправились в аттракцион в одно и то же время. Причем первый пешеход отправился в аттракцион от дома со скоростью 100 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 80 метров в минуту. Какое расстояние будет между пешеходами через 2 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Ответим на первый вопрос задачи — какое расстояние будет между пешеходами через 2 минуты?
Определим расстояние, пройденное первым пешеходом за 2 минуты. Он двигался со скоростью 100 метров в минуту. За две минуты он пройдет в два раза больше, то есть 200 метров
100 × 2 = 200 метров
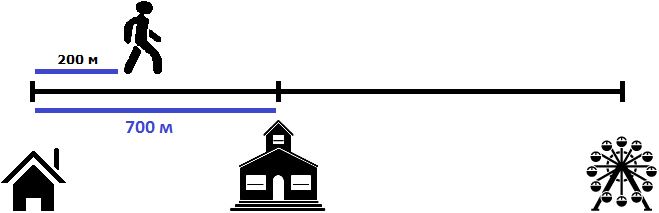
Определим расстояние, пройденное вторым пешеходом за 2 минуты. Он двигался со скоростью 80 метров в минуту. За две минуты он пройдет в два раза больше, то есть 160 метров
80 × 2 = 160 метров
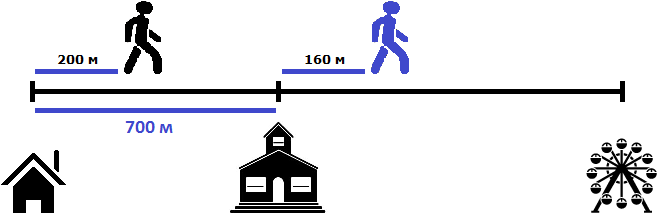
Теперь нужно найти расстояние между пешеходами
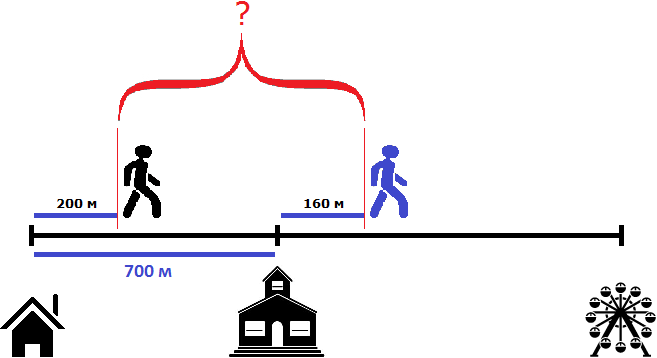
Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (700м) прибавить расстояние, пройденное вторым пешеходом (160м) и из полученного результата вычесть расстояние, пройденное первым пешеходом (200м)
700 м + 160 м = 860 м
860 м − 200 м = 660 м
Либо из расстояния от дома до школы (700м) вычесть расстояние, пройденное первым пешеходом (200м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (160м)
700 м − 200 м = 500 м
500 м + 160 м = 660 м
Таким образом, через две минуты расстояние между пешеходами будет составлять 660 метров
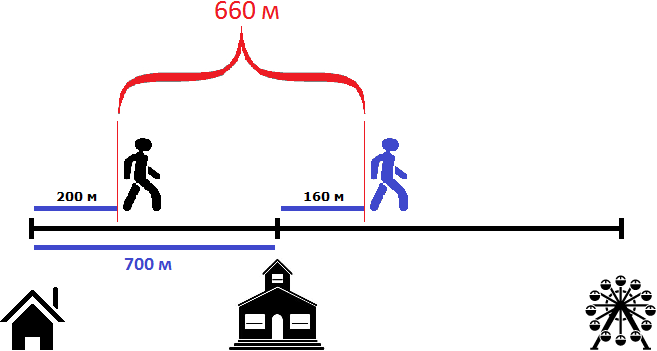
Попробуем ответить на следующий вопрос задачи: через сколько минут после начала движения первый пешеход догонит второго?
Давайте посмотрим какой была ситуация в самом начале пути — когда пешеходы еще не начали своё движение
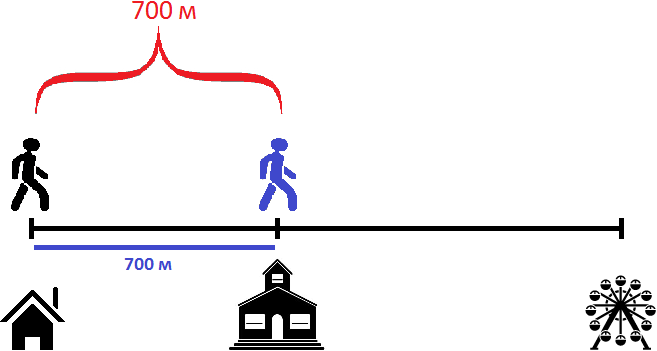
Как видно на рисунке, расстояние между пешеходами в начале пути составляло 700 метров. Но уже через минуту после начала движения расстояние между ними будет составлять 680 метров, поскольку первый пешеход двигается на 20 метров быстрее второго:
100 м × 1 = 100 м
700 м + 80 м − 100 м = 780 м − 100 м = 680 м
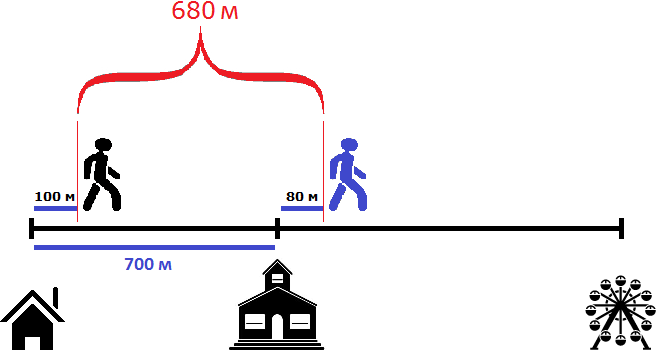
Через две минуты после начала движения, расстояние уменьшится еще на 20 метров и будет составлять 660 метров. Это был наш ответ на первый вопрос задачи:
100 м × 2 = 200 м
700 м + 160 м − 200м = 860 м − 200 м = 660 м

Через три минуты расстояние уменьшится еще на 20 метров и будет уже составлять 640 метров:
100 м × 3 = 300 м
700 м + 240 м − 300м = 940 м − 300 м = 640 м
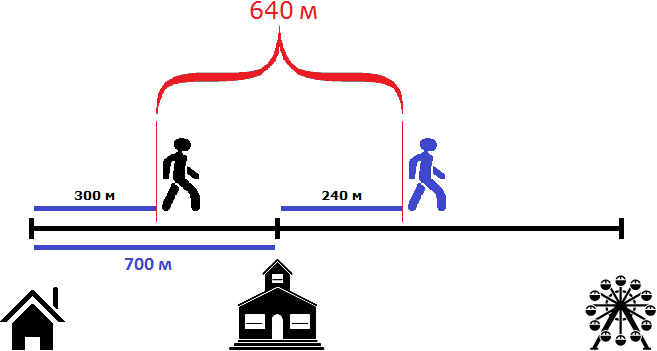
Мы видим, что с каждой минутой первый пешеход будет приближáться ко второму на 20 метров, и в конце концов догонит его. Можно сказать, что скорость равная двадцати метрам в минуту является скоростью сближения пешеходов. Правила нахождения скорости сближения и удаления при движении в одном направлении идентичны.
Чтобы найти скорость сближения при движении в одном направлении, нужно из большей скорости вычесть меньшую.
А раз изначальные 700 метров с каждой минутой уменьшаются на одинаковые 20 метров, то мы можем узнать сколько раз 700 метров содержат по 20 метров, тем самым определяя через сколько минут первый пешеход догонит второго
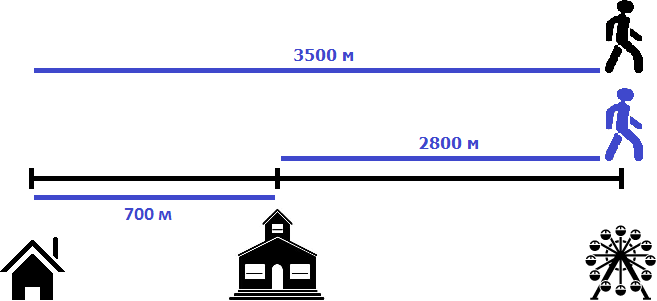
Значит через 35 минут после начала движения первый пешеход догонит второго. Для интереса узнаем сколько метров прошел к этому времени каждый пешеход. Первый двигался со скоростью 100 метров в минуту. За 35 минут он прошел в 35 раз больше
100 × 35 = 3500 м
Второй шел со скоростью 80 метров в минуту. За 35 минут он прошел в 35 раз больше
Первый прошел 3500 метров, а второй 2800 метров. Первый прошел на 700 метров больше, поскольку он шел от дома. Если вычесть эти 700 метров из 3500, то мы получим 2800 м
Рассмотрим ситуацию в которой объекты движутся в одном направлении, но один из объектов начал своё движение раньше другого.
Пусть имеется дом и школа. Первый пешеход отправился в школу со скоростью 80 метров в минуту. Через 5 минут вслед за ним в школу отправился второй пешеход со скоростью 100 метров в минуту. Через сколько минут второй пешеход догонит первого?
Второй пешеход начал свое движение через 5 минут. К этому времени первый пешеход уже отдалился от него на какое-то расстояние. Найдём это расстояние. Для этого умножим его скорость (80 м/м) на 5 минут
80 × 5 = 400 метров
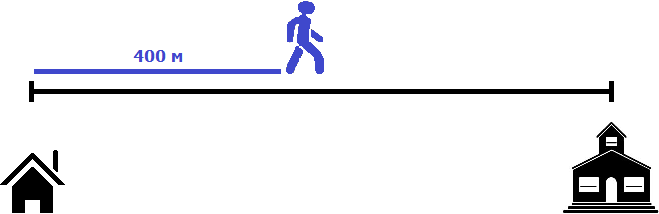
Первый пешеход отдалился от второго на 400 метров. Поэтому в момент, когда второй пешеход начнет свое движение, между ними будут эти самые 400 метров.
Но второй пешеход двигается со скоростью 100 метров в минуту. То есть двигается на 20 метров быстрее первого пешехода, а значит с каждой минутой расстояние между ними будет уменьшáться на 20 метров. Наша задача узнать через сколько минут это произойдет.
Например, уже через минуту расстояние между пешеходами будет составлять 380 метров. Первый пешеход к своим 400 метрам пройдет еще 80 метров, а второй пройдет 100 метров
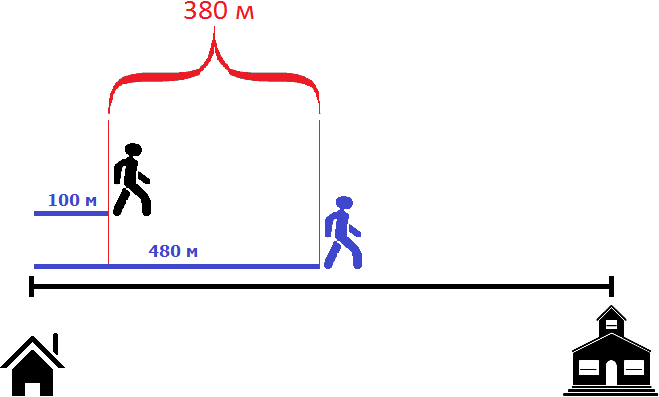
Принцип здесь такой-же, как и в предыдущей задаче. Расстояние между пешеходами в момент движения второго пешехода необходимо разделить на скорость сближения пешеходов. Скорость сближения в данном случае равна двадцати метрам. Поэтому, чтобы определить через сколько минут второй пешеход догонит первого, нужно 400 метров разделить на 20
Значит через 20 минут второй пешеход догонит первого.
Задача 2. Из двух сел, расстояние между которыми 40 км, одновременно в одном направлении выехали автобус и велосипедист. Скорость велосипедиста 15 км/ч, а скорость автобуса 35 км/ч. Через сколько часов автобус догонит велосипедиста?
Решение
Найдем скорость сближения
35 км/ч − 15 км/ч = 20 км/ч
Определим через часов автобус догонит велосипедиста
Ответ: автобус догонит велосипедиста через 2 часа.
Задача на движение по реке
Суда двигаются по реке с различной скоростью. При этом они могут двигаться, как по течению реки, так и против течения. В зависимости от того, как они двигаются (по или против течения), скорость будет меняться.
Предположим, что скорость реки составляет 3 км/ч. Если спустить лодку на реку, то река унесет лодку со скоростью 3 км/ч.
Если спустить лодку на стоячую воду, в которой отсутствует течение, то и лодка будет стоять. Скорость движения лодки в этом случае будет равна нулю.
Если лодка плывет по стоячей воде, в которой отсутствует течение, то говорят, что лодка плывет с собственной скоростью.
Например, если моторная лодка плывет по стоячей воде со скоростью 40 км/ч, то говорят что собственная скорость моторной лодки составляет 40 км/ч.
Как определить скорость судна?
Если судно плывет по течению реки, то к собственной скорости судна нужно прибавить скорость течения реки.
Например, если моторная лодка плывет со скоростью 30 км/ч по течению реки, и скорость течения реки составляет 2 км/ч, то к собственной скорости моторной лодки (30 км/ч) необходимо прибавить скорость течения реки (2 км/ч)
30 км/ч + 2 км/ч = 32 км/ч
Течение реки можно сказать помогает моторной лодке дополнительной скоростью равной двум километрам в час.
Если судно плывет против течения реки, то из собственной скорости судна нужно вычесть скорость течения реки.
Например, если моторная лодка плывет со скоростью 30 км/ч против течения реки, и скорость течения реки составляет 2 км/ч, то из собственной скорости моторной лодки (30 км/ч) необходимо вычесть скорость течения реки (2 км/ч)
30 км/ч − 2 км/ч = 28 км/ч
Течение реки в этом случае препятствует моторной лодке свободно двигаться вперед, снижая её скорость на два километра в час.
Задача 1. Скорость катера 40 км/ч, а скорость течения реки 3 км/ч. С какой скоростью катер будет двигаться по течению реки? Против течения реки?
Ответ:
Если катер будет двигаться по течения реки, то скорость его движения составит 40 + 3, то есть 43 км/ч.
Если катер будет двигаться против течения реки, то скорость его движения составит 40 − 3, то есть 37 км/ч.
Задача 2. Скорость теплохода в стоячей воде — 23 км/ч. Скорость течения реки — 3 км/ч. Какой путь пройдет теплоход за 3 часа по течению реки? Против течения?
Решение
Собственная скорость теплохода составляет 23 км/ч. Если теплоход будет двигаться по течению реки, то скорость его движения составит 23 + 3, то есть 26 км/ч. За три часа он пройдет в три раза больше
Если теплоход будет двигаться против течения реки, то скорость его движения составит 23 − 3, то есть 20 км/ч. За три часа он пройдет в три раза больше
Задача 3. Расстояние от пункта А до пункта B лодка преодолела за 3 часа 20 минут, а расстояние от пункта B до А — за 2 часа 50 минут. В каком направлении течет река: от А к В или от В к А, если известно, что скорость яхты не менялась?
Решение
Скорость яхты не менялась. Узнаем на какой путь она затратила больше времени: на путь от А до В или на путь от В до А. Тот путь, который затратил больше времени будет тем путем, течение реки которого шло против яхты
3 часа 20 минут больше, чем 2 часа 50 минут. Это значит, что течение реки снизило скорость яхты и это отразилось на времени пути. 3 часа 20 минут это время, затраченное на путь от от А до В. Значит река течет от пункта B к пункту А
Задача 4. За какое время при движении против течения реки
теплоход пройдет 204 км, если его собственная скорость
15 км/ч, а скорость течения в 5 раз меньше собственной
скорости теплохода?
Решение
Требуется найти время за которое теплоход пройдет 204 километра против течения реки. Собственная скорость теплохода составляет 15 км/ч. Двигается он против течения реки, поэтому нужно определить его скорость при таком движении.
Чтобы определить скорость против течения реки, нужно из собственной скорости теплохода (15 км/ч) вычесть скорость движения реки. В условии сказано, что скорость течения реки в 5 раз меньше собственной скорости теплохода, поэтому сначала определим скорость течения реки. Для этого уменьшим 15 км/ч в пять раз
Скорость течения реки составляет 3 км/ч. Вычтем эту скорость из скорости движения теплохода
15 км/ч − 3 км/ч = 12 км/ч
Теперь определим время за которое теплоход пройдет 204 км при скорости 12 км/ч. В час теплоход проходит 12 километров. Чтобы узнать за сколько часов он пройдет 204 километра, нужно определить сколько раз 204 километра содержит по 12 километров
Ответ: теплоход пройдет 204 километра за 17 часов
Задача 5. Двигаясь по течению реки, за 6 часов лодка
прошла 102 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.
Решение
Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (102км) разделим на время движения (6ч)
Определим собственную скорость лодки. Для этого из скорости по которой она двигалась по реке (17 км/ч) вычтем скорость течения реки (4 км/ч)
Задача 6. Двигаясь против течения реки, за 5 часов лодка
прошла 110 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.
Решение
Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (110км) разделим на время движения (5ч)
Определим собственную скорость лодки. В условии сказано, что она двигалась против течения реки. Скорость течения реки составляла 4 км/ч. Это значит, что собственная скорость лодки была уменьшена на 4. Наша задача прибавить эти 4 км/ч и узнать собственную скорость лодки
Ответ: собственная скорость лодки составляет 26 км/ч
Задача 7. За какое время при движении против течения реки лодка
пройдет 56 км, если скорость течения – 2 км/ч, а её
собственная скорость на 8 км/ч больше скорости течения?
Решение
Найдем собственную скорость лодки. В условии сказано, что она на 8 км/ч больше скорости течения. Поэтому для определения собственной скорости лодки, к скорости течения (2 км/ч) прибавим еще 8 км/ч
2 км/ч + 8 км/ч = 10 км/ч
Лодка движется против течения реки, поэтому из собственной скорости лодки (10 км/ч) вычтем скорость движения реки (2 км/ч)
10 км/ч − 2 км/ч = 8 км/ч
Узнаем за какое время лодка пройдет 56 км. Для этого расстояние (56км) разделим на скорость движения лодки:
Ответ: при движении против течения реки лодка пройдет 56 км за 7 часов
Задачи для самостоятельного решения
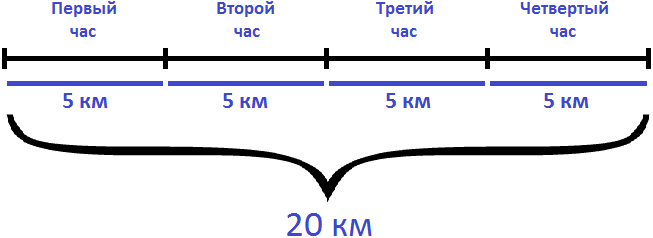
Решение
За один час пешеход проходит 5 километров. Чтобы определить за какое время он пройдет 20 км, нужно узнать сколько раз 20 километров содержат по 5 км. Либо воспользоваться правилом нахождения времени: разделить пройденное расстояние на скорость движения
Решение
Определим расстояние от пункта А до пункта В. Для этого умножим скорость с которой ехал велосипедист из пункта А в пункт В (16км/ч) на время движения (5ч)
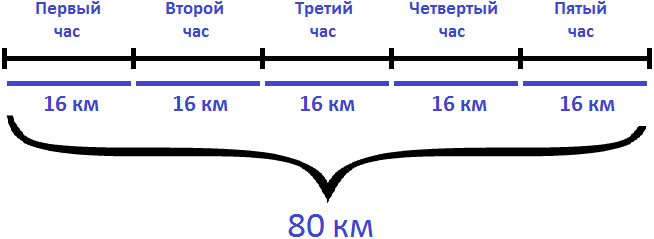
Определим сколько времени велосипедист затратил на обратный путь. Для этого расстояние (80км) разделим на скорость движения (10км/ч)
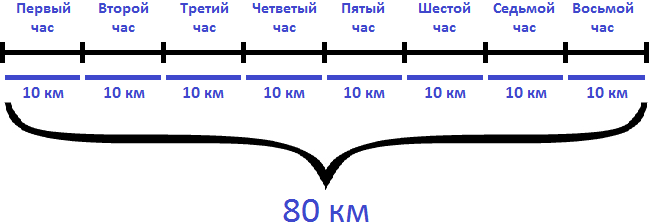
Решение
Определим путь, пройденный велосипедистом за 6 часов. Для этого из 83 км вычтем путь, который он прошел после шести часов движения (11км)
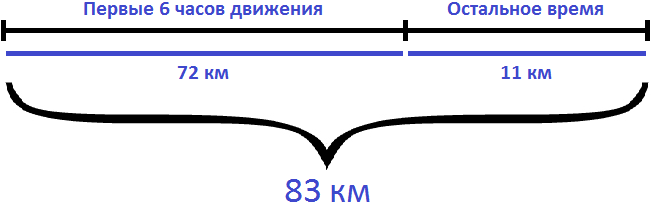
Определим с какой скоростью ехал велосипедист первые 6 часов. Для этого разделим 72 км на 6 часов
Поскольку в условии задаче сказано, что остальные 11 км велосипедист проехал с той же скоростью, что и в первые 6 часов движения, то скорость равная 12 км/ч является ответом к задаче.
Ответ: велосипедист ехал со скоростью 12 км/ч.
Решение
Найдем скорость течения реки. В условии сказано, что плот может проплыть 72 километра за 36 часов. Плот не может двигаться против течения реки. Значит скорость плота с которой он преодолевает эти 72 километра и является скоростью течения реки. Чтобы найти эту скорость, нужно 72 километра разделить на 36 часов
Найдем собственную скорость теплохода. Сначала найдем скорость его движения против течения реки. Для этого разделим 72 километра на 4 часа
Если против течения реки скорость теплохода составляет 18 км/ч, то собственная его скорость равна 18+2, то есть 20 км/ч. А по течению реки его скорость будет составлять 20+2, то есть 22 км/ч
Разделив 110 километров на скорость движения теплохода по течению реки (22 км/ч), можно узнать за сколько часов теплоход проплывет эти 110 километров
Ответ: по течению реки теплоход проплывет 110 километров за 5 часов.
Решение
Найдем скорость удаления велосипедистов
Узнаем какое расстояние будет между ними через 4 часа
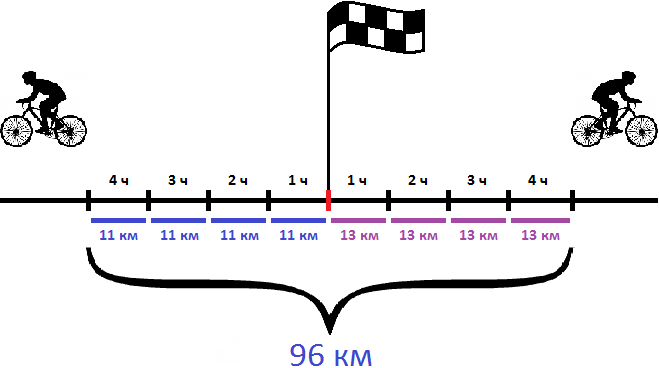
Ответ: через 4 часа расстояние между велосипедистами будет 96 км.
Решение
Определим расстояние, пройденное первым теплоходом. Для этого умножим его скорость (21 км/ч) на время движения до встречи (6ч)
Определим расстояние, пройденное вторым теплоходом. Для этого умножим его скорость (24 км/ч) на время движения до встречи (6ч)
Определим расстояние между пристанями. Для этого сложим расстояния, пройденные первым и вторым теплоходами
126 км + 144 км = 270 км
Ответ: первый теплоход прошел 126 км, второй — 144 км. Расстояние между пристанями составляет 270 км.
Решение
Определим сколько километров до встречи прошел поезд, вышедший из Москвы. Для этого умножим его скорость (51 км/ч) на 16 часов
Узнаем сколько километров до встречи прошел поезд, вышедший из Уфы. Для этого из расстояния между Москвой и Уфой (1520км) вычтем расстояние, пройденное поездом, вышедшим из Москвы
1520 − 816 = 704 км
Определим скорость с которой шел поезд, вышедший из Уфы. Для этого расстояние, пройденное им до встречи, нужно разделить на 16 часов
704 : 16 = 44 км/ч
Определим расстояние, которое будет между поездами через 5 часов после их встречи. Для этого найдем скорость удаления поездов и умножим эту скорость на 5
51 км/ч + 44 км/ч = 95 км/ч
Ответ: поезд, вышедший из Уфы, шел со скоростью 44 км/ч. Через 5 часов после их встречи поездов расстояние между ними будет составлять 475 км.
Решение
Найдем скорость второго автобуса. Она на 6 км/ч больше скорости первого автобуса
48 км/ч + 6 км/ч = 54 км/ч
Найдем скорость удаления автобусов. Для этого сложим их скорости:
48 км/ч + 54 км/ч = 102 км/ч
За час расстояние между автобусами увеличивается на 102 километра. Чтобы узнать через сколько часов расстояние между ними будет 510 км, нужно узнать сколько раз 510 км содержит по 102 км/ч
Ответ: 510 км между автобусами будет через 5 часов.
Задача 9. Расстояние от Ростова-на-Дону до Москвы 1230 км. Из Москвы и Ростова навстречу друг другу вышли два поезда. Поезд из Москвы идет со скоростью 63 км/ч, а скорость ростовского поезда составляет скорости московского поезда. На каком расстоянии от Ростова встретятся поезда?
Решение
Найдем скорость ростовского поезда. Она составляет />скорости московского поезда. Поэтому чтобы определить скорость ростовского поезда, нужно найти />от 63 км
63 : 21 × 20 = 3 × 20 = 60 км/ч
Найдем скорость сближения поездов
63 км/ч + 60 км/ч = 123 км/ч
Определим через сколько часов поезда встретятся
1230 : 123 = 10 ч
Узнаем на каком расстоянии от Ростова встретятся поезда. Для этого достаточно найти расстояние, пройденное ростовским поездом до встречи
Ответ: поезда встретятся на расстоянии 600 км от Ростова.
Решение
Найдем скорость второй лодки. Она составляет 75% скорости первой лодки. Поэтому чтобы найти скорость второй лодки, нужно 75% от 16 км
16 × 0,75 = 12 км/ч
Найдем скорость сближения лодок
16 км/ч + 12 км/ч = 28 км/ч
С каждым часом расстояние между лодками будет уменьшáться на 28 км. Через 2 часа оно уменьшится на 28×2, то есть на 56 км. Чтобы узнать какое будет расстояние между лодками в этот момент, нужно из 75 км вычесть 56 км
75 км − 56 км = 19 км
Ответ: через 2 часа между лодками будет 19 км.
Решение
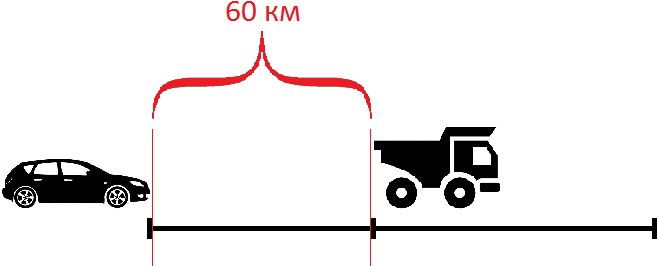
Найдем скорость сближения
62 км/ч − 47 км/ч = 15 км/ч
Если первоначально расстояние между машинами было 60 километров, то с каждым часом это расстояние будет уменьшáться на 15 км, и в конце концов легковая машина догонит грузовую. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 60 км содержит по 15 км
Узнаем на каком расстоянии от начала движения легковая машина догнала грузовую. Для этого умножим скорость легковой машины (62 км/ч) на время её движения до встречи (4ч)
Ответ: легковая машина догонит грузовую через 4 часа. В момент встречи легковая машина будет на расстоянии 248 км от начала движения.
Решение
Найдем скорость второго мотоциклиста. Она составляет 80% скорости первого мотоциклиста. Поэтому чтобы найти скорость второго мотоциклиста, нужно найти 80% от 35 км/ч
35 × 0,80 = 28 км/ч
Первый мотоциклист двигается на 35-28 км/ч быстрее
35 км/ч − 28 км/ч = 7 км/ч
За один час первый мотоциклиста преодолевает на 7 километров больше. С каждым часом она будет приближáться ко второму мотоциклисту на эти 7 километров.
Через 5 часов первый мотоциклист пройдет 35×5, то есть 175 км, а второй мотоциклист пройдет 28×5, то есть 140 км. Определим расстояние, которое между ними. Для этого из 175 км вычтем 140 км
175 − 140 = 35 км
Ответ: через 5 часов расстояние между мотоциклистами будет 35 км.
Решение
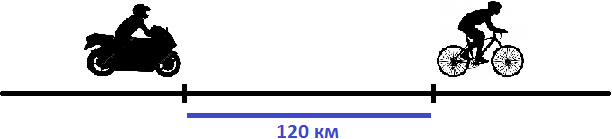
Найдем скорость сближения:
43 км/ч − 13 км/ч = 30 км/ч
Если первоначально расстояние между мотоциклистом и велосипедистом было 120 километров, то с каждым часом это расстояние будет уменьшáться на 30 км, и в конце концов мотоциклист догонит велосипедиста. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 120 км содержит по 30 км
Значит через 4 часа мотоциклист догонит велосипедиста
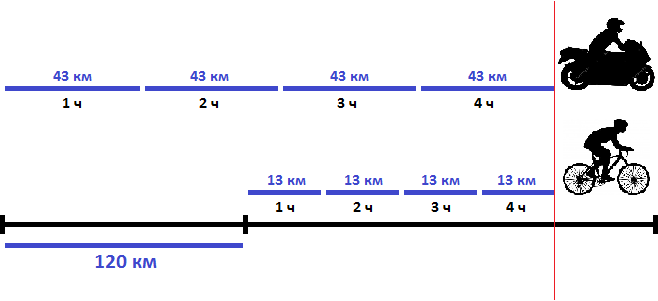
На рисунке представлено движение мотоциклиста и велосипедиста. Видно, что через 4 часа после начала движения они сровнялись.
Ответ: мотоциклист догонит велосипедиста через 4 часа.
Решение
Определим скорость велосипедиста, ехавшего впереди. Для этого найдем 75% от скорости велосипедиста, ехавшего сзади:
12 × 0,75 = 9 км/ч — скорость ехавшего впереди
Узнаем сколько километров проехал каждый велосипедист до того, как второй догнал первого:
12 × 6 = 72 км — проехал ехавший сзади
9 × 6 = 54 км — проехал ехавший впереди
Узнаем какое расстояние было между велосипедистами первоначально. Для этого из расстояния, пройденного вторым велосипедистом (который догонял) вычтем расстояние, пройденное первым велосипедистом (которого догнали)
72 км − 54 км = 18 км
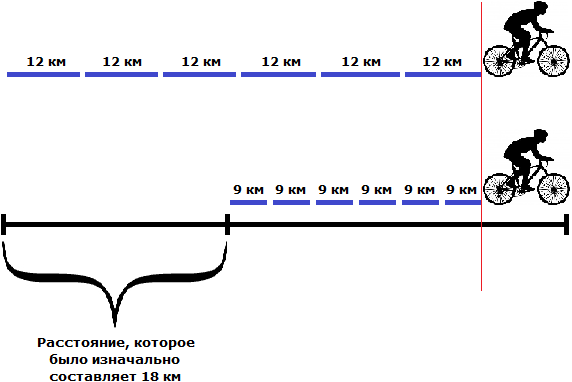
Ответ: между велосипедистами первоначально было 18 км.
Решение
Найдем скорость удаления автомобиля от автобуса
53 км/ч − 41 км/ч = 12 км/ч
С каждым часом автомобиль будет удаляться от автобуса на 12 километров. На рисунке показано положение машин после первого часа движения
Видно, что автомобиль впереди автобуса на 12 км.
Чтобы узнать через сколько часов автомобиль будет впереди автобуса на 48 километров, нужно определить сколько раз 48 км содержит по 12 км
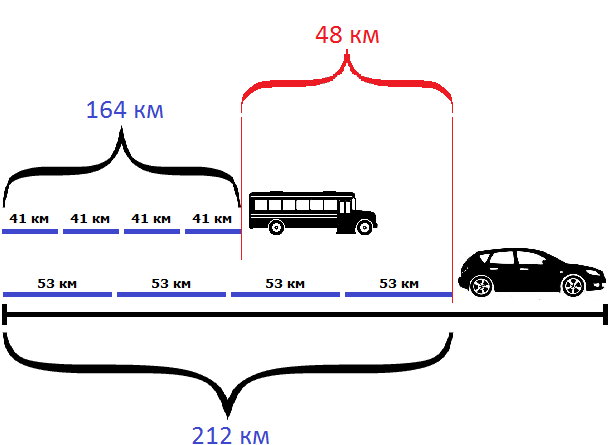
Ответ: через 4 часа после выезда автомобиль будет впереди автобуса на 48 километров.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
19 thoughts on “Задачи на движение”
Здравствуйте. Как решить такую задачу? Она вроде, и на движение, и на уравнение, но никак не мог понять как ее составить и решить.
Моторная лодка прошла против течения реки 297 км и вернулась в пункт отправления, затратив на обратный путь на 3 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 2 км/ч.
Задача на составление уравнения, содержащего рациональные выражения. В данном уроке такие задачи не рассмотрены. Обычно их решают в процессе изучения рациональных выражений.
x — скорость лодки в неподвижной воде
x — 2 — скорость лодки против течения
x + 2 — скорость лодки по течению
297/x-2 — время движения против течения
297/x+2 — время движения по течению
Задания №11. Задачи на движение по прямой

На этот раз рассматриваем задачи из открытого банка заданий ЕГЭ по математике на прямолинейное движение.
Также смотрите видеолекцию «Текстовые задачи» здесь .
Задачи В14 могут встретиться на ЕГЭ по математике совсем простые, где может даже не потребоваться введение переменной. Чаще будут встречаться задачи, сводимые к решению квадратных уравнений (кстати, что делать, если дискриминант намечается слишком большой, – смотрите здесь и здесь).
Задание 1.
Два велосипедиста одновременно отправились в 130-километровый пробег. Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч.
Пусть км/ч – скорость второго велосипедиста. Тогда согласно условию км/ч – скорость первого велосипедиста.
Оба велосипедиста проехали 130 км.
Третью колонку таблицы заполняем автоматически, пользуясь формулой :
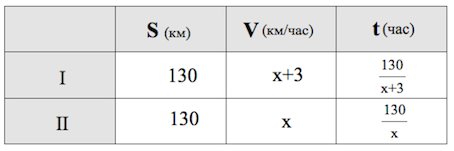
Время движения первого велосипедиста меньше, чем время движения второго на 3 часа, поэтому
Домножаем обе части равенства на , понимая, при этом, что
К финишу придет первым велосипедист со скоростью , поэтому в ответ отправляем величину (км/ч).
Задание 2.
Из пункта А в пункт В, расстояние между которыми 60 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 110 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 5,5 часов позже автомобилиста. Ответ дайте в км/ч.
Задача очень похожа на предыдущую.
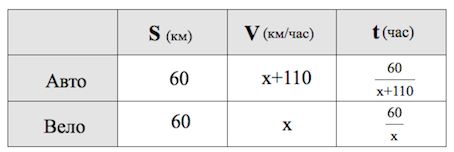
Если не знаете как извлечь корень из большого дискриминанта, загляните сюда и сюда.
Задание 3.
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 80 км. На следующий день он отправился обратно со скоростью на 2 км/ч больше прежней. По дороге он сделал остановку на 2 часа. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
Пусть км/ч – скорость велосипедиста на пути АВ. Тогда согласно условию км/ч – скорость велосипедиста на пути ВА.
Длину пути АВ (ВА) 80 км.
Третью колонку таблицы заполняем автоматически, пользуясь формулой :
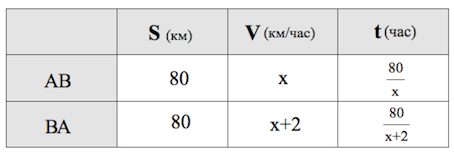
Время движения велосипедиста на пути ВА меньше, чем время движения на пути АВ на 2 часа, поэтому
Откуда вытекает, что (км/ч).
Задание 4.
Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 10 км/ч, а вторую половину пути – со скоростью 60 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 39 км/ч. Ответ дайте в км/ч.
Пусть км/ч – скорость первого автомобиля. Тогда согласно условию км/ч – скорость второго автомобиля на первой половине пути. При этом весь путь считаем км.
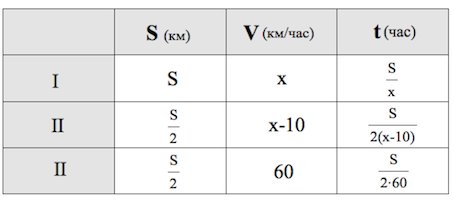
Так как автомобили выехали одновременнно из А и прибыли одновременно в В, то
В условии задачи сказано, что скорость первого автомобиля больше 39 км/ч, поэтому оставляем только вариант
Задание 5.
Из двух городов, расстояние между которыми равно 300 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 70 км/ч и 80 км/ч?
Обозначим за ч время нахождения в пути одного автомобиля до встречи с другим.
Тогда один из автомобилий прошел , второй – км.
В сумме эти пути дают км.
Задание 6.
Из городов A и B, расстояние между которыми равно 300 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 2 часа на расстоянии 160 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч.
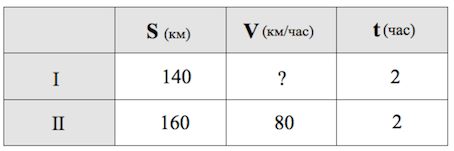
Встреча произошла ближе к А. То есть автомобиль, выехавший из А, проехал меньший путь, нежели автомобиль из В.
Итак, скорость движения автомобиля, выехавшего из А, есть км/ч.
Задание 7.
Расстояние между городами A и B равно 620 км. Из города A в город B выехал первый автомобиль, а через два часа после этого навстречу ему из города B выехал со скоростью 90 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 350 км от города A. Ответ дайте в км/ч.

Второй автомобиль проехал км со скоростью км/ч, значит он находился в пути часа.
Первый автомобиль находился в пути на два часа больше, то есть 5 часов.
Поэтому скорость первого автомобиля, проехавшего км за 5 часов есть км/ч.
Задание 8.
Товарный поезд каждую минуту проезжает на 450 метров меньше, чем скорый, и на путь в 240 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
Прежде всего, переведем м/мин в км/ч.
Обозначаем за км/ч скорость скорого поезда. Тогда скорость товарного – км/ч.
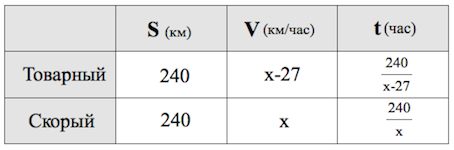
(«Страшные дискриминанты» мы обсуждали здесь)
Откуда Тогда скорость товарного поезда км/ч.
Задание 9.
Расстояние между городами A и B равно 198 км. Из города A в город B выехал автомобиль, а через 3 часа следом за ним со скоростью 80 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.
Пусть расстояние от A до C – км. Так как скорость мотоциклиста км/ч, то время в пути AC мотоциклиста – . По условию сказано, что автомобиль в пути AC находился на 3 часа больше, поэтому указываем в таблице время нахождения автомобиля в пути AC – часов.
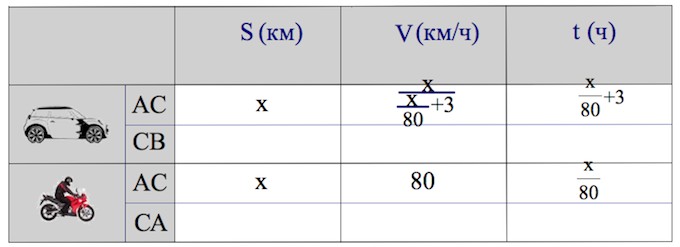
Далее, автомобиль проделывает путь CB, длина которого выражается у нас через , а мотоциклист возвращается обратно, то есть проделывает все тот же путь CA с той же скоростью км/ч за тоже время .
Скорость автомобилиста на пути CB, также как и скорость на пути AC, есть или км/ч.
Поэтому расстояние с этой скоростью он пройдет за время часов.
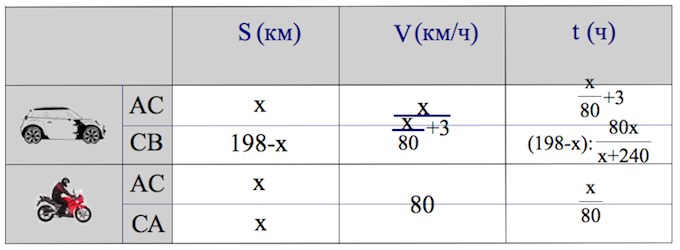
Время прохождения автомобилистом пути CB равно времени прохождения пути CA мотоциклистом, поэтому
Вычисление корня квадратного из большого числа – смотрите здесь.
Задание 10.
Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 475 метрам?
Обозначаем за м/мин скорость второго пешехода и за м – пройденный им путь.
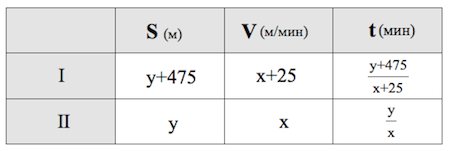
Задание 11.
Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 12 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.
Обозначим за (км/ч) скорость третьего велосипедиста.
Обозначим за (ч) время, прошедшее от старта третьего велосипедиста до встречи со вторым. За это время третий велосипедист проехал км.
Тогда второй находился в пути до встречи с третьим велосипедистом часов и преодолел путь км.
Далее, первый велосипедист, согласно условию, находился в пути часов до встречи второго и третьего велосипедистов и его путь за это время составил
После этого первый, так же как и третий, проехали еще по и км соответственно.
Нам предстоит решить систему:
Конечно же, второй вариант не подходит, так как скорость третьего велосипедиста явно должна быть больше 12 км/ч, иначе он никого не сможет перегнать.
Задание 12.
Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо придорожного столба за 30 секунд. Найдите длину поезда в метрах.
Согласно условию за 30 секунд поезд проходит расстояние, равное своей длине .
Чтобы найти длину поезда , нужно скорость поезда умножить на секунд.
При этом, заметьте, требуется перевод всех данных в один формат.
Задание 13.
Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо лесополосы, длина которой равна 500 метров, за 36 секунд. Найдите длину поезда в метрах.
Согласно условию за 36 минут поезд проходит м, где – длина поезда.
Переведем км/ч в м/мин:
Задание 14.
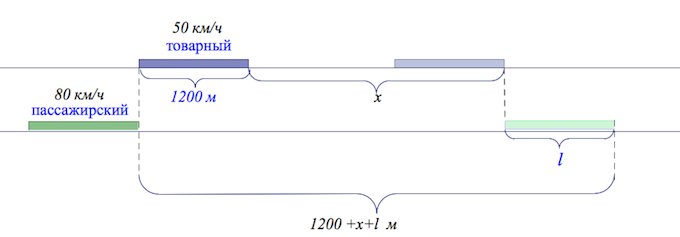
По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 80 км/ч и 50 км/ч. Длина товарного поезда равна 1200 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 3 минутам. Ответ дайте в метрах.
Переведем сразу км/ч в м/мин:
За 3 минуты товарный поезд прошел м:
а пассажирский (м).
Согласно условию пассажирский поезд за 3 минуты прошел путь, равный м.
Смотрите фрагмент видеолекции

Побольше оптимизма! И все будет хорошо!

Вы можете пройти тест по задачам на движение по прямой.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
- Задания №11. Текстовые задачи на среднюю скорость
- Задачи №10, часть 4
- Задачи №10, часть 1
- Задания №11. Задачи на прогрессию
- Задачи №10 , часть 2
- Задачи №10, часть 3
Здравствуйте! В задании 3 у Вас неправильно найдены корни. Ответ должен быть 8.
Источники:
https://velife.ru/katanie/kak-pravilno-i-bezopasno-ezdit-na-velosipede-po-ozhivlennomu-shosse.html
https://novstudent.ru/zadachi-na-dvizhenie/
https://znanio.ru/media/testovye-zadaniya-na-znaniya-osnov-privil-dorozhnogo-dvizheniya-7-9-klassy-2673835
http://spacemath.xyz/zadachi-na-dvizhenie/
https://egemaximum.ru/13-5/
