Скорость велосипеда: средняя, максимальная, рекордная в км/ч

Однако многие задаются вопросом, какую скорость может развить велосипедист в различных условиях? Вне зависимости от причин, мы попробуем ответить на этот вопрос и разобраться с факторами, влияющими на скорость передвижения.
Скоростной тест
Рассмотрим показатели наиболее распространенных типов велосипедов – горный, шоссейный и городской, а также их промежуточных «братьев» — гибрид и туристический велосипед.

Другие типы предназначены не для быстрой езды, поэтому в сравнении не участвуют. Для интереса добавим показатели электровелосипеда. Также читайте обзор ТОПовых производителей велосипедов и не ошибайтесь с выбором.
Результаты:
- электровелосипед – 25-30 км/ч;
- шоссейный – 21-25 км/ч;
- туристический – 20-23 км/ч;
- гибрид – 19-21 км/ч;
- горный – 18-20 км/ч;
- городской – 15-17 км/ч.
Электровелосипед мог бы показать и больший результат, но его скорость езды ограничена контроллером. Для туристических велосипедов, оборудованных вело рюкзаками, оптимальной считается скорость 17 км/ч.
Город
Городские условия езды нивелируют скоростные характеристики разных типов велосипедов из-за необходимости частого маневрирования и преодоления препятствий. Скорость велосипеда в городе – 15-18 км/ч.

Так же интересен тот факт, что в условиях мегаполисов, на дистанциях до 5 км велосипед «быстрее» других видов транспорта. На дистанциях 5-10 км его средняя скорость сопоставима с автомобилем. Плюс у велосипедиста есть возможность двигаться не только по проезжей части, а проложить свой маршрут через парк или дворовые зоны.
Профессионалы
Опытные спортсмены способны преодолевать расстояния в 100 километров, двигаясь со средней скоростью около 30 км/ч. Так Руй Кошта (победитель групповой гонки на 242 км) в 2013 году проехал дистанцию со средней скоростью 36 км/ч.
Для примера приведем нормы получения разрядов велоспорт-шоссе в дисциплине «индивидуальная гонка на время» (РОССИЯ):
| Звание/разряд | Дистанция (км) | Время (минут) | Средняя скорость (км/ч) |
| МСМК мужчины | 50 | 64 | 46,88 |
| МСМК женщины | 25 | 35,5 | 42,25 |
| МС мужчины | 25 | 33 | 45,46 |
| МС женщины | 25 | 37,5 | 40 |
| КМС мужчины | 25 | 35,5 | 42,25 |
| КМС женщины | 25 | 40 | 37,5 |
Немного истории
По нормативам ГТО в СССР, чтобы получить золотой значок, необходимо было проехать на велосипеде:
| Возраст (лет)/пол | Дистанция (км) | Время (минут) | Средняя скорость (км/ч) |
| 19-28 мужчины | 20 | 43 | 27,91 |
| 18-28 женщины | 10 | 25 | 24 |
| 29-39 мужчины | 20 | 46 | 26,09 |
| 29-34 женщины | 10 | 27 | 22,22 |
Факторы, влияющие на скорость велосипеда
Подготовка велосипедиста
Больше всего скорость езды зависит от физической силы и выносливости человека. Второе место занимает техника езды. Пол ездока не оказывает существенного влияния на скорость передвижения.
Сопротивление воздуха
При отсутствии ветра, проблемы сопротивления воздушному потоку начинаются на скоростях в 25-27 км/ч. При встречном ветре трудности движения возникают при скорости 10-15 км/ч. Влияние воздушного потока зависит насколько правильная посадка велосипедиста.

На горном велосипеде, при высокой посадке, увеличивается площадь сопротивления набегающему потоку, и езда замедляется. На шоссейном велосипеде, благодаря узкому рулю с нижним захватом, есть возможность обеспечить туловищу практически горизонтальное положение. Это позволяет облегчить передвижение, благодаря уменьшению площади тела, сопротивляющемуся встречному потоку воздуха.
Сопротивление качению
На твердых поверхностях уменьшить сопротивление качению позволяет меньшая площадь соприкосновения колеса с дорожным полотном. Добиться этого можно, либо сильно накачав широкие покрышки, либо заменить их более узкими.

На мягких поверхностях (грунт или песок) все происходит наоборот. Широкие, или немного спущенные покрышки имеют приоритет перед узкими.
Размер колеса тоже имеет далеко не последнее значение. Велосипед с широкими колесами дольше сохраняет силу инерции и легче преодолевает неровности дорожного покрытия, что положительно сказывается на скорости езды.
Силы трения
На скорости велосипеда отражается техническое состояние его трущихся деталей. Цепь и втулки необходимо содержать в хорошо смазанном состоянии и не допускать их загрязнения. Слишком мягкие амортизаторы снижают скорость, но добавляют комфорта при движении по неровным поверхностям.
Надеемся, что информация данной статьи поможет вам оптимально выбрать и настроить велосипед под свои условия передвижения. Желаем вам хороших скоростей и удовольствия от езды.
Задачи на движение для 4 класса — формулы и примеры решений
Существует несколько типов задач на движение. Примеры решения всех типов задач с пояснениями мы рассмотрим в этой статье.
Задачи на движение в одном направлении
Задачи на движении в одном направлении относятся к одному из трех основных видов задач на движение.
Если два объекта выехали из одного пункта одновременно, то, поскольку они имеют разные скорости, объекты удаляются друг от друга. Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:
Если из одного пункта выехал один объект, а спустя некоторое время в том же направлении вслед за ним выехал другой объект, то они могут как сближаться, так и удаляться друг от друга.
Если скорость объекта, движущегося впереди, меньше движущегося вслед за ним объекта, то второй догоняет первого и они сближаются.
Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:
Если скорость объекта, который идет впереди, больше скорости объекта, который движется следом, то второй не сможет догнать первого и они удаляются друг от друга.
Скорость удаления находим аналогично — из большей скорости вычитаем меньшую:
Задачи на скорость сближения
Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?
Решение :
Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалится от города на:
Второй автомобиль движется быстрее первого, значит каждый час расстояние между автомобилями будет сокращаться на разность их скоростей:
60 — 40 = 20 (км/ч) – это скорость сближения автомобилей
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся:
Решение задачи по действиям можно записать так:
1) 40 · 4 = 160 (км) – расстояние между автомобилями
2) 60 — 40 = 20 (км/ч) – скорость сближения автомобилей
Ответ: Второй автомобиль догонит первый через 8 часов.
Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов:
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого:
Решение задачи по действиям можно записать так:
1) 5 — 4 = 1 (км/ч) – это скорость сближения пешеходов
Ответ: Через 5 часов второй пешеход догонит первого.
Из одного села в одном направлении одновременно выехали два велосипедиста. Скорость одного из них — 15 км/ч, скорость другого — 12 км/ч. Какое расстояние будет через ними через 4 часа?

Решение:
1) 15-12=3 (км/ч) скорость удаления велосипедистов
2) 3∙4=12 (км) такое расстояние будет между велосипедистами через 4 часа.
Ответ: Через 4 часа расстояние между велосипедистами составит 12 км.
Задача 4
Из села на станцию одновременно вышел пешеход и выехал велосипедист. Через 2 часа велосипедист опережал пешехода на 12 км. Найти скорость пешехода, если скорость велосипедиста 10 км/ч.

Решение:
1) 12:2=6 (км/ч) скорость удаления велосипедиста и пешехода
2) 10-6=4 (км/ч) скорость пешехода.
Ответ: Скорость пешехода составляет 4 км/ч.
Задачи на скорость удаления
Задача 1
Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.
Решение:
Сначала узнаем скорость удаления автомобилей друг от друга, для этого вычтем из большей скорости меньшую:
Каждый час автомобили отдаляются друг от друга на 40 км. Теперь можно узнать сколько километров будет между ними через 3 часа, для этого скорость удаления умножим на 3:
Чтобы узнать через сколько часов расстояние между автомобилями станет 200 км, надо расстояние разделить на скорость удаления:
Ответ:
Если два объекта движутся навстречу друг другу, то они сближаются. Чтобы найти скорость сближения двух объектов, движущихся навстречу друг другу, надо сложить их скорости:
Скорость сближения больше, чем скорость каждого из них.
Из поселка и города навстречу друг другу, одновременно выехали два автобуса. Один автобус до встречи проехал 100 км со скоростью 25 км/час. Сколько километров до встречи проехал второй автобус, если его скорость 50 км/час.
1) 100 : 25 = 4 (часа ехал один автобус)
2) 50 * 4 = 200
Решение в виде выражения: 50 * (100 : 25) = 200
Ответ: второй автобус проехал до встречи 200 км.
Расстояние между двумя пристанями 90 км. От каждой из них одновременно навстречу друг другу вышли два теплохода. Сколько часов им понадобится чтобы встретиться, если скорость первого 20 км/час, а второго 25 км/час?
1) 25 + 20 = 45 (сумма скоростей теплоходов)
Решение в виде выражения:90 : (20 + 25) = 2
Ответ: Теплоходы встретятся через 2 часа.
От двух станций, расстояние между которыми 564 км., одновременно навстречу друг другу вышли два поезда. Скорость одного из них 63 км/час. Какова скорость второго, если поезда встретились через 4 часа?
1) 63 * 4 = 252 (прошел 1 поезд)
2) 564 — 252 =312 (прошел 2 поезд)
Решение в виде выражения (63 * 4 — 252) : 4 = 78
Ответ: Скорость второго поезда 78 км/час.
Задача 4
Два велосипедиста выехали навстречу друг другу. Скорость одного из низ 12 км/ч, а другого — 10 км/ч. Через 3 часа они встретились. Какое расстояние было между ними в начале пути?
Решение:
1) 12+10=22 (км/ч) скорость сближения велосипедистов
2) 22∙3=66 (км) было между велосипедистами в начале пути.
Ответ: Расстояние между велосипедистами в начале пути было 66 км.
Два поезда идут навстречу друг другу. Скорость одного из них 50 км/ч, скорость другого — 60 км/ч. Сейчас между ними 440 км. Через сколько часов они встретятся?
Решение:
1) 60+50=110 (км/ч) скорость сближения поездов
2) 440:110=4 (ч) время, через которое поезда встретятся.
Ответ: Поезда встретятся через 4 часа.
Движение в противоположных направлениях
Если два объекта движутся в противоположных направлениях, то они удаляются. Чтобы найти скорость удаления, надо сложить скорости этих объектов:
Скорость удаления больше скорости любого из них.
Из поселка вышли одновременно в противоположных направлениях два пешехода. Средняя скорость одного пешехода – 5 км/ч, другого – 4 км/ч. Через сколько часов расстояние между ними будет 27 км ?
Чтобы найти время движения пешеходов, нужно знать расстояние и скорость пешеходов. Мы знаем, что за каждый час один пешеход удаляется от поселка на 5 км, а другой пешеход удаляется от поселка на 4 км. Можем найти их скорость удаления.
1. (км/ч)
Мы знаем скорость удаления и знаем все расстояние – 27 км. Можем найти время, через которое пешеходы удалятся друг от друга на 27 км, для этого нужно расстояние разделить на скорость.
2. (ч)
Ответ: Через три часа расстояние между переходами будет 27 км.
Из поселка вышли одновременно в противоположных направлениях два пешехода. Через 3 часа расстояние между ними было 27 км. Первый пешеход шел со скоростью 5 км/ч. С какой скоростью шел второй пешеход ?
Чтобы узнать скорость второго пешехода, надо знать расстояние, которое он прошел, и его время в пути. Чтобы узнать, какое расстояние прошел второй пешеход, надо знать, какое расстояние прошел первый пешеход и общее расстояние. Общее расстояние мы знаем. Чтобы найти расстояние, которое прошел первый пешеход, надо знать его скорость и его время в пути. Средняя скорость движения первого пешехода – 5 км/ч, его время в пути – 3 часа. Если среднюю скорость умножить на время в пути, получим расстояние, которое прошел пешеход:
1. (км)
Мы знаем общее расстояние и знаем расстояние, которое прошел первый пешеход. Можем теперь узнать, какое расстояние прошел второй пешеход.
2. (км)
Теперь мы знаем расстояние, которое прошел второй пешеход, и время, проведенное им в пути. Можем найти его скорость.
3. (км/ч)
Ответ: Скорость второго пешехода – 4 км/ч.
Товарный и пассажирский поезда движутся в противоположных направлениях. Скорость товарного 45 км/ч, скорость пассажирского — 70 км/ч. Сейчас между ними 20 км. Какое расстояние будет между ними через 2 часа ?

1) 70+45=115 (км/ч) скорость удаления поездов
2) 115∙2=230 (км) пройдут поезда вместе за 2 часа
3) 230+20=250 (км) такое расстояние между поездами будет через 2 часа.
Ответ: Через 2 часа расстояние между поездами составит 250 км.
Из одного пункта одновременно в противоположных направлениях выехали два мотоциклиста. Скорость одного из них — 60 км/ч, скорость другого — 40 км/ч. Через какое время расстояние между ними станет равным 300 км?

1) 60+40=100 (км/ч) скорость удаления мотоциклистов
2) 300:100=3 (ч) через такое время расстояние между ними будет 300 км.
Ответ: Расстояние между мотоциклистами станет 300 км через 3 часа.
Задачи на движение
Задачи на движение начинают проходить в 5 классе и решают все оставшиеся учебные годы вплоть до 11 класса. В ЕГЭ по математике вы найдете задачи на движение в задании 11, в котором собраны все текстовые задачи. Рассмотрим как надо решать задачи на движение из ЕГЭ. Но сначала немного теории.
Как решать задачи на движение
Решение задач на движение подчиняется четкому алгоритму, который состоит из нескольких этапов:
- Анализ данных.
- Составление таблицы.
- Составление уравнения.
- Решение уравнения.
Остановимся подробно на каждом пункте:
1. Первое, с чего нужно начать — медленно и вдумчиво прочитать условие задачи, то есть проанализировать данные.
Чтобы наглядно представить задачу, необходимо сделать рисунок и отобразить на нем все известные по условию задачи величины.
2. Второй шаг — составить таблицу по условию задачи, внести в таблицу известные величины и ввести неизвестные.
Таблица состоит из трех столбцов S, v и t (путь, скорость и время) и нескольких строк. При заполнении каждой строки сначала выбираем и заполняем тот столбец, информация о котором дана в задаче. Еще один столбец записываем в роли неизвестного (чаще всего, это то, что требуется найти в задаче). В третью, оставшуюся колонку вписываем связь характеристик из двух уже заполненных столбцов по формуле:
В таблице получается столько строчек, сколько каждый из объектов задачи действовал (то есть, перемещался) или мог бы действовать.
3. Следующий шаг — при помощи сделанного рисунка и заполненной таблицы составить уравнение или систему уравнений.
По окончании заполнения таблицы оказывается, что есть часть информации, которая не вошла в таблицу. Эта информация характеризует те значения величин в колонках, которые вычисляются в третью очередь, то есть по формуле. На основании этой информации и данных из третьей колонки составляем уравнение.
4. Решить полученное уравнение и прийти к ответу.
Когда уравнение составлено, последний шаг — это решить его, и, в конце концов, получить ответ.
Будьте внимательны, если за неизвестное вы приняли не то, что требуется найти в задаче. В этом случае следует выразить то, что нужно найти через полученное решение уравнения.
Если, решив уравнение, вы получили несколько ответов, то следует отобрать только имеющие смысл решения. Помните, что путь, скорость и время не могут быть отрицательными.
Примеры решения
Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.
В задаче требуется найти скорость второго, более медленного, велосипедиста. Примем его скорость за x. Заполним таблицу:
| v, км/ч | t, ч | S, км | |
| Первый велосипедист | x + 10 | 60 | |
| Второй велосипедист | x | 60 |
В условии задачи сказано, что первый велосипедист прибыл к финишу на 3 часа раньше второго. На основании этого составим уравнение:
Получаем два корня, x1 = 10 и x2 = –20. Второй корень не подходит, так как скорость не может быть отрицательной.
Виды задач на движение
Если два объекта движутся навстречу друг другу, то они сближаются:
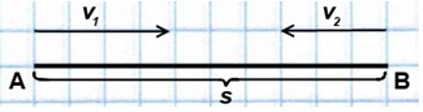
При движении в противоположном направлении объекты удаляются:
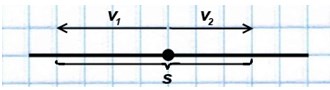
В обоих случаях объекты как бы «помогают» друг другу преодолеть общее для них расстояние, «действуют сообща». Поэтому чтобы найти их совместную скорость (это и будет скорость сближения или удаления), нужно складывать скорости объектов:
Движение друг за другом (вдогонку)
При движении в одном направлении объекты также могут как сближаться, так и удаляться. В этом случае они как бы «соревнуются» в преодолении общего расстояния, «действуют друг против друга». Поэтому их совместная скорость будет равна разности скоростей.
Если скорость идущего впереди объекта меньше скорости объекта, следующего за ним, то они сближаются. Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:
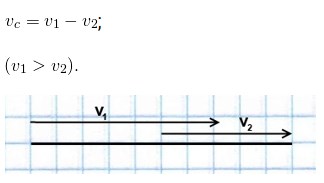
Если объект, идущий впереди, движется с большей скоростью, чем идущий следом за ним, то они удаляются. Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:
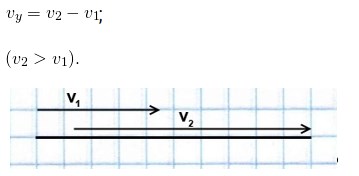
При движении навстречу друг другу и движении в противоположных направлениях скорости складываем.
При движении в одном направлении скорости вычитаем.
Задачи на движение по кругу
При движении по кругу объекты могут:
- сближаться, если скорость догоняющего больше скорости догоняемого. Скорость сближения будет равна ;
- отдаляться, если скорость догоняющего меньше скорости догоняемого. Скорость удаления будет равна .
При этом пройденные расстояния измеряются длиной круговой трассы, равной S.
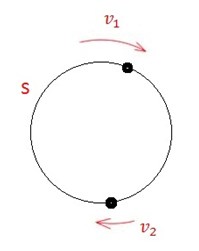
- Если два объекта начинают движение по кругу из одной и той же точки, то в момент первой встречи более быстрый объект пройдет расстояние на один круг больше.
- Если два объекта начинают движение по кругу из разных точек, расстояние между которыми равно S0, то в момент первой встречи догоняющий объект пройдет на S0 км большее расстояние, чем догоняемый.
- Если через определенное время t первый объект опережает второй на m кругов, то разница пройденных объектами расстояний будет равна m · S: S1 – S2 = m · S.
Задачи на движение мимо объекта
В задачах на движение мимо объекта обязательно присутствуют протяженные тела — поезда, туннели, корабли и т. п. Зачастую движущимся объектом является поезд.
Если поезд длиной L движется мимо точечного объекта (столба, светофора, человека), то он проходит расстояние, равное его длине L:
При этом, если точечный объект (пешеход, велосипедист) тоже движется, то совместная скорость равна сумме скоростей, если поезд и объект двигаются в разных направлениях (как в пункте 1), и равна разности скоростей, если они двигаются в одном направлении (как в пункте 2).
Если поезд длиной L1 движется мимо протяженного объекта (туннеля, лесополосы) длиной L2, то он проходит расстояние, равное сумме длин самого поезда и протяженного объекта:
S = L1 + L2 = v0 · t.
При этом, если протяженный объект (например, другой поезд) тоже движется, то совместная скорость равна сумме скоростей, если оба объекта двигаются в разных направлениях, и равна разности скоростей (из большей вычитается меньшая), если они двигаются в одном направлении.
Задачи на движение по течению и против течения
В задачах на движение помимо собственной скорости плывущего тела нужно учитывать скорость течения.
При движении по течению скорость течения прибавляется к скорости плывущего тела: v = v0 + vтеч.
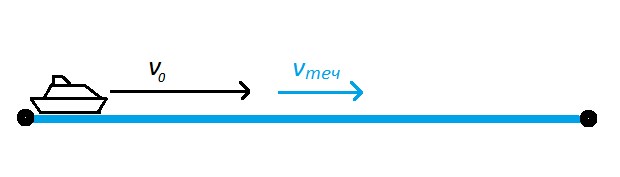
При движении против течения скорость течения отнимается от скорости плывущего тела: v = v0 – vтеч.

Задачи на движение из ЕГЭ по математике (профильный уровень)
Задача 1.
Из одной точки круговой трассы, длина которой равна 44 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 112 км/ч, и через 48 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение: Пусть скорость второго автомобиля равна v км/ч. За 4/5 часа первый автомобиль прошел на 44 км больше, чем второй, отсюда имеем:
112 ∙ alt=»\frac{4}{5}» width=»7″ height=»22″ />= v ∙ alt=»\frac{4}{5}» width=»7″ height=»22″ />+ 44 ⇔ 4 ∙ v = 112 ∙ 4 – 44 ∙ 5 ⇔ v = 57.
Следовательно, скорость второго автомобиля была равна 57 км/ч.
Ответ: 57 км/ч.
Задача 2.
Из пункта A круговой трассы выехал велосипедист, а через 10 минут следом за ним отправился мотоциклист. Через 2 минуты после отправления он догнал велосипедиста в первый раз, а еще через 3 минуты после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 5 км. Ответ дайте в км/ч.
Решение:
До первой встречи велосипедист провел на трассе 1/5 часа, а мотоциклист 1/30 часа. Пусть скорость мотоциклиста равна v км/ч, тогда скорость велосипедиста равна
Тогда если скорость велосипедиста – это 1 единица отношения, то скорость мотоциклиста – это 6 единиц отношения.
Так как они едут в одном направлении, их общая скорость 5 единиц отношения.
∙5 ед.отн. = 5
Таким образом, скорость мотоциклиста была равна 120 км/ч.
Ответ: 120 км/ч.
Задача 3
Часы со стрелками показывают 3 часа ровно. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?
Решение: Скорость движения минутной стрелки 12 делений/час (под одним делением здесь подразумевается расстояние между соседними цифрами на циферблате часов), а часовой ― 1 деление/час. До девятой встречи минутной и часовой стрелок минутная должна сначала 8 раз «обогнать» часовую, то есть пройти 8 кругов по 12 делений. Пусть после этого до четвертой встречи часовая стрелка пройдет L делений. Тогда общий путь минутной стрелки складывается из найденных 96 делений, ещё 3 изначально разделяющих их делений (поскольку часы показывают 3 часа) и последних L делений. Приравняем время движения для часовой и минутной стрелок:
, отсюда и .
Ответ: через 9 минут.
Задача 4
Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение:
Данную задачу можно интерпретировать (представить её, как задачу на линейное движение): Два автомобиля одновременно начинают движение в одном направлении. Скорость первого равна 80 км/ч. Через 40 минут он опережает второго на 14 км (т. к. сказано, что на один круг). Найти скорость второго. Очень важно в заданиях на движение представить сам процесс этого движения.
Сравнение так же производим по расстоянию.
За x принимаем искомую величину ― скорость второго. Время движения 40 минут (2/3 часа) для обоих. Заполним графу «расстояние»:
| v | t | S | |
| 1 | 80 | 2/3 | |
| 2 | x | 2/3 |
Расстояние, пройденное первым, больше расстояния, который прошёл второй на 14 км.
80 ∙ alt=»\frac{2}{3}» width=»7″ height=»22″ />больше, чем x ∙ alt=»\frac{2}{3}» width=»7″ height=»22″ />на 14.
80 ∙ alt=»\frac{2}{3}» width=»7″ height=»22″ />= x ∙ alt=»\frac{2}{3}» width=»7″ height=»22″ />+ 14;
– = x ∙ ;
Скорость второго автомобиля 59 (км/ч).
Ответ: 59 км/ч.
Задача 5
Из пункта A в пункт B, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 6 часов позже автомобилиста. Ответ дайте в км/ч.
Решение:
Пусть v км/ч – скорость велосипедиста, тогда скорость автомобилиста равна v + 40 км/ч. Велосипедист был в пути на 6 часов больше, отсюда имеем:
Задания №11. Задачи на движение по прямой

На этот раз рассматриваем задачи из открытого банка заданий ЕГЭ по математике на прямолинейное движение.
Также смотрите видеолекцию «Текстовые задачи» здесь .
Задачи В14 могут встретиться на ЕГЭ по математике совсем простые, где может даже не потребоваться введение переменной. Чаще будут встречаться задачи, сводимые к решению квадратных уравнений (кстати, что делать, если дискриминант намечается слишком большой, – смотрите здесь и здесь).
Задание 1.
Два велосипедиста одновременно отправились в 130-километровый пробег. Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч.
Пусть км/ч – скорость второго велосипедиста. Тогда согласно условию км/ч – скорость первого велосипедиста.
Оба велосипедиста проехали 130 км.
Третью колонку таблицы заполняем автоматически, пользуясь формулой :
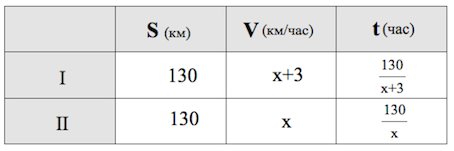
Время движения первого велосипедиста меньше, чем время движения второго на 3 часа, поэтому
Домножаем обе части равенства на , понимая, при этом, что
К финишу придет первым велосипедист со скоростью , поэтому в ответ отправляем величину (км/ч).
Задание 2.
Из пункта А в пункт В, расстояние между которыми 60 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 110 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 5,5 часов позже автомобилиста. Ответ дайте в км/ч.
Задача очень похожа на предыдущую.
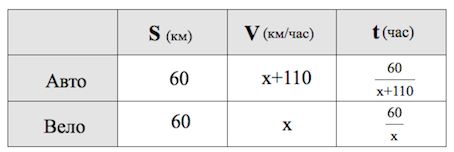
Если не знаете как извлечь корень из большого дискриминанта, загляните сюда и сюда.
Задание 3.
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 80 км. На следующий день он отправился обратно со скоростью на 2 км/ч больше прежней. По дороге он сделал остановку на 2 часа. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
Пусть км/ч – скорость велосипедиста на пути АВ. Тогда согласно условию км/ч – скорость велосипедиста на пути ВА.
Длину пути АВ (ВА) 80 км.
Третью колонку таблицы заполняем автоматически, пользуясь формулой :
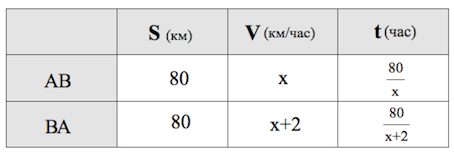
Время движения велосипедиста на пути ВА меньше, чем время движения на пути АВ на 2 часа, поэтому
Откуда вытекает, что (км/ч).
Задание 4.
Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 10 км/ч, а вторую половину пути – со скоростью 60 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 39 км/ч. Ответ дайте в км/ч.
Пусть км/ч – скорость первого автомобиля. Тогда согласно условию км/ч – скорость второго автомобиля на первой половине пути. При этом весь путь считаем км.
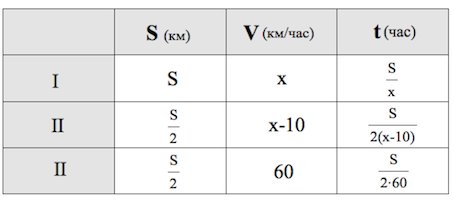
Так как автомобили выехали одновременнно из А и прибыли одновременно в В, то
В условии задачи сказано, что скорость первого автомобиля больше 39 км/ч, поэтому оставляем только вариант
Задание 5.
Из двух городов, расстояние между которыми равно 300 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 70 км/ч и 80 км/ч?
Обозначим за ч время нахождения в пути одного автомобиля до встречи с другим.
Тогда один из автомобилий прошел , второй – км.
В сумме эти пути дают км.
Задание 6.
Из городов A и B, расстояние между которыми равно 300 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 2 часа на расстоянии 160 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч.
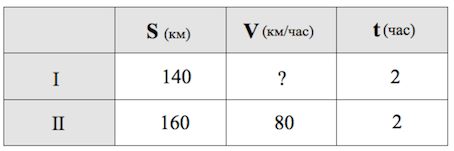
Встреча произошла ближе к А. То есть автомобиль, выехавший из А, проехал меньший путь, нежели автомобиль из В.
Итак, скорость движения автомобиля, выехавшего из А, есть км/ч.
Задание 7.
Расстояние между городами A и B равно 620 км. Из города A в город B выехал первый автомобиль, а через два часа после этого навстречу ему из города B выехал со скоростью 90 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 350 км от города A. Ответ дайте в км/ч.

Второй автомобиль проехал км со скоростью км/ч, значит он находился в пути часа.
Первый автомобиль находился в пути на два часа больше, то есть 5 часов.
Поэтому скорость первого автомобиля, проехавшего км за 5 часов есть км/ч.
Задание 8.
Товарный поезд каждую минуту проезжает на 450 метров меньше, чем скорый, и на путь в 240 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
Прежде всего, переведем м/мин в км/ч.
Обозначаем за км/ч скорость скорого поезда. Тогда скорость товарного – км/ч.
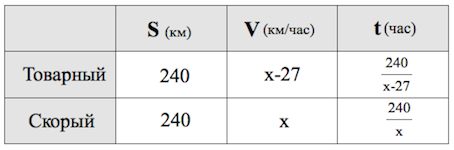
(«Страшные дискриминанты» мы обсуждали здесь)
Откуда Тогда скорость товарного поезда км/ч.
Задание 9.
Расстояние между городами A и B равно 198 км. Из города A в город B выехал автомобиль, а через 3 часа следом за ним со скоростью 80 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.
Пусть расстояние от A до C – км. Так как скорость мотоциклиста км/ч, то время в пути AC мотоциклиста – . По условию сказано, что автомобиль в пути AC находился на 3 часа больше, поэтому указываем в таблице время нахождения автомобиля в пути AC – часов.
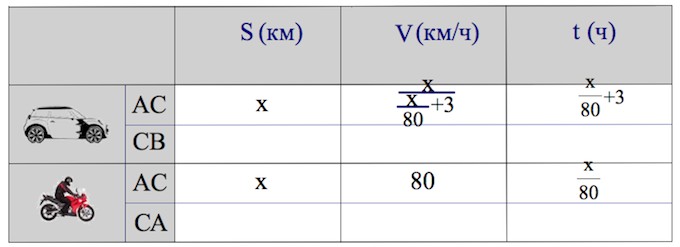
Далее, автомобиль проделывает путь CB, длина которого выражается у нас через , а мотоциклист возвращается обратно, то есть проделывает все тот же путь CA с той же скоростью км/ч за тоже время .
Скорость автомобилиста на пути CB, также как и скорость на пути AC, есть или км/ч.
Поэтому расстояние с этой скоростью он пройдет за время часов.
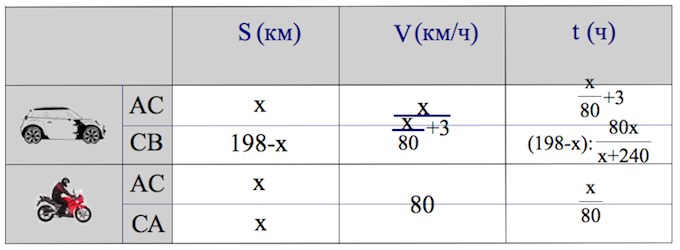
Время прохождения автомобилистом пути CB равно времени прохождения пути CA мотоциклистом, поэтому
Вычисление корня квадратного из большого числа – смотрите здесь.
Задание 10.
Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 475 метрам?
Обозначаем за м/мин скорость второго пешехода и за м – пройденный им путь.
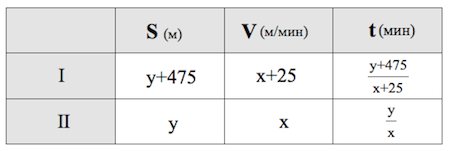
Задание 11.
Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 12 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.
Обозначим за (км/ч) скорость третьего велосипедиста.
Обозначим за (ч) время, прошедшее от старта третьего велосипедиста до встречи со вторым. За это время третий велосипедист проехал км.
Тогда второй находился в пути до встречи с третьим велосипедистом часов и преодолел путь км.
Далее, первый велосипедист, согласно условию, находился в пути часов до встречи второго и третьего велосипедистов и его путь за это время составил
После этого первый, так же как и третий, проехали еще по и км соответственно.
Нам предстоит решить систему:
Конечно же, второй вариант не подходит, так как скорость третьего велосипедиста явно должна быть больше 12 км/ч, иначе он никого не сможет перегнать.
Задание 12.
Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо придорожного столба за 30 секунд. Найдите длину поезда в метрах.
Согласно условию за 30 секунд поезд проходит расстояние, равное своей длине .
Чтобы найти длину поезда , нужно скорость поезда умножить на секунд.
При этом, заметьте, требуется перевод всех данных в один формат.
Задание 13.
Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо лесополосы, длина которой равна 500 метров, за 36 секунд. Найдите длину поезда в метрах.
Согласно условию за 36 минут поезд проходит м, где – длина поезда.
Переведем км/ч в м/мин:
Задание 14.
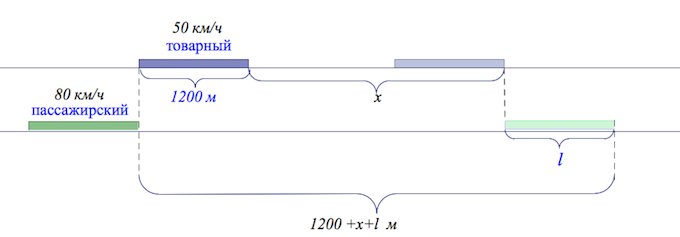
По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 80 км/ч и 50 км/ч. Длина товарного поезда равна 1200 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 3 минутам. Ответ дайте в метрах.
Переведем сразу км/ч в м/мин:
За 3 минуты товарный поезд прошел м:
а пассажирский (м).
Согласно условию пассажирский поезд за 3 минуты прошел путь, равный м.
Смотрите фрагмент видеолекции

Побольше оптимизма! И все будет хорошо!

Вы можете пройти тест по задачам на движение по прямой.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
- Задания №11. Текстовые задачи на среднюю скорость
- Тест по Задачам №11. Задачи на движение
- Задания №11. Задачи на движение по воде
- Задачи №10, часть 1
- Задачи №10, часть 3
- Задания №11. Задачи на прогрессию
Здравствуйте! В задании 3 у Вас неправильно найдены корни. Ответ должен быть 8.
Контрольная работа по физике Кинематика 9 класс
Контрольная работа по физике Кинематика Законы взаимодействия и движения тел 9 класс с ответами. Работа состоит из 4 вариантов в каждом варианте по 9 заданий.
1 вариант
1. Исследуется перемещение слона и мухи. Модель материальной точки может использоваться для описания движения
1) только слона
2) только мухи
3) и слона, и мухи в разных исследованиях
4) ни слона, ни мухи, поскольку это живые существа
2. Вертолёт Ми-8 достигает скорости 250 км/ч. Какое время он затратит на перелёт между двумя населёнными пунктами, расположенными на расстоянии 100 км?
1) 0,25 с
2) 0,4 с
3) 2,5 с
4) 1440 с
3. На рисунках представлены графики зависимости координаты от времени для четырёх тел, движущихся вдоль оси ОХ. Какое из тел движется с наибольшей по модулю скоростью?
4. Велосипедист съезжает с горки, двигаясь прямолинейно и равноускоренно. За время спуска скорость велосипедиста увеличилась на 10 м/с. Ускорение велосипедиста 0,5 м/с 2 . Сколько времени длится спуск?
1) 0,05 с
2) 2 с
3) 5 с
4) 20 с
5. Лыжник съехал с горки за 6 с, двигаясь с постоянным ускорением 0,5 м/с 2 . Определите длину горки, если известно, что в начале спуска скорость лыжника была равна 18 км/ч.
1) 39 м
2) 108 м
3) 117 м
4) 300 м
6. Моторная лодка движется по течению реки со скоростью 5 м/с относительно берега, а в стоячей воде — со скоростью 3 м/с. Чему равна скорость течения реки?
1) 1 м/с
2) 1,5 м/с
3) 2 м/с
4) 3,5 м/с
7. Установите соответствие между физическими величинами и формулами, по которым эти величины определяются.
А) Ускорение
Б) Скорость при равномерном прямолинейном движении
В) Проекция перемещения при равноускоренном прямолинейном движении
8. На пути 60 м скорость тела уменьшилась в 3 раза за 20 с. Определите скорость тела в конце пути, считая ускорение постоянным.
9. Из населённых пунктов А и В, расположенных вдоль шоссе на расстоянии 3 км друг от друга, в одном направлении одновременно начали движение велосипедист и пешеход. Велосипедист движется из пункта А со скоростью 15 км/ч, а пешеход со скоростью 5 км/ч. Определите, на каком расстоянии от пункта А велосипедист догонит пешехода.
2 вариант
1. Два тела, брошенные с поверхности земли вертикально вверх, достигли высот 10 м и 20 м и упали на землю. Пути, пройденные этими телами, отличаются на
1) 5 м
2) 20 м
3) 10м
4) 30 м
2. За 6 минут равномерного движения мотоциклист проехал 3,6 км. Скорость мотоциклиста равна
1) 0,6 м/с
2) 10 м/с
3) 15 м/с
4) 600 м/с
3. На рисунках представлены графики зависимости проекции перемещения от времени для четырёх тел. Какое из тел движется с наибольшей по модулю скоростью?
4. Во время подъёма в гору скорость велосипедиста, двигающегося прямолинейно и равноускоренно, изменилась за 8 с от 18 км/ч до 10,8 км/ч. При этом ускорение велосипедиста было равно
1) -0,25 м/с 2
2) 0,25 м/с 2
3) -0,9 м/с 2
4) 0,9 м/с 2
5. Аварийное торможение автомобиля происходило в течение 4 с. Определите, каким был тормозной путь, если начальная скорость автомобиля 90 км/ч.
1) 22,5 м
2) 45 м
3) 50 м
4) 360 м
6. Пловец плывёт по течению реки. Определите скорость пловца относительно берега, если скорость пловца относительно воды 0,4 м/с, а скорость течения реки 0,3 м/с.
1) 0,5 м/с
2) 0,1 м/с
3) 0,5 м/с
4) 0,7 м/с
7. Установите соответствие между физическими величинами и их единицами измерения в СИ.
А) скорость
Б) ускорение
В) время
Единицы измерения СИ
1) мин
2) км/ч
3) м/с
4) с
5) м/с 2
8. Поезд начинает равноускоренное движение из состояния покоя и проходит за четвёртую секунду 7 м. Какой путь пройдёт тело за первые 10 с?
9. Катер, переправляясь через реку шириной 800 м, двигался перпендикулярно течению реки со скоростью 4 м/с в системе отсчёта, связанной с водой. На сколько будет снесён катер течением, если скорость течения реки 1,5 м/с?
3 вариант
1. Решаются две задачи:
А: рассчитывается маневр стыковки двух космических кораблей;
Б: рассчитываются периоды обращения космических кораблей вокруг Земли.
В каком случае космические корабли можно рассматривать как материальные точки?
1) Только А
2) Только Б
3) И А, и Б
4) Ни А, ни Б
2. Средняя скорость поезда метрополитена 40 м/ с. Время движения между двумя станциями 4 минуты. Определите, на каком расстоянии находятся эти станции.
1) 160 м
2) 1000 м
3) 1600 м
4) 9600 м
3. На рисунках представлены графики зависимости проекции скорости от времени для четырёх тел, движущихся вдоль оси ОХ. Какое из тел движется с постоянной скоростью?

4. Ускорение велосипедиста на одном из спусков трассы равно 1,2 м/с 2 На этом спуске его скорость увеличилась на 18 м/с. Велосипедист спускается с горки за
1) 0,07 с
2) 7,5 с
3) 15 с
4) 21,6 с
5. Какое расстояние пройдёт автомобиль до полной остановки, если шофёр резко тормозит при скорости 72 км/ч, а от начала торможения до остановки проходит 6 с?
1) 36 м
2) 60 м
3) 216 м
4) 432 м
6. Катер движется по течению реки со скоростью 11 м/с относительно берега, а в стоячей воде — со скоростью 8 м/с. Чему равна скорость течения реки?
1) 1 м/с
2) 1,5 м/с
3) 3 м/с
4) 13 м/с
7. Установите соответствие между физическими величинами и формулами, по которым эти величины определяются.
А) Проекция ускорения
Б) Проекция перемещения при равномерном прямолинейном движении
В) Проекция скорости при равноускоренном прямолинейном движении
8. Скорость материальной точки на пути 60 м увеличилась в 5 раз за 10 с. Определить ускорение, считая его постоянным.
9. Товарный поезд едет со скоростью 36 км/ч. Спустя 30 минут с той же станции по тому же направлению выходит экспресс со скоростью 144 км/ч. На каком расстоянии от станции экспресс догонит товарный поезд?
4 вариант
1. Два тела, брошенные с поверхности земли вертикально вверх, достигли высот 10 м и 20 м и упали на землю. Перемещения этих тел соответственно равны
1) 10 м, 20 м
2) 20 м, 40 м
3) Ом, Ом
4) Ом, 20 м
2. Велосипедист, двигаясь равномерно по шоссе, проехал 1800 м за 3 минуты. Скорость велосипедиста равна
1) 12 км/ч
2) 24 км/ч
3) 36 км/ч
4) 60 км/ч
3. На рисунках представлены графики зависимости модуля ускорения от времени для разных видов движения. Какой график соответствует равномерному движению?

4. Санки съехали с одной горки и въехали на другую. Во время подъёма на горку скорость санок, двигавшихся прямолинейно и равноускоренно, за 4 с изменилась от 12 м/с до 2 м/с, при этом модуль ускорения был равен
1) -2,5 м/с 2
2) 2,5 м/с 2
3) -3,5 м/с 2
4) 3,5 м/с 2
5. При равноускоренном прямолинейном движении скорость катера увеличилась за 10 с от 5 м/с до 9 м/с. Какой путь пройден катером за это время?
1) 50 м
2) 70 м
3) 80 м
4) 90 м
6. Пловец плывёт против течения реки. Определите скорость пловца относительно берега, если скорость пловца относительно воды 0,4 м/с, а скорость течения реки 0,3 м/с.
1) 0,1 м/с
2) 0,2 м/с
3) 0,5 м/с
4) 0,7 м/с
7. Установите соответствие между физическими величинами и их единицами измерения в СИ.
А) перемещение
Б) скорость
В) время
Единицы измерения СИ
8. Тело, двигаясь равноускоренно, в течение пятой секунды от начала движения прошло путь 45 м. Какой путь оно пройдёт за 8 с от начала движения?
9. Пловец пересекает реку шириной 240 м. Скорость течения реки 1,2 м/с. Скорость пловца относительно воды 1,5 м/с и направлена перпендикулярно к вектору течения. На сколько метров пловец будет снесён течением к тому моменту, когда он достигнет противоположного берега?
Ответы на контрольную работу по физике Кинематика
1 вариант
1-3, 2-4, 3-4, 4-4, 5-1, 6-3, 7-425, 8-1,5 м/с, 9-4,5 км
2 вариант
1-2, 2-2, 3-3, 4-1, 5-3, 6-4, 7-354, 8-100 м, 9-300 м
3 вариант
1-2, 2-4, 3-1, 4-3, 5-2, 6-3, 7-431, 8-0,8 м/с 2 , 9-24 км
4 вариант
1-3, 2-3, 3-4, 4-2, 5-2, 6-1, 7-534, 8-320 м, 9-192 м
Источники:
https://zextrem.com/zemlya/velosport/srednyaya-skorost-velosipeda.html
https://sprint-olympic.ru/uroki/matematika-uroki/93258-zadachi-na-dvijenie-dlia-4-klassa-formyly-i-primery-reshenii.html
https://novstudent.ru/zadachi-na-dvizhenie/
https://egemaximum.ru/13-5/
https://testschool.ru/2017/07/27/kontrolnaya-rabota-po-fizike-kinematika-9-klass/
