Задачи на движение
Продолжаем изучать элементарные задачи по математике. Данный урок посвящен задачам на движение.
Задача на нахождение расстояния/скорости/времени
Задача 1. Автомобиль двигается со скоростью 80 км/ч. Сколько километров он проедет за 3 часа?
Решение
Если за один час автомобиль проезжает 80 километров, то за 3 часа он проедет в три раза больше. Чтобы найти расстояние, нужно скорость автомобиля (80км/ч) умножить на время движения (3ч)
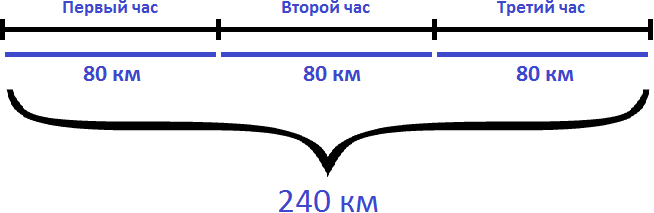
Ответ: за 3 часа автомобиль проедет 240 километров.
Задача 2. На автомобиле за 3 часа проехали 180 км с одной и той же скоростью. Чему равна скорость автомобиля?
Решение
Скорость — это расстояние, пройденное телом за единицу времени. Под единицей подразумевается 1 час, 1 минута или 1 секунда.
Если за 3 часа автомобиль проехал 180 километров с одной и той же скоростью, то разделив 180 км на 3 часа мы определим расстояние, которое проезжал автомобиль за один час. А это есть скорость движения. Чтобы определить скорость, нужно пройденное расстояние разделить на время движения:
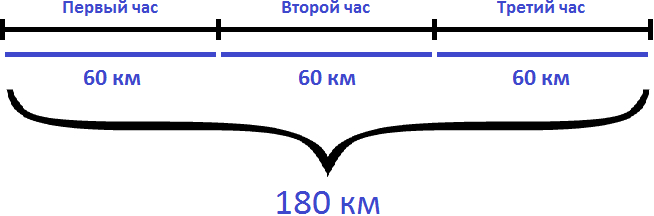
Ответ: скорость автомобиля составляет 60 км/ч
Задача 3. За 2 часа автомобиль проехал 96 км, а велосипедист за 6 часов проехал 72 км. Во сколько раз автомобиль двигался быстрее велосипедиста?
Решение
Определим скорость движения автомобиля. Для этого разделим пройденное им расстояние (96км) на время его движения (2ч)
Определим скорость движения велосипедиста. Для этого разделим пройденное им расстояние (72км) на время его движения (6ч)
Узнаем во сколько раз автомобиль двигался быстрее велосипедиста. Для этого найдем отношение 48 к 12
Ответ: автомобиль двигался быстрее велосипедиста в 4 раза.
Задача 4. Вертолет преодолел расстояние в 600 км со скоростью 120 км/ч. Сколько времени он был в полете?
Решение
Если за 1 час вертолет преодолевал 120 километров, то узнав сколько таких 120 километров в 600 километрах, мы определим сколько времени он был в полете. Чтобы найти время, нужно пройденное расстояние разделить на скорость движения
600 : 120 = 5 часов
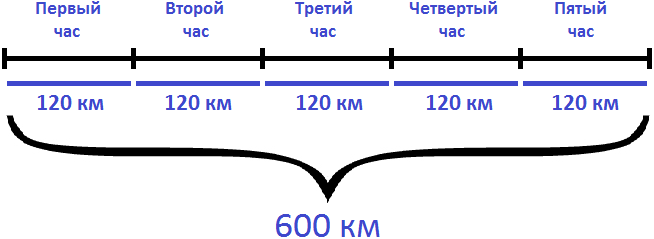
Ответ: вертолет был в пути 5 часов.
Задача 5. Вертолет летел 6 часов со скоростью 160 км/ч. Какое расстояние он преодолел за это время?
Решение
Если за 1 час вертолет преодолевал 160 км, то за 6 часов, он преодолел в шесть раз больше. Чтобы определить расстояние, нужно скорость движения умножить на время
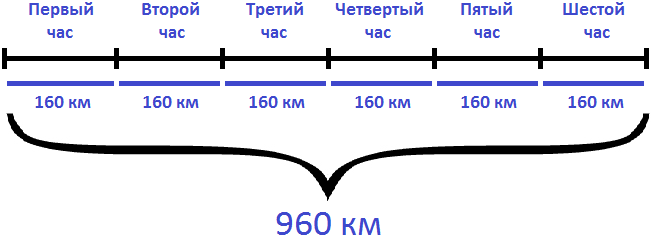
Ответ: за 6 часов вертолет преодолел 960 км.
Задача 6. Расстояние от Перми до Казани, равное 723 км, автомобиль проехал за 13 часов. Первые 9 часов он ехал со скоростью 55 км/ч. Определить скорость автомобиля в оставшееся время.
Решение
Определим сколько километров автомобиль проехал за первые 9 часов. Для этого умножим скорость с которой он ехал первые девять часов (55км/ч) на 9
Определим сколько осталось проехать. Для этого вычтем из общего расстояния (723км) расстояние, пройденное за первые 9 часов движения
723 − 495 = 228 км
Эти 228 километров автомобиль проехал за оставшиеся 4 часа. Чтобы определить скорость автомобиля в оставшееся время, нужно 228 километров разделить на 4 часа:
Ответ: скорость автомобиля в оставшееся время составляла 57 км/ч
Скорость сближения
Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причем скорость первого будет 100 м/м , а второго — 105 м/м , то скорость сближения будет составлять 100 + 105 , то есть 205 м/м . Это значит, что каждую минуту расстояние между пешеходами будет уменьшáться на 205 метров

Чтобы найти скорость сближения, нужно сложить скорости объектов.
Предположим, что пешеходы встретились через три минуты после начала движения. Зная, что они встретились через три минуты, мы можем узнать расстояние между двумя пунктами.
Каждую минуту пешеходы преодолевали расстояние равное двухсот пяти метрам. Через 3 минуты они встретились. Значит умножив скорость сближения на время движения, можно определить расстояние между двумя пунктами:
205 × 3 = 615 метров
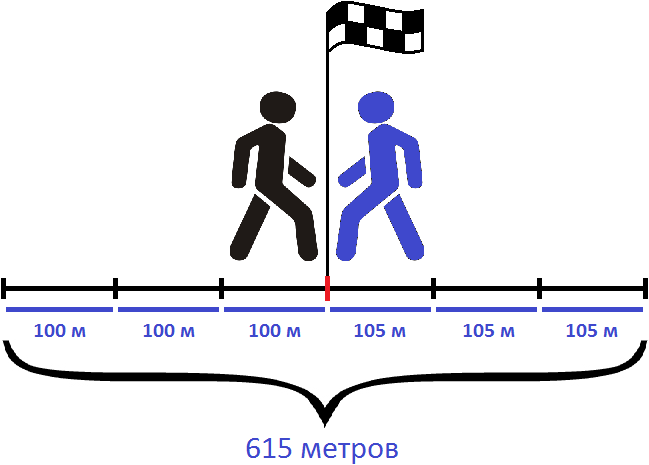
Можно и по другому определить расстояние между пунктами. Для этого следует найти расстояние, которое прошел каждый пешеход до встречи.
Так, первый пешеход шел со скоростью 100 метров в минуту. Встреча состоялась через три минуты, значит за 3 минуты он прошел 100 × 3 метров
100 × 3 = 300 метров
А второй пешеход шел со скоростью 105 метров в минуту. За три минуты он прошел 105 × 3 метров
105 × 3 = 315 метров
Теперь можно сложить полученные результаты и таким образом определить расстояние между двумя пунктами:
300 м + 315 м = 615 м
Задача 1. Из двух населенных пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 10 км/ч, а скорость второго — 12 км/ч. Через 2 часа они встретились. Определите расстояние между населенными пунктами
Решение
Найдем скорость сближения велосипедистов
10 км/ч + 12 км/ч = 22 км/ч
Определим расстояние между населенными пунктами. Для этого скорость сближения умножим на время движения
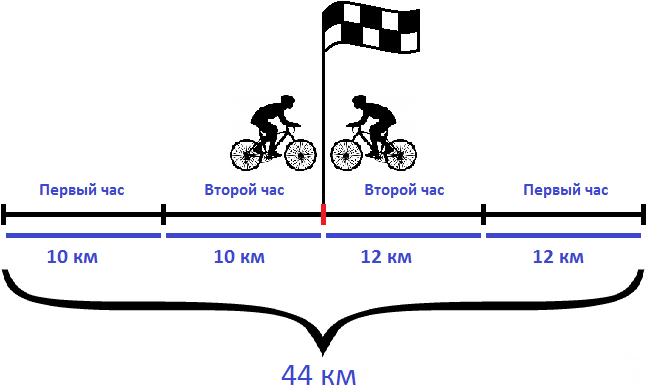
Решим эту задачу вторым способом. Для этого найдем расстояния, пройденные велосипедистами и сложим полученные результаты.
Найдем расстояние, пройденное первым велосипедистом:
Найдем расстояние, пройденное вторым велосипедистом:
Сложим полученные расстояния:
20 км + 24 км = 44 км
Ответ: расстояние между населенными пунктами составляет 44 км.
Задача 2. Из двух населенных пунктов, расстояние между которыми 60 км, навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 14 км/ч, а скорость второго — 16 км/ч. Через сколько часов они встретились?
Решение
Найдем скорость сближения велосипедистов:
14 км/ч + 16 км/ч = 30 км/ч
За один час расстояние между велосипедистами уменьшается на 30 километров. Чтобы определить через сколько часов они встретятся, нужно расстояние между населенными пунктами разделить на скорость сближения:
Значит велосипедисты встретились через два часа
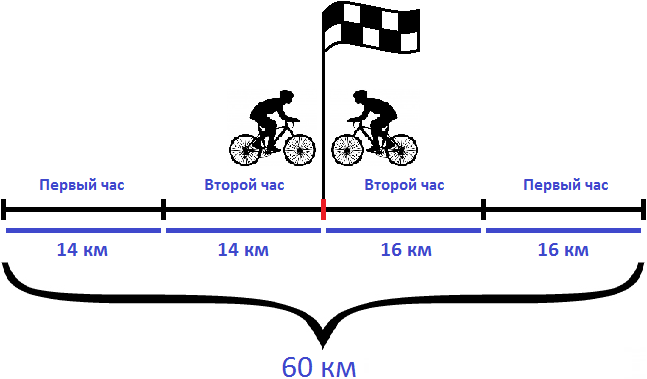
Ответ: велосипедисты встретились через 2 часа.
Задача 3. Из двух населенных пунктов, расстояние между которыми 56 км, навстречу друг другу выехали одновременно два велосипедиста. Через два часа они встретились. Первый велосипедист ехал со скоростью 12 км/ч. Определить скорость второго велосипедиста.
Решение
Определим расстояние пройденное первым велосипедистом. Как и второй велосипедист в пути он провел 2 часа. Умножив скорость первого велосипедиста на 2 часа, мы сможем узнать сколько километров он прошел до встречи
За два часа первый велосипедист прошел 24 км. За один час он прошел 24:2, то есть 12 км. Изобразим это графически
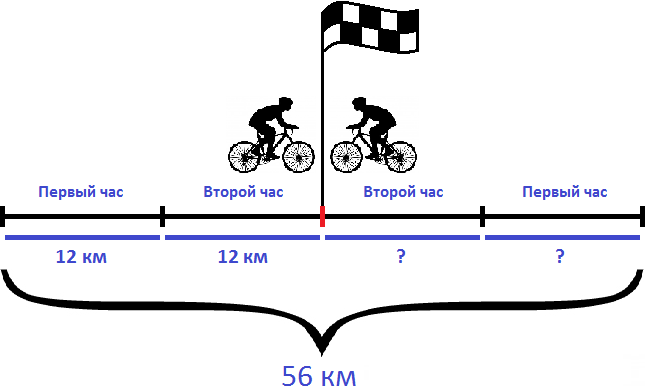
Вычтем из общего расстояния (56 км) расстояние, пройденное первым велосипедистом (24 км). Так мы определим сколько километров прошел второй велосипедист:
56 км − 24 км = 32 км
Второй велосипедист, как и первый провел в пути 2 часа. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
Значит скорость второго велосипедиста составляет 16 км/ч.
Ответ: скорость второго велосипедиста составляет 16 км/ч.
Скорость удаления
Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причем скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4+6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиться на 10 километров.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Так, за первый час расстояние между пешеходами будет составлять 10 километров. На следующем рисунке можно увидеть, как это происходит
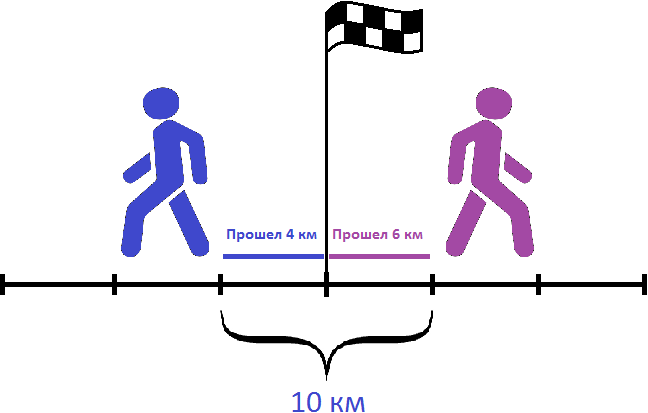
Видно, что первый пешеход прошел свои 4 километра за первый час. Второй пешеход также прошел свои 6 километров за первый час. Итого за первый час расстояние между ними стало 4+6, то есть 10 километров.
Через два часа расстояние между пешеходами будет составлять 10×2, то есть 20 километров. На следующем рисунке можно увидеть, как это происходит:
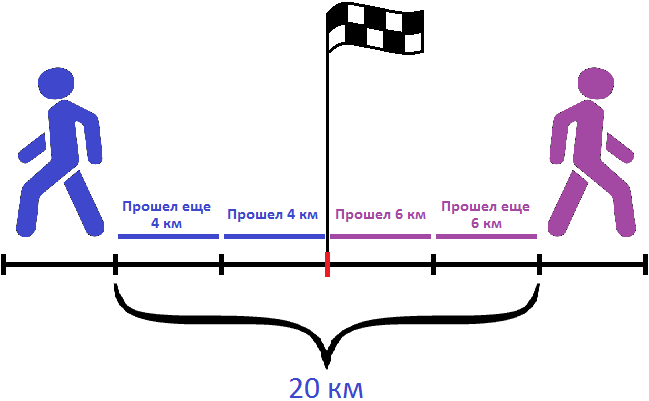
Задача 1. От одной станции отправились одновременно в противоположных направлениях товарный поезд и пассажирский экспресс. Скорость товарного поезда составляла 40 км/ч, скорость экспресса 180 км/ч. Какое расстояние будет между этими поездами через 2 часа?
Решение
Определим скорость удаления поездов. Для этого сложим их скорости:
40 + 180 = 220 км/ч
Получили скорость удаления поездов равную 220 км/ч. Данная скорость показывает, что за час расстояние между поездами будет увеличиваться на 220 километров. Чтобы узнать какое расстояние будет между поездами через два часа, нужно 220 умножить на 2
Ответ: через 2 часа расстояние будет между поездами будет 440 километров.
Задача 2. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 16 км/ч, а скорость мотоциклиста — 40 км/ч. Какое расстояние будет между велосипедистом и мотоциклистом через 2 часа?
Решение
Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:
16 км/ч + 40 км/ч = 56 км/ч
Определим расстояние, которое будет между велосипедистом и мотоциклистом через 2 часа. Для этого скорость удаления (56км/ч) умножим на 2 часа
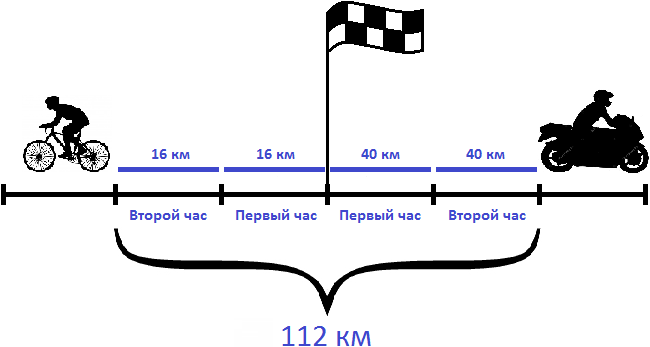
Ответ: через 2 часа расстояние между велосипедистом и мотоциклистом будет 112 км.
Задача 3. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 10 км/ч, а скорость мотоциклиста — 30 км/ч. Через сколько часов расстояние между ними будет 80 км?
Решение
Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:
10 км/ч + 30 км/ч = 40 км/ч
За один час расстояние между велосипедистом и мотоциклистом увеличивается на 40 километров. Чтобы узнать через сколько часов расстояние между ними будет 80 км, нужно определить сколько раз 80 км содержит по 40 км
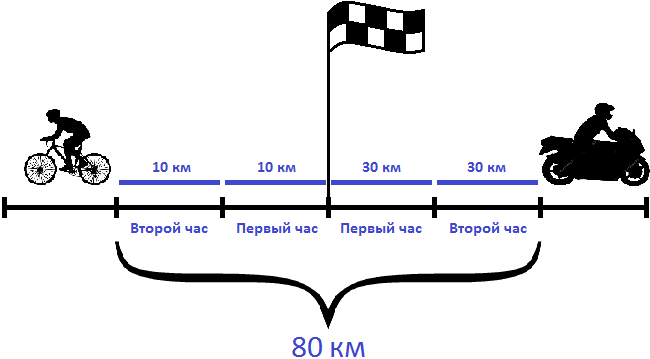
Ответ: через 2 часа после начала движения, между велосипедистом и мотоциклистом будет 80 километров.
Задача 4. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Через 2 часа расстояние между ними было 90 км. Скорость велосипедиста составляла 15 км/ч. Определить скорость мотоциклиста
Решение
Определим расстояние, пройденное велосипедистом за 2 часа. Для этого умножим его скорость (15 км/ч) на 2 часа
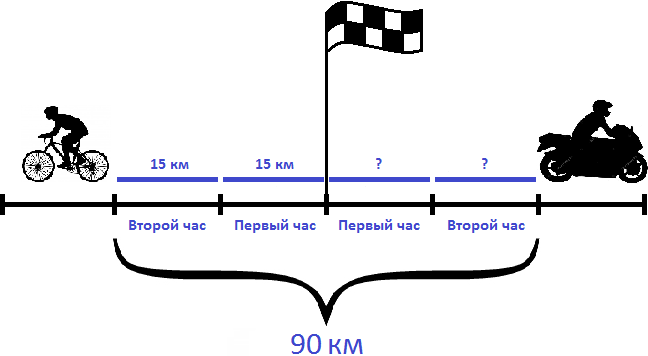
На рисунке видно, что велосипедист прошел по 15 километров в каждом часе. Итого за два часа он прошел 30 километров.
Вычтем из общего расстояния (90 км) расстояние, пройденное велосипедистом (30 км). Так мы определим сколько километров прошел мотоциклист:
90 км − 30 км = 60 км
Мотоциклист за два часа прошел 60 километров. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
Значит скорость мотоциклиста составляла 30 км/ч.
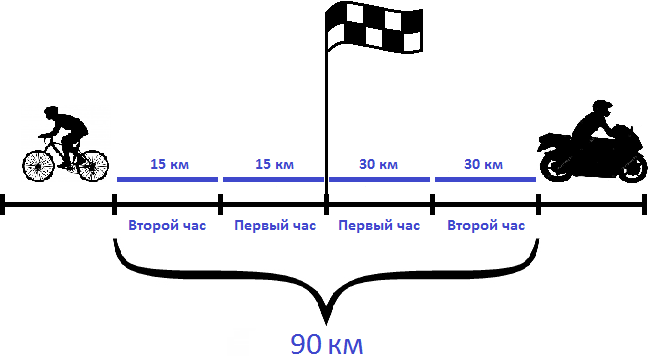
Ответ: скорость мотоциклиста составляла 30 км/ч.
Задача на движение объектов в одном направлении
В предыдущей теме мы рассматривали задачи в которых объекты (люди, машины, лодки) двигались либо навстречу другу другу либо в противоположных направлениях. При этом мы находили различные расстояния, которые изменялись между объектами в течении определенного времени. Эти расстояния были либо скоростями сближения либо скоростями удаления.
В первом случае мы находили скорость сближения — в ситуации, когда два объекта двигались навстречу друг другу. За единицу времени расстояние между объектами уменьшалось на определенное расстояние

Во втором случае мы находили скорость удаления — в ситуации, когда два объекта двигались в противоположных направлениях. За единицу времени расстояние между объектами увеличивалось на определенное расстояние

Но объекты также могут двигаться в одном направлении, причем с различной скоростью. Например, из одного пункта одновременно могут выехать велосипедист и мотоциклист, причем скорость велосипедиста может составлять 20 километров в час, а скорость мотоциклиста — 40 километров в час
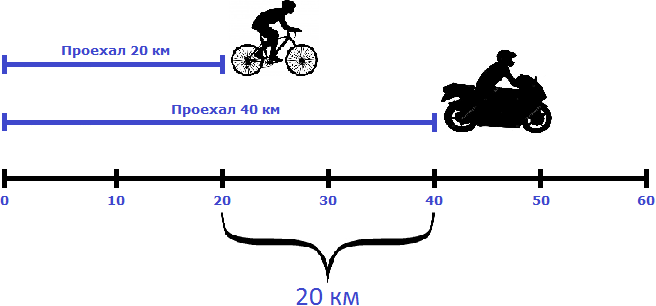
На рисунке видно, что мотоциклист впереди велосипедиста на двадцать километров. Связано это с тем, что в час он преодолевает на 20 километров больше, чем велосипедист. Поэтому каждый час расстояние между велосипедистом и мотоциклистом будет увеличиваться на двадцать километров.
В данном случае 20 км/ч являются скоростью удаления мотоциклиста от велосипедиста.
Через два часа расстояние, пройденное велосипедистом будет составлять 40 км. Мотоциклист же проедет 80 км, отдалившись от велосипедиста еще на двадцать километров — итого расстояние между ними составит 40 километров
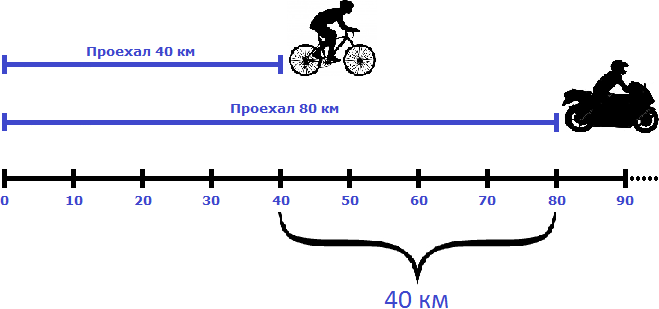
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
В приведенном выше примере, скорость удаления составляет 20 км/ч. Её можно найти путем вычитания скорости велосипедиста из скорости мотоциклиста. Скорость велосипедиста составляла 20 км/ч, а скорость мотоциклиста — 40 км/ч. Скорость мотоциклиста больше, поэтому из 40 вычитаем 20
40 км/ч − 20 км/ч = 20 км/ч
Задача 1. Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 120 км/ч, а скорость автобуса 80 км/ч. Какое расстояние будет между ними через 1 час? 2 часа?
Решение
Найдем скорость удаления. Для этого из большей скорости вычтем меньшую
120 км/ч − 80 км/ч = 40 км/ч
Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 2 часа в два раза больше:
Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через два часа — 80 км.
Рассмотрим ситуацию в которой объекты начали свое движение из разных пунктов, но в одном направлении.
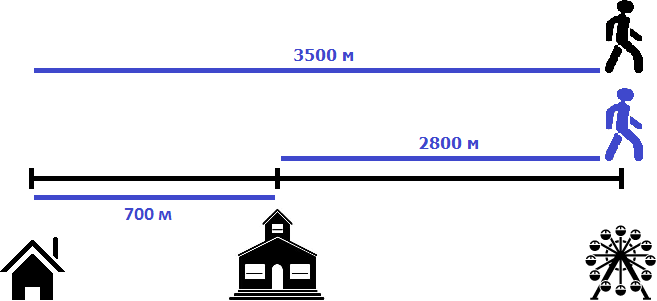
Пусть имеется дом, школа и аттракцион. От дома до школы 700 метров
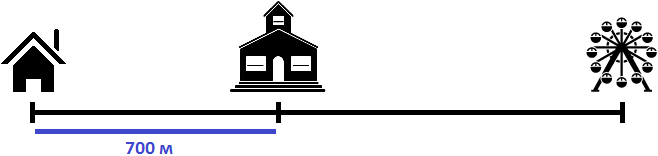
Два пешехода отправились в аттракцион в одно и то же время. Причем первый пешеход отправился в аттракцион от дома со скоростью 100 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 80 метров в минуту. Какое расстояние будет между пешеходами через 2 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Ответим на первый вопрос задачи — какое расстояние будет между пешеходами через 2 минуты?
Определим расстояние, пройденное первым пешеходом за 2 минуты. Он двигался со скоростью 100 метров в минуту. За две минуты он пройдет в два раза больше, то есть 200 метров
100 × 2 = 200 метров
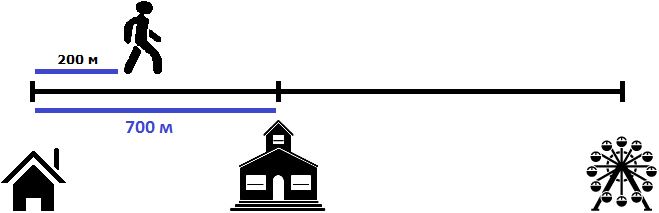
Определим расстояние, пройденное вторым пешеходом за 2 минуты. Он двигался со скоростью 80 метров в минуту. За две минуты он пройдет в два раза больше, то есть 160 метров
80 × 2 = 160 метров
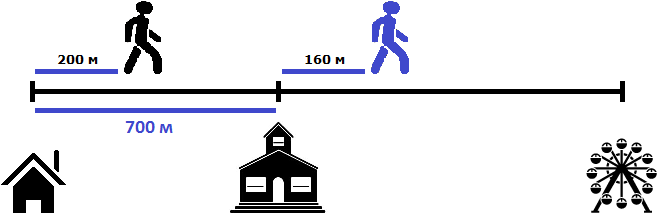
Теперь нужно найти расстояние между пешеходами
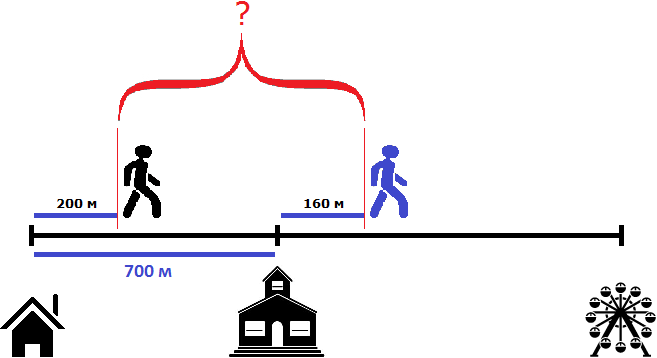
Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (700м) прибавить расстояние, пройденное вторым пешеходом (160м) и из полученного результата вычесть расстояние, пройденное первым пешеходом (200м)
700 м + 160 м = 860 м
860 м − 200 м = 660 м
Либо из расстояния от дома до школы (700м) вычесть расстояние, пройденное первым пешеходом (200м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (160м)
700 м − 200 м = 500 м
500 м + 160 м = 660 м
Таким образом, через две минуты расстояние между пешеходами будет составлять 660 метров
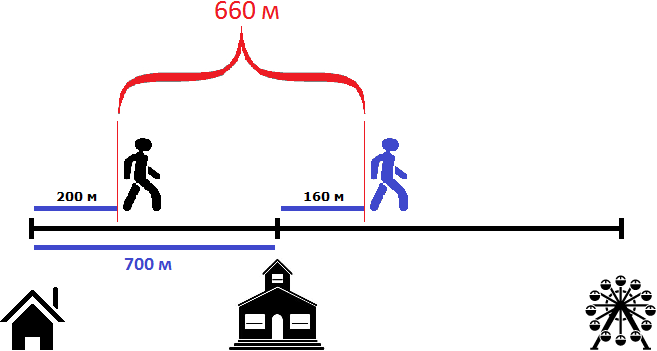
Попробуем ответить на следующий вопрос задачи: через сколько минут после начала движения первый пешеход догонит второго?
Давайте посмотрим какой была ситуация в самом начале пути — когда пешеходы еще не начали своё движение
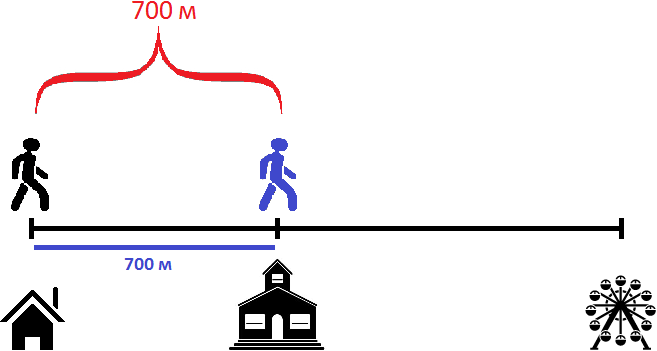
Как видно на рисунке, расстояние между пешеходами в начале пути составляло 700 метров. Но уже через минуту после начала движения расстояние между ними будет составлять 680 метров, поскольку первый пешеход двигается на 20 метров быстрее второго:
100 м × 1 = 100 м
700 м + 80 м − 100 м = 780 м − 100 м = 680 м
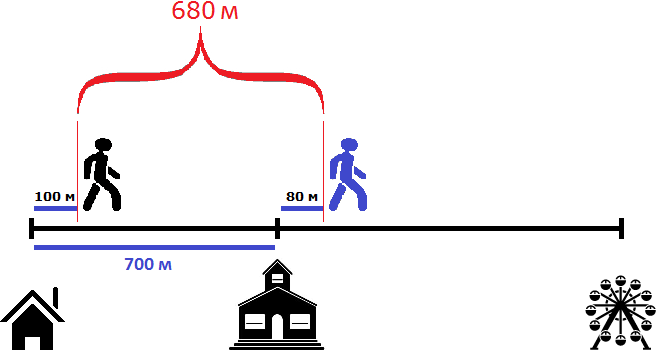
Через две минуты после начала движения, расстояние уменьшится еще на 20 метров и будет составлять 660 метров. Это был наш ответ на первый вопрос задачи:
100 м × 2 = 200 м
700 м + 160 м − 200м = 860 м − 200 м = 660 м

Через три минуты расстояние уменьшится еще на 20 метров и будет уже составлять 640 метров:
100 м × 3 = 300 м
700 м + 240 м − 300м = 940 м − 300 м = 640 м
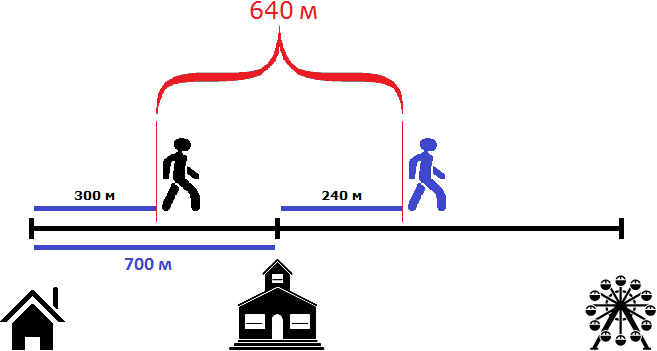
Мы видим, что с каждой минутой первый пешеход будет приближáться ко второму на 20 метров, и в конце концов догонит его. Можно сказать, что скорость равная двадцати метрам в минуту является скоростью сближения пешеходов. Правила нахождения скорости сближения и удаления при движении в одном направлении идентичны.
Чтобы найти скорость сближения при движении в одном направлении, нужно из большей скорости вычесть меньшую.
А раз изначальные 700 метров с каждой минутой уменьшаются на одинаковые 20 метров, то мы можем узнать сколько раз 700 метров содержат по 20 метров, тем самым определяя через сколько минут первый пешеход догонит второго
Значит через 35 минут после начала движения первый пешеход догонит второго. Для интереса узнаем сколько метров прошел к этому времени каждый пешеход. Первый двигался со скоростью 100 метров в минуту. За 35 минут он прошел в 35 раз больше
100 × 35 = 3500 м
Второй шел со скоростью 80 метров в минуту. За 35 минут он прошел в 35 раз больше
Первый прошел 3500 метров, а второй 2800 метров. Первый прошел на 700 метров больше, поскольку он шел от дома. Если вычесть эти 700 метров из 3500, то мы получим 2800 м
Рассмотрим ситуацию в которой объекты движутся в одном направлении, но один из объектов начал своё движение раньше другого.
Пусть имеется дом и школа. Первый пешеход отправился в школу со скоростью 80 метров в минуту. Через 5 минут вслед за ним в школу отправился второй пешеход со скоростью 100 метров в минуту. Через сколько минут второй пешеход догонит первого?
Второй пешеход начал свое движение через 5 минут. К этому времени первый пешеход уже отдалился от него на какое-то расстояние. Найдём это расстояние. Для этого умножим его скорость (80 м/м) на 5 минут
80 × 5 = 400 метров
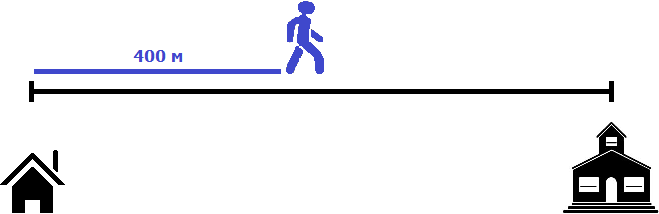
Первый пешеход отдалился от второго на 400 метров. Поэтому в момент, когда второй пешеход начнет свое движение, между ними будут эти самые 400 метров.
Но второй пешеход двигается со скоростью 100 метров в минуту. То есть двигается на 20 метров быстрее первого пешехода, а значит с каждой минутой расстояние между ними будет уменьшáться на 20 метров. Наша задача узнать через сколько минут это произойдет.
Например, уже через минуту расстояние между пешеходами будет составлять 380 метров. Первый пешеход к своим 400 метрам пройдет еще 80 метров, а второй пройдет 100 метров
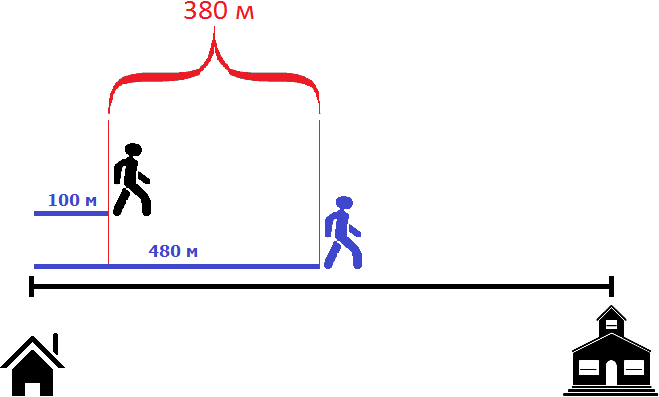
Принцип здесь такой-же, как и в предыдущей задаче. Расстояние между пешеходами в момент движения второго пешехода необходимо разделить на скорость сближения пешеходов. Скорость сближения в данном случае равна двадцати метрам. Поэтому, чтобы определить через сколько минут второй пешеход догонит первого, нужно 400 метров разделить на 20
Значит через 20 минут второй пешеход догонит первого.
Задача 2. Из двух сел, расстояние между которыми 40 км, одновременно в одном направлении выехали автобус и велосипедист. Скорость велосипедиста 15 км/ч, а скорость автобуса 35 км/ч. Через сколько часов автобус догонит велосипедиста?
Решение
Найдем скорость сближения
35 км/ч − 15 км/ч = 20 км/ч
Определим через часов автобус догонит велосипедиста
Ответ: автобус догонит велосипедиста через 2 часа.
Задача на движение по реке
Суда двигаются по реке с различной скоростью. При этом они могут двигаться, как по течению реки, так и против течения. В зависимости от того, как они двигаются (по или против течения), скорость будет меняться.
Предположим, что скорость реки составляет 3 км/ч. Если спустить лодку на реку, то река унесет лодку со скоростью 3 км/ч.
Если спустить лодку на стоячую воду, в которой отсутствует течение, то и лодка будет стоять. Скорость движения лодки в этом случае будет равна нулю.
Если лодка плывет по стоячей воде, в которой отсутствует течение, то говорят, что лодка плывет с собственной скоростью.
Например, если моторная лодка плывет по стоячей воде со скоростью 40 км/ч, то говорят что собственная скорость моторной лодки составляет 40 км/ч.
Как определить скорость судна?
Если судно плывет по течению реки, то к собственной скорости судна нужно прибавить скорость течения реки.
Например, если моторная лодка плывет со скоростью 30 км/ч по течению реки, и скорость течения реки составляет 2 км/ч, то к собственной скорости моторной лодки (30 км/ч) необходимо прибавить скорость течения реки (2 км/ч)
30 км/ч + 2 км/ч = 32 км/ч
Течение реки можно сказать помогает моторной лодке дополнительной скоростью равной двум километрам в час.
Если судно плывет против течения реки, то из собственной скорости судна нужно вычесть скорость течения реки.
Например, если моторная лодка плывет со скоростью 30 км/ч против течения реки, и скорость течения реки составляет 2 км/ч, то из собственной скорости моторной лодки (30 км/ч) необходимо вычесть скорость течения реки (2 км/ч)
30 км/ч − 2 км/ч = 28 км/ч
Течение реки в этом случае препятствует моторной лодке свободно двигаться вперед, снижая её скорость на два километра в час.
Задача 1. Скорость катера 40 км/ч, а скорость течения реки 3 км/ч. С какой скоростью катер будет двигаться по течению реки? Против течения реки?
Ответ:
Если катер будет двигаться по течения реки, то скорость его движения составит 40 + 3, то есть 43 км/ч.
Если катер будет двигаться против течения реки, то скорость его движения составит 40 − 3, то есть 37 км/ч.
Задача 2. Скорость теплохода в стоячей воде — 23 км/ч. Скорость течения реки — 3 км/ч. Какой путь пройдет теплоход за 3 часа по течению реки? Против течения?
Решение
Собственная скорость теплохода составляет 23 км/ч. Если теплоход будет двигаться по течению реки, то скорость его движения составит 23 + 3, то есть 26 км/ч. За три часа он пройдет в три раза больше
Если теплоход будет двигаться против течения реки, то скорость его движения составит 23 − 3, то есть 20 км/ч. За три часа он пройдет в три раза больше
Задача 3. Расстояние от пункта А до пункта B лодка преодолела за 3 часа 20 минут, а расстояние от пункта B до А — за 2 часа 50 минут. В каком направлении течет река: от А к В или от В к А, если известно, что скорость яхты не менялась?
Решение
Скорость яхты не менялась. Узнаем на какой путь она затратила больше времени: на путь от А до В или на путь от В до А. Тот путь, который затратил больше времени будет тем путем, течение реки которого шло против яхты
3 часа 20 минут больше, чем 2 часа 50 минут. Это значит, что течение реки снизило скорость яхты и это отразилось на времени пути. 3 часа 20 минут это время, затраченное на путь от от А до В. Значит река течет от пункта B к пункту А
Задача 4. За какое время при движении против течения реки
теплоход пройдет 204 км, если его собственная скорость
15 км/ч, а скорость течения в 5 раз меньше собственной
скорости теплохода?
Решение
Требуется найти время за которое теплоход пройдет 204 километра против течения реки. Собственная скорость теплохода составляет 15 км/ч. Двигается он против течения реки, поэтому нужно определить его скорость при таком движении.
Чтобы определить скорость против течения реки, нужно из собственной скорости теплохода (15 км/ч) вычесть скорость движения реки. В условии сказано, что скорость течения реки в 5 раз меньше собственной скорости теплохода, поэтому сначала определим скорость течения реки. Для этого уменьшим 15 км/ч в пять раз
Скорость течения реки составляет 3 км/ч. Вычтем эту скорость из скорости движения теплохода
15 км/ч − 3 км/ч = 12 км/ч
Теперь определим время за которое теплоход пройдет 204 км при скорости 12 км/ч. В час теплоход проходит 12 километров. Чтобы узнать за сколько часов он пройдет 204 километра, нужно определить сколько раз 204 километра содержит по 12 километров
Ответ: теплоход пройдет 204 километра за 17 часов
Задача 5. Двигаясь по течению реки, за 6 часов лодка
прошла 102 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.
Решение
Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (102км) разделим на время движения (6ч)
Определим собственную скорость лодки. Для этого из скорости по которой она двигалась по реке (17 км/ч) вычтем скорость течения реки (4 км/ч)
Задача 6. Двигаясь против течения реки, за 5 часов лодка
прошла 110 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.
Решение
Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (110км) разделим на время движения (5ч)
Определим собственную скорость лодки. В условии сказано, что она двигалась против течения реки. Скорость течения реки составляла 4 км/ч. Это значит, что собственная скорость лодки была уменьшена на 4. Наша задача прибавить эти 4 км/ч и узнать собственную скорость лодки
Ответ: собственная скорость лодки составляет 26 км/ч
Задача 7. За какое время при движении против течения реки лодка
пройдет 56 км, если скорость течения – 2 км/ч, а её
собственная скорость на 8 км/ч больше скорости течения?
Решение
Найдем собственную скорость лодки. В условии сказано, что она на 8 км/ч больше скорости течения. Поэтому для определения собственной скорости лодки, к скорости течения (2 км/ч) прибавим еще 8 км/ч
2 км/ч + 8 км/ч = 10 км/ч
Лодка движется против течения реки, поэтому из собственной скорости лодки (10 км/ч) вычтем скорость движения реки (2 км/ч)
10 км/ч − 2 км/ч = 8 км/ч
Узнаем за какое время лодка пройдет 56 км. Для этого расстояние (56км) разделим на скорость движения лодки:
Ответ: при движении против течения реки лодка пройдет 56 км за 7 часов
Задачи для самостоятельного решения
Решение
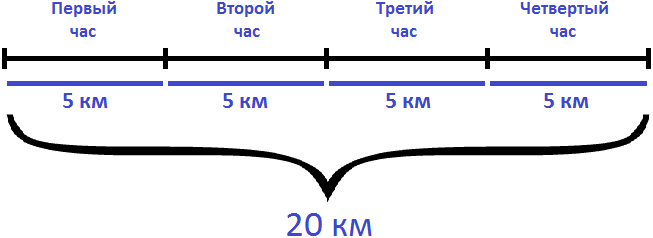
За один час пешеход проходит 5 километров. Чтобы определить за какое время он пройдет 20 км, нужно узнать сколько раз 20 километров содержат по 5 км. Либо воспользоваться правилом нахождения времени: разделить пройденное расстояние на скорость движения
Решение
Определим расстояние от пункта А до пункта В. Для этого умножим скорость с которой ехал велосипедист из пункта А в пункт В (16км/ч) на время движения (5ч)
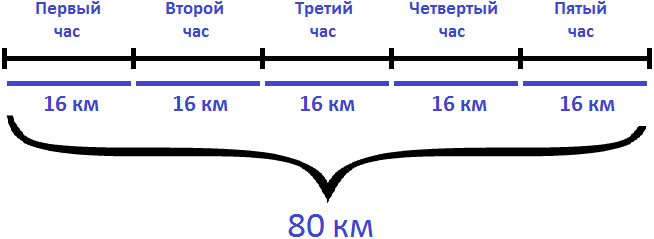
Определим сколько времени велосипедист затратил на обратный путь. Для этого расстояние (80км) разделим на скорость движения (10км/ч)
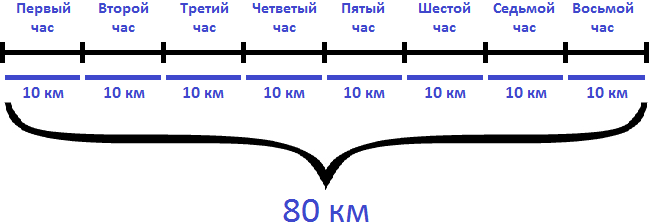
Решение
Определим путь, пройденный велосипедистом за 6 часов. Для этого из 83 км вычтем путь, который он прошел после шести часов движения (11км)
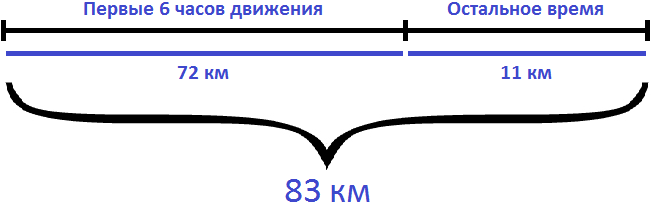
Определим с какой скоростью ехал велосипедист первые 6 часов. Для этого разделим 72 км на 6 часов
Поскольку в условии задаче сказано, что остальные 11 км велосипедист проехал с той же скоростью, что и в первые 6 часов движения, то скорость равная 12 км/ч является ответом к задаче.
Ответ: велосипедист ехал со скоростью 12 км/ч.
Решение
Найдем скорость течения реки. В условии сказано, что плот может проплыть 72 километра за 36 часов. Плот не может двигаться против течения реки. Значит скорость плота с которой он преодолевает эти 72 километра и является скоростью течения реки. Чтобы найти эту скорость, нужно 72 километра разделить на 36 часов
Найдем собственную скорость теплохода. Сначала найдем скорость его движения против течения реки. Для этого разделим 72 километра на 4 часа
Если против течения реки скорость теплохода составляет 18 км/ч, то собственная его скорость равна 18+2, то есть 20 км/ч. А по течению реки его скорость будет составлять 20+2, то есть 22 км/ч
Разделив 110 километров на скорость движения теплохода по течению реки (22 км/ч), можно узнать за сколько часов теплоход проплывет эти 110 километров
Ответ: по течению реки теплоход проплывет 110 километров за 5 часов.
Решение
Найдем скорость удаления велосипедистов
Узнаем какое расстояние будет между ними через 4 часа
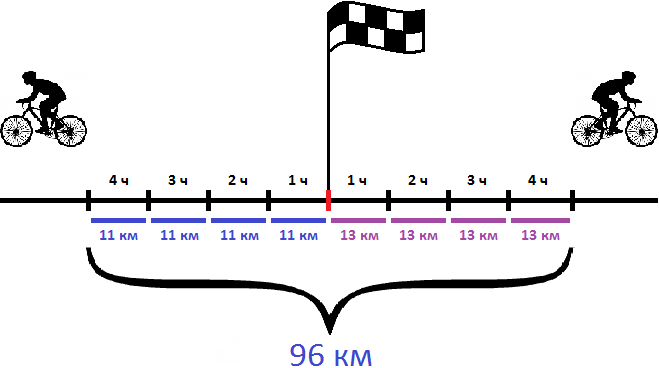
Ответ: через 4 часа расстояние между велосипедистами будет 96 км.
Решение
Определим расстояние, пройденное первым теплоходом. Для этого умножим его скорость (21 км/ч) на время движения до встречи (6ч)
Определим расстояние, пройденное вторым теплоходом. Для этого умножим его скорость (24 км/ч) на время движения до встречи (6ч)
Определим расстояние между пристанями. Для этого сложим расстояния, пройденные первым и вторым теплоходами
126 км + 144 км = 270 км
Ответ: первый теплоход прошел 126 км, второй — 144 км. Расстояние между пристанями составляет 270 км.
Решение
Определим сколько километров до встречи прошел поезд, вышедший из Москвы. Для этого умножим его скорость (51 км/ч) на 16 часов
Узнаем сколько километров до встречи прошел поезд, вышедший из Уфы. Для этого из расстояния между Москвой и Уфой (1520км) вычтем расстояние, пройденное поездом, вышедшим из Москвы
1520 − 816 = 704 км
Определим скорость с которой шел поезд, вышедший из Уфы. Для этого расстояние, пройденное им до встречи, нужно разделить на 16 часов
704 : 16 = 44 км/ч
Определим расстояние, которое будет между поездами через 5 часов после их встречи. Для этого найдем скорость удаления поездов и умножим эту скорость на 5
51 км/ч + 44 км/ч = 95 км/ч
Ответ: поезд, вышедший из Уфы, шел со скоростью 44 км/ч. Через 5 часов после их встречи поездов расстояние между ними будет составлять 475 км.
Решение
Найдем скорость второго автобуса. Она на 6 км/ч больше скорости первого автобуса
48 км/ч + 6 км/ч = 54 км/ч
Найдем скорость удаления автобусов. Для этого сложим их скорости:
48 км/ч + 54 км/ч = 102 км/ч
За час расстояние между автобусами увеличивается на 102 километра. Чтобы узнать через сколько часов расстояние между ними будет 510 км, нужно узнать сколько раз 510 км содержит по 102 км/ч
Ответ: 510 км между автобусами будет через 5 часов.
Задача 9. Расстояние от Ростова-на-Дону до Москвы 1230 км. Из Москвы и Ростова навстречу друг другу вышли два поезда. Поезд из Москвы идет со скоростью 63 км/ч, а скорость ростовского поезда составляет скорости московского поезда. На каком расстоянии от Ростова встретятся поезда?
Решение
Найдем скорость ростовского поезда. Она составляет />скорости московского поезда. Поэтому чтобы определить скорость ростовского поезда, нужно найти />от 63 км
63 : 21 × 20 = 3 × 20 = 60 км/ч
Найдем скорость сближения поездов
63 км/ч + 60 км/ч = 123 км/ч
Определим через сколько часов поезда встретятся
1230 : 123 = 10 ч
Узнаем на каком расстоянии от Ростова встретятся поезда. Для этого достаточно найти расстояние, пройденное ростовским поездом до встречи
Ответ: поезда встретятся на расстоянии 600 км от Ростова.
Решение
Найдем скорость второй лодки. Она составляет 75% скорости первой лодки. Поэтому чтобы найти скорость второй лодки, нужно 75% от 16 км
16 × 0,75 = 12 км/ч
Найдем скорость сближения лодок
16 км/ч + 12 км/ч = 28 км/ч
С каждым часом расстояние между лодками будет уменьшáться на 28 км. Через 2 часа оно уменьшится на 28×2, то есть на 56 км. Чтобы узнать какое будет расстояние между лодками в этот момент, нужно из 75 км вычесть 56 км
75 км − 56 км = 19 км
Ответ: через 2 часа между лодками будет 19 км.
Решение
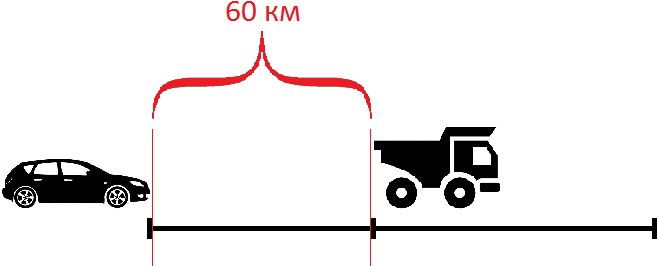
Найдем скорость сближения
62 км/ч − 47 км/ч = 15 км/ч
Если первоначально расстояние между машинами было 60 километров, то с каждым часом это расстояние будет уменьшáться на 15 км, и в конце концов легковая машина догонит грузовую. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 60 км содержит по 15 км
Узнаем на каком расстоянии от начала движения легковая машина догнала грузовую. Для этого умножим скорость легковой машины (62 км/ч) на время её движения до встречи (4ч)
Ответ: легковая машина догонит грузовую через 4 часа. В момент встречи легковая машина будет на расстоянии 248 км от начала движения.
Решение
Найдем скорость второго мотоциклиста. Она составляет 80% скорости первого мотоциклиста. Поэтому чтобы найти скорость второго мотоциклиста, нужно найти 80% от 35 км/ч
35 × 0,80 = 28 км/ч
Первый мотоциклист двигается на 35-28 км/ч быстрее
35 км/ч − 28 км/ч = 7 км/ч
За один час первый мотоциклиста преодолевает на 7 километров больше. С каждым часом она будет приближáться ко второму мотоциклисту на эти 7 километров.
Через 5 часов первый мотоциклист пройдет 35×5, то есть 175 км, а второй мотоциклист пройдет 28×5, то есть 140 км. Определим расстояние, которое между ними. Для этого из 175 км вычтем 140 км
175 − 140 = 35 км
Ответ: через 5 часов расстояние между мотоциклистами будет 35 км.
Решение
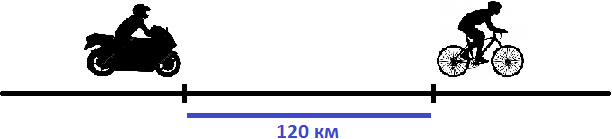
Найдем скорость сближения:
43 км/ч − 13 км/ч = 30 км/ч
Если первоначально расстояние между мотоциклистом и велосипедистом было 120 километров, то с каждым часом это расстояние будет уменьшáться на 30 км, и в конце концов мотоциклист догонит велосипедиста. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 120 км содержит по 30 км
Значит через 4 часа мотоциклист догонит велосипедиста
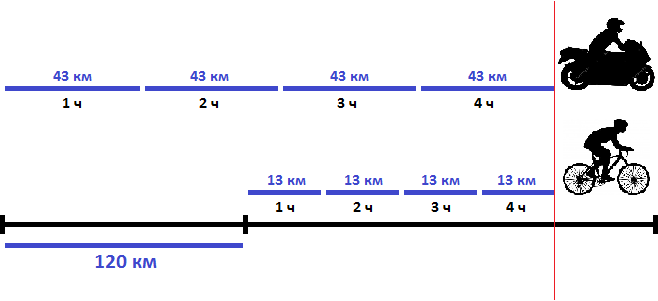
На рисунке представлено движение мотоциклиста и велосипедиста. Видно, что через 4 часа после начала движения они сровнялись.
Ответ: мотоциклист догонит велосипедиста через 4 часа.
Решение
Определим скорость велосипедиста, ехавшего впереди. Для этого найдем 75% от скорости велосипедиста, ехавшего сзади:
12 × 0,75 = 9 км/ч — скорость ехавшего впереди
Узнаем сколько километров проехал каждый велосипедист до того, как второй догнал первого:
12 × 6 = 72 км — проехал ехавший сзади
9 × 6 = 54 км — проехал ехавший впереди
Узнаем какое расстояние было между велосипедистами первоначально. Для этого из расстояния, пройденного вторым велосипедистом (который догонял) вычтем расстояние, пройденное первым велосипедистом (которого догнали)
72 км − 54 км = 18 км
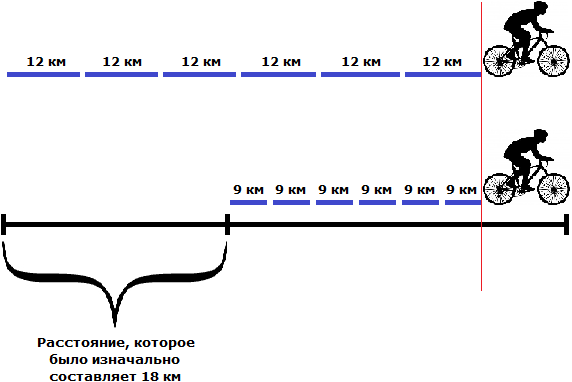
Ответ: между велосипедистами первоначально было 18 км.
Решение
Найдем скорость удаления автомобиля от автобуса
53 км/ч − 41 км/ч = 12 км/ч
С каждым часом автомобиль будет удаляться от автобуса на 12 километров. На рисунке показано положение машин после первого часа движения
Видно, что автомобиль впереди автобуса на 12 км.
Чтобы узнать через сколько часов автомобиль будет впереди автобуса на 48 километров, нужно определить сколько раз 48 км содержит по 12 км
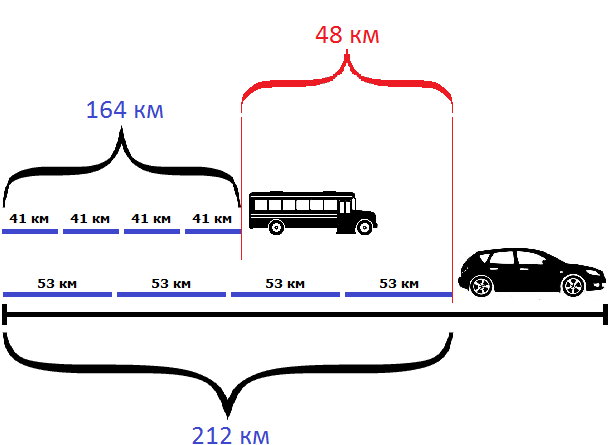
Ответ: через 4 часа после выезда автомобиль будет впереди автобуса на 48 километров.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
19 thoughts on “Задачи на движение”
Здравствуйте. Как решить такую задачу? Она вроде, и на движение, и на уравнение, но никак не мог понять как ее составить и решить.
Моторная лодка прошла против течения реки 297 км и вернулась в пункт отправления, затратив на обратный путь на 3 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 2 км/ч.
Задача на составление уравнения, содержащего рациональные выражения. В данном уроке такие задачи не рассмотрены. Обычно их решают в процессе изучения рациональных выражений.
x — скорость лодки в неподвижной воде
x — 2 — скорость лодки против течения
x + 2 — скорость лодки по течению
297/x-2 — время движения против течения
297/x+2 — время движения по течению
55 километров на велосипеде за 1 час, 139 326 в год и другие рекорды.

Не мудрено, что с появлением и распространением велосипедов стали появляться и самые разные рекорды с ними связанные. Разделить их можно на технические и спортивные. Именно о последних мы сегодня вам и расскажем. Всё же, пределы человеческой выносливости нам кажутся интереснее технических данных.
Кстати, если вам известны и другие велосипедные достижения, о которых мы не упомянули, то милости просим в комментарии нашей группы в Facebook.
1. Часовой рекорд

Часовая гонка считается едва ли не самой главной и престижной в мире велогонок. Заключается она в преодолении максимальной дистанции за 60 минут времени в условиях велодрома.
Первый рекорд принято датировать 1876 годом, когда гонщику удалось преодолеть 26,508 км. Рекорд 2019 года составляет 55,089 км и поставлен он Виктором Кампенэртсом после ослабления ограничений по велосипедам со стороны UCI.
Женский рекорд установлен Витторией Бусси и составляет 48,007 км.
Кстати, оба рекорда были поставлены на высоте 2 000 метров над уровнем моря в Агуаскальентес, Мексика.
2. Максимальное расстояние за 1 минуту на тренажере.

Кому бы такое могло вообще в голову прийти? Тем не менее, и такой рекорд есть. Он был поставлен Мигелем Анхелем Кастро в 2009 году, велосипедисту удалось проехать 2 040 метров за 60 секунд. Много это или мало? Что ж, достаточно сказать, что он развил скорость 122,31 км/ч. Получается, что много. Так ведь? Не совсем. В 2015 году Кастро побил собственный рекорд и проехал уже 3 060 метров, где средняя скорость составляла 183,6 км/ч.
3. Самый быстрый заезд от Края Земли до Джона О’Гроута.
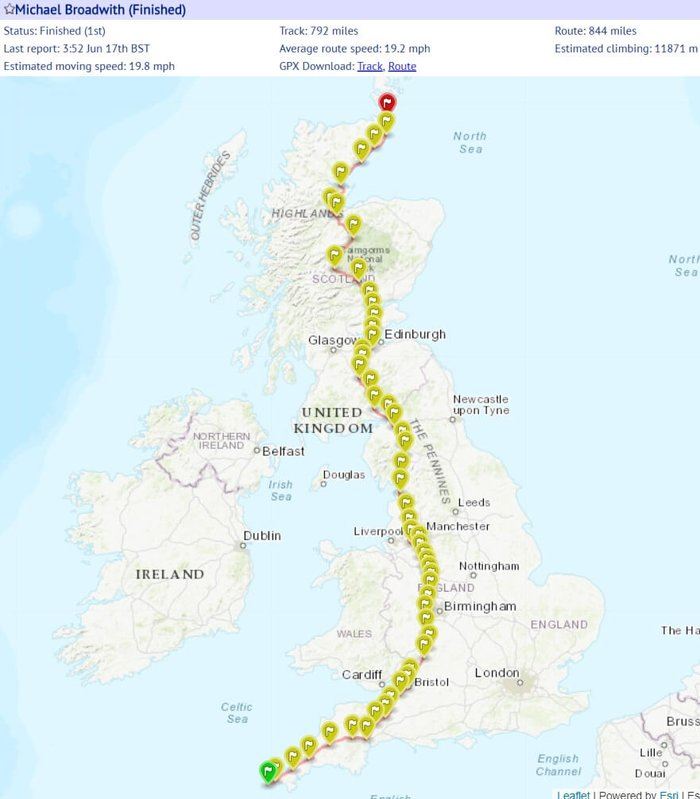
Многие и знать не знают, что такое Край Земли и Джон О’Гроут. На самом деле это реальные географические названия самой южной и самой северной точек Великобритании.
Быстрее всех преодолел этот маршрут на обычном велосипеде Майкл Бродвит в 2018 году за 43 часа 25 минут и 13 секунд.
Рекорд среди женщин не подвергался сомнению с 2002 года и составляет 52 часа 45 минут и 11 секунд, а авторство закреплено за Линн Тейлор.
Правда, есть парняга и побыстрее — Энди Уилкинсон — он проехал тот же маршрут за 41 час 4 минуты и 22 секунды. Единственная загвоздка заключается в том, что он ехал на трехколесном велосипеде располагаясь лежа на спине.
Непонятно только. а много ли это или мало 40-50 часов? Что ж, дистанция составляет 1 406,57 км. Вот и представьте себе график отдыха райдера, который за сутки покрывает почти 700 километров. Некоторым и 20 км в день с трудом поддаются)
4. Самый большой годовой километраж.

Сложно себе даже представить уровень этого достижения, но еще в 1939 году Томми Годвин преодолел за год 120 805,41 км.
Еще раз. За год на велосипеде парень проехал более 120 000 километров. Господа, да многие автомобили не проезжают столько за 5 лет.
Рекорд продержался аж до 2016 года и был побит американцев Куртом Сервогелем, он проехал за год 122 432,7 км. Средняя дистанция за день составляет около 335 километров, и это без выходных.
Тем не менее, 23-летняя девушка, Аманда Кокер сумела проезжать около 380 км за один день. Побить предыдущий женский рекорд ей удалось всего за несколько месяцев, а итог у нее составил 139 326,06 км. Однако и этого Аманде показалось мало, она покорила 100 000 миль (160 934,4 км) за каких-то 423 дня.
Вот, что значит “любить кататься на велосипеде”.
5. Самые большой набор высоты за 48 часов.

Эверестинг — преодоление подъема равного по дистанции высоте Эвереста, происходит заезд многократно на небольшом отрезке с большим уклоном. Термин этот довольно новый, хоть уже и очень популярный, а появился он благодаря приложению Strava.
Однако речь здесь пойдет о 29 623 метрах, которые Крейг Кэннон преодолел за 48 часов в Беркли, штат Калифорния, США.
На фоне 380 км в день, 29 км за двое суток кажутся чем-то невероятно малым. Впрочем, не забывайте, что эти километры были самыми вертикальными, которые себе можно представить.
6. Самое быстрое пересечение Америки.

Гонка через всю Америку (RAAM) считается довольно серьезным испытанием на выносливость. Хотя бы потому, что ее протяженность составляет 4 825 километров. Даже больше, чем пресловутый Тур де Франс.
В 2014 году Кристоф Штрассер справился с дистанцией за 7 дней 15 часов и 56 минут. Учитывая, что маршрут гонки каждый год меняется, было решено рекорд фиксировать, отталкиваясь не от минимального времени преодоления дистанции, а от самой высокой средней скорости. Рекордсменом всё равно остался Штрассер со своими 26,43 км/ч. Кстати, он же является и рекордсменом по количеству побед в RAAM, на его счету уже 6 первых мест.
Фиксируется рекорд по самой высокой средней скорости и среди женщин, он составляет 21,29 км/ч на дистанции в 4 686 км. Побить его никто не может с 1995 года.
7. Самая большая дистанция под водой.

Ну, конечно. Куда ж без этого?)
Если кому-то мало сопротивления от встречного ветра, то отправляйтесь под воду, там вы свой скил прокачаете, как нигде больше.
В 2013 году немецкий велосипедист, Йенс Стотцнер, проехал под водой 6 708 метров, преодолев 78 кругов по дну бассейна для плавания.
Непонятный рекорд, это вам не Америку проехать. и тем не менее, он есть.
8. 8 000 миль в месяц.
Переводим 8 000 миль в километры и получаем 12 874 км за 30 дней.
Рекордсменом в этой области является Аманда наша Кокер. Мы уже о ней рассказывали. Ну, это та, которая проезжает в год больше, чем ты на своем автомобиле за 5 лет.
Так вот, когда Аманда боролась за самые быстрые 100 000 миль, она оказалась быстрее своего предшественника, Стива Абрахама — он проехал 7 104,3 мили (11 433,3 км) за месяц. Аманда за это же время проехала 8 012,5 мили (12 894,87 км). Рекорд состоялся между 1 и 30 апреля 2017 года.
Честно говоря, эти цифры с трудом укладываются в голову. Помнится мне, в самый насыщенный месяц, когда с велосипеда почти не слазил, я проехал аж 800 километров. Всё, больше никому об этом не буду говорить. стыдно же.
9. Кругосветка на велосипеде.

Марк Бомонт в сентябре 2017 года превзошел все предыдущие рекорды, зафиксированные в Книге рекордов Гиннеса. Он проехал кругосветку на велосипеде за 78 дней. Кстати, да, с ним был автомобиль поддержки, но это не умаляет его достижения.
До недавнего времени рекорд был закреплен за Эндрю Николсоном, он проехал кругосветку за 123 дня и 43 минуты.
Однако, правила установления рекорда постоянно редактируются, и теперь, по словам представителей Книги рекордов Гиннеса, минимальное расстояние, которое должно быть преодолено на велосипеде, обязано равняться 29 000 км. Остальная дистанция кругосветки преодолевается при помощи вспомогательного транспорта.
Благодаря постоянным переменам в правилах, в 2012 году рекорд Майкла Холла (91 день и 18 часов) так и не был ратифицирован.
Сорвался также рекорд Ли Фанкура, он проехал кругосветку за 104 дня и 15 минут. Представители Книги отказались его фиксировать из-за того, что Ли, помогая своей команде, взял такси, но в исходную точку так и не вернулся.
В любом случае, фиксировали рекорд представители Книги или нет — неважно. Каждый из них является невероятным испытанием человеческих сил и заслуживает уважения.
10. Самый быстрый wheelie.

Вилли (wheelie) — движение на заднем колесе. Питер Саган любит это дело перед финишем, если только в спринте не участвует.
Итак, самая высокая скорость, с которой велосипедист ехал на заднем колесе, составляет 138,6 км/ч. Рекорд установлен в 2001 году и принадлежит легенде МТБ гонок — Бобби Руту. Разумеется, разгонял велосипед он не своими силами, он следовал за автомобилем. А когда набрал необходимую скорость, то осуществил заветный wheelie. Проехал так он 9,75 м. Не, ну а как? На такой-то скорости дергать руль и так страшно, а он еще и на заднем колесе смог проехать. Так что. даже почти 10 метров это внушительная дистанция.
11. Самое большое расстояние в Zwift без остановок.
Платформа Zwift в рекламе не нуждается, в первые дни ее существования сервера падали несколько раз из-за наплыва желающих покрутить педали онлайн. Конечно, было бы странно, если бы и здесь не было рекордов.
В 2016 году Крис Хопкинсон преодолел 1 625 километров без остановок, чтобы объехать Дерека Бакока. Спустя пару месяцев, 22 февраля 2017 года, Ясмин Мюллер завершил свой трехдневный марафон, во время которого он преодолел дистанцию в 1 828 км.
Борьба разгорелась нешуточная и уже 23 марта Хопкинсон финишировал снова, проехав 2 500 км меньше, чем за 100 часов.
Напомните, пожалуйста, какой такой карантин был в 2016 и 2017 годах? Почему эти рекорды не побиты в 2020 году?) Что такое ели и пили эти рекордсмены, чтобы ехать безостановочно так долго?
12. 24-часовая гонка

По сути, это то же самое, что и часовая гонка, только на целые сутки.
Австриец Кристоф Штрассер, тот который в Америке американцев объехал шесть раз, проехал на велодроме за 24 часа дистанцию в 941,873 км.
Ему пришлось наматывать 3 767 кругов на 250-метровом треке в Гренхене, Швейцария. Средняя скорость составила 39,42 км/ч.
Неутомимому австрийцу, жадному на рекорды, принадлежит такой же рекорд, только реализованный под открытым небом. Здесь он проехал уже 896,173 км.
Задания №11. Задачи на движение по прямой

На этот раз рассматриваем задачи из открытого банка заданий ЕГЭ по математике на прямолинейное движение.
Также смотрите видеолекцию «Текстовые задачи» здесь .
Задачи В14 могут встретиться на ЕГЭ по математике совсем простые, где может даже не потребоваться введение переменной. Чаще будут встречаться задачи, сводимые к решению квадратных уравнений (кстати, что делать, если дискриминант намечается слишком большой, – смотрите здесь и здесь).
Задание 1.
Два велосипедиста одновременно отправились в 130-километровый пробег. Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч.
Пусть км/ч – скорость второго велосипедиста. Тогда согласно условию км/ч – скорость первого велосипедиста.
Оба велосипедиста проехали 130 км.
Третью колонку таблицы заполняем автоматически, пользуясь формулой :
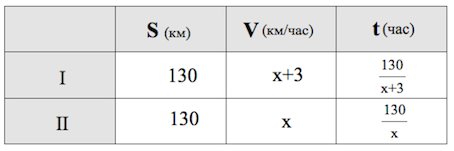
Время движения первого велосипедиста меньше, чем время движения второго на 3 часа, поэтому
Домножаем обе части равенства на , понимая, при этом, что
К финишу придет первым велосипедист со скоростью , поэтому в ответ отправляем величину (км/ч).
Задание 2.
Из пункта А в пункт В, расстояние между которыми 60 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 110 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 5,5 часов позже автомобилиста. Ответ дайте в км/ч.
Задача очень похожа на предыдущую.
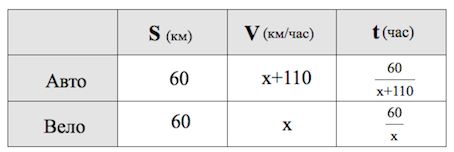
Если не знаете как извлечь корень из большого дискриминанта, загляните сюда и сюда.
Задание 3.
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 80 км. На следующий день он отправился обратно со скоростью на 2 км/ч больше прежней. По дороге он сделал остановку на 2 часа. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
Пусть км/ч – скорость велосипедиста на пути АВ. Тогда согласно условию км/ч – скорость велосипедиста на пути ВА.
Длину пути АВ (ВА) 80 км.
Третью колонку таблицы заполняем автоматически, пользуясь формулой :
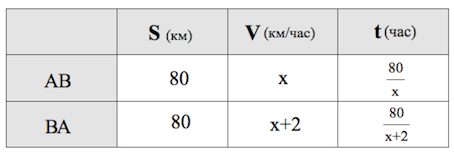
Время движения велосипедиста на пути ВА меньше, чем время движения на пути АВ на 2 часа, поэтому
Откуда вытекает, что (км/ч).
Задание 4.
Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 10 км/ч, а вторую половину пути – со скоростью 60 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 39 км/ч. Ответ дайте в км/ч.
Пусть км/ч – скорость первого автомобиля. Тогда согласно условию км/ч – скорость второго автомобиля на первой половине пути. При этом весь путь считаем км.
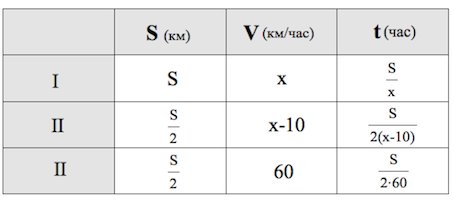
Так как автомобили выехали одновременнно из А и прибыли одновременно в В, то
В условии задачи сказано, что скорость первого автомобиля больше 39 км/ч, поэтому оставляем только вариант
Задание 5.
Из двух городов, расстояние между которыми равно 300 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 70 км/ч и 80 км/ч?
Обозначим за ч время нахождения в пути одного автомобиля до встречи с другим.
Тогда один из автомобилий прошел , второй – км.
В сумме эти пути дают км.
Задание 6.
Из городов A и B, расстояние между которыми равно 300 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 2 часа на расстоянии 160 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч.
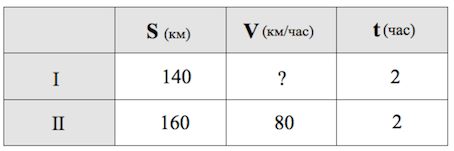
Встреча произошла ближе к А. То есть автомобиль, выехавший из А, проехал меньший путь, нежели автомобиль из В.
Итак, скорость движения автомобиля, выехавшего из А, есть км/ч.
Задание 7.
Расстояние между городами A и B равно 620 км. Из города A в город B выехал первый автомобиль, а через два часа после этого навстречу ему из города B выехал со скоростью 90 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 350 км от города A. Ответ дайте в км/ч.

Второй автомобиль проехал км со скоростью км/ч, значит он находился в пути часа.
Первый автомобиль находился в пути на два часа больше, то есть 5 часов.
Поэтому скорость первого автомобиля, проехавшего км за 5 часов есть км/ч.
Задание 8.
Товарный поезд каждую минуту проезжает на 450 метров меньше, чем скорый, и на путь в 240 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
Прежде всего, переведем м/мин в км/ч.
Обозначаем за км/ч скорость скорого поезда. Тогда скорость товарного – км/ч.
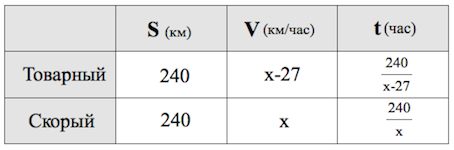
(«Страшные дискриминанты» мы обсуждали здесь)
Откуда Тогда скорость товарного поезда км/ч.
Задание 9.
Расстояние между городами A и B равно 198 км. Из города A в город B выехал автомобиль, а через 3 часа следом за ним со скоростью 80 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.
Пусть расстояние от A до C – км. Так как скорость мотоциклиста км/ч, то время в пути AC мотоциклиста – . По условию сказано, что автомобиль в пути AC находился на 3 часа больше, поэтому указываем в таблице время нахождения автомобиля в пути AC – часов.
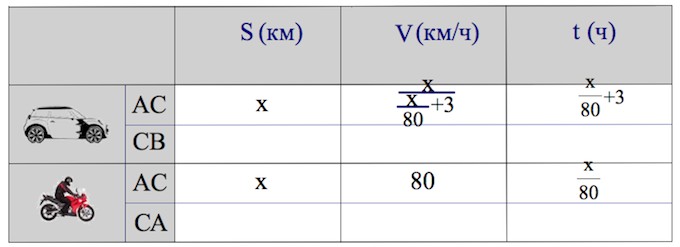
Далее, автомобиль проделывает путь CB, длина которого выражается у нас через , а мотоциклист возвращается обратно, то есть проделывает все тот же путь CA с той же скоростью км/ч за тоже время .
Скорость автомобилиста на пути CB, также как и скорость на пути AC, есть или км/ч.
Поэтому расстояние с этой скоростью он пройдет за время часов.
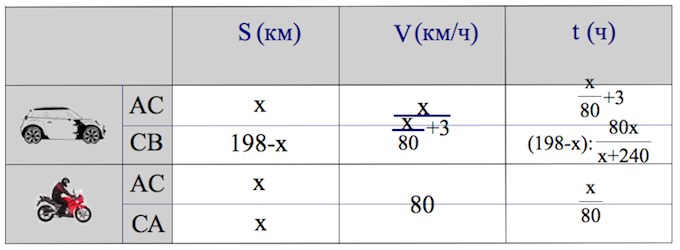
Время прохождения автомобилистом пути CB равно времени прохождения пути CA мотоциклистом, поэтому
Вычисление корня квадратного из большого числа – смотрите здесь.
Задание 10.
Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 475 метрам?
Обозначаем за м/мин скорость второго пешехода и за м – пройденный им путь.
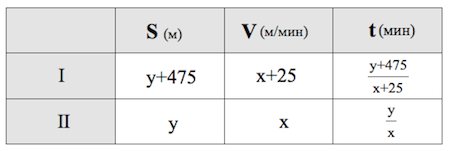
Задание 11.
Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 12 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.
Обозначим за (км/ч) скорость третьего велосипедиста.
Обозначим за (ч) время, прошедшее от старта третьего велосипедиста до встречи со вторым. За это время третий велосипедист проехал км.
Тогда второй находился в пути до встречи с третьим велосипедистом часов и преодолел путь км.
Далее, первый велосипедист, согласно условию, находился в пути часов до встречи второго и третьего велосипедистов и его путь за это время составил
После этого первый, так же как и третий, проехали еще по и км соответственно.
Нам предстоит решить систему:
Конечно же, второй вариант не подходит, так как скорость третьего велосипедиста явно должна быть больше 12 км/ч, иначе он никого не сможет перегнать.
Задание 12.
Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо придорожного столба за 30 секунд. Найдите длину поезда в метрах.
Согласно условию за 30 секунд поезд проходит расстояние, равное своей длине .
Чтобы найти длину поезда , нужно скорость поезда умножить на секунд.
При этом, заметьте, требуется перевод всех данных в один формат.
Задание 13.
Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо лесополосы, длина которой равна 500 метров, за 36 секунд. Найдите длину поезда в метрах.
Согласно условию за 36 минут поезд проходит м, где – длина поезда.
Переведем км/ч в м/мин:
Задание 14.
По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 80 км/ч и 50 км/ч. Длина товарного поезда равна 1200 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 3 минутам. Ответ дайте в метрах.
Переведем сразу км/ч в м/мин:
За 3 минуты товарный поезд прошел м:
а пассажирский (м).
Согласно условию пассажирский поезд за 3 минуты прошел путь, равный м.
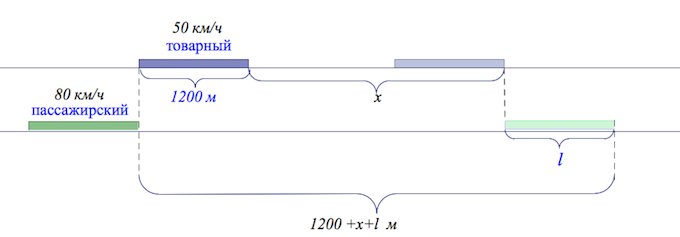
Смотрите фрагмент видеолекции

Побольше оптимизма! И все будет хорошо!

Вы можете пройти тест по задачам на движение по прямой.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
- Задачи №10, часть 1
- Тест по Задачам №11. Задачи на движение
- Задачи №10, часть 3
- Задания №11. Задачи на движение по воде
- Задачи №10 , часть 2
- Задания №11. Задачи на прогрессию
Здравствуйте! В задании 3 у Вас неправильно найдены корни. Ответ должен быть 8.
Неравномерное прямолинейное движение. Средняя скорость
Прямолинейное и равномерное движение возможно лишь на участке пути.
Любое тело со временем меняет свою скорость, как по величине, так и по направлению.
Для описания неравномерного движения его можно разбить на участки, на которых скорость постоянна, и свести задачу к уже известному нам равномерному прямолинейному движению.
Например, пусть велосипедист добрался из города A в город B за 1 час. Первые полчаса он ехал со скоростью 9 км/ч, а потом проколол шину, и вторые полчаса шел пешком со скоростью 3 км/ч.
Направим ось ОХ также от A к B и получим значения проекций скоростей: $$ v_
п.2. Как найти путь и перемещение по графику скорости?
Мы уже знаем, что путь равен площади прямоугольника, который образуется между отрезком графика скорости и отрезком \(\triangle t\) на оси \(t\) (см. §8 данного справочника).
В таком случае, путь велосипедиста в нашем примере:
 \begin
\begin
Общий путь велосипедиста равен 6 км. Расстояние между городами 6 км.
Если принять город A за начало отсчета с \(x_0=0\), то координата велосипедиста в конце пути: $$ x_=x_0+s=0+6=6\ \text $$ Перемещение по оси ОХ: \(\triangle x=x_-x_0=6\ \text\).
Теперь рассмотрим другую ситуацию. Пусть велосипедист выехал из A в B и двигался со скоростью 9 км/ч в течение получаса. Но, после того как проколол шину, он развернулся и пошел пешком назад в A. Где будет находиться велосипедист через полчаса после разворота?
Снова направим ось ОХ от A к B и получим значения проекций скоростей: $$ v_
Путь велосипедиста по-прежнему будет равен сумме площадей прямоугольников, которые образует ломаная \(v_x(t)\) с осью \(t\): \begin 
Если мы учтем знак \(v_
Конечная координата: $$ x_=x_0+\triangle x=0+3=3\ \text $$
Ответ на вопрос задачи найден. Через полчаса после разворота велосипедист будет находиться в точке D в 3 км от города A.
п.3. Средняя скорость и средняя путевая скорость
В нашем примере с велосипедистом, который все время двигался в одну сторону и дошел до города B, получаем: \begin
А вот для случая, когда велосипедист развернулся и пошел обратно: \begin
п.4. Задачи
Задача 1. По графику скоростей найдите среднюю скорость и среднюю путевую скорость движения.
a)
Все движение можно разделить на три участка с постоянной скоростью:
\begin
Общее время: \(t=\triangle t_1+\triangle t_2+\triangle t_3=3+2+2=7\) (с)
Величина средней скорости равна средней путевой скорости: $$ |\overrightarrow
б) 
Все движение можно разделить на три участка с постоянной скоростью:
\begin
Общее перемещение будет меньше общего пути: \begin
Величина средней скорости: $$ |\overrightarrow
Задача 2. Мотоциклист проехал расстояние между двумя пунктами со скоростью 40 км/ч. Потом увеличил скорость до 80 км/ч и проехал расстояние в два раза меньше. Найдите среднюю скорость мотоциклиста за все время движения.
Мотоциклист двигался все время в одном направлении, величина средней скорости равна средней путевой скорости: \(v_
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | 40 | \(\frac=\frac | \(2d\) |
| 2й участок | 80 | \(\frac | \(d\) |
| Сумма | — | \(t=\frac | \(s=2d+d=3d\) |
Упростим сумму дробей: $$ t=\frac
Ответ: 48 км/ч
Задача 3. Автомобиль проехал первую половину пути по шоссе со скоростью 90 км/ч, а вторую половину – по грунтовой дороге со скоростью 30 км/ч. Найдите среднюю скорость автомобиля.
Величина средней скорости равна средней путевой скорости:
\(v_
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | 90 | \(\frac | \(\frac s2\) |
| 2й участок | 30 | \(\frac | \(\frac s2\) |
| Сумма | — | \(t=\frac | \(s\) |
Упростим сумму дробей: $$ t=\frac+\frac=\frac=\frac=\frac $$ Получаем: $$ v_=45\ \text $$
Ответ: 45 км/ч
Задача 4*. Туристы прошли по маршруту со средней скоростью 32 км/ч. Маршрут был разделен на три участка, первый участок преодолевался пешком, второй – на автобусе, третий – на катере. Найдите скорость на каждом участке, если длины этих участков относятся как 1:4:45, а соответствующие интервалы времени как 4:1:20.
Величина средней скорости равна средней путевой скорости:
\(v_
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | \(\frac | \(4t\) | \(d\) |
| 2й участок | \(\frac | \(t\) | \(4d\) |
| 3й участок | \(\frac\) | \(20t\) | \(45d\) |
| Сумма | — | \(25t\) | \(50d\) |
По условию средняя скорость: $$ v_
Ответ: 4 км/ч, 64 км/ч и 36 км/ч
Задача 5*. Первую половину маршрута турист проехал на попутном автомобиле в 10 раз быстрее по сравнению с ходьбой пешком, а вторую половину – на попутном возу в 2 раза медленней. Сэкономил ли турист время на всем маршруте по сравнению с ходьбой пешком?
Пусть \(v\) — скорость туриста при ходьбе пешком.
Найдем среднюю путевую скорость \(v_
Если \(v_
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | \(10v\) | \(\frac | \(\frac s2\) |
| 2й участок | \(\frac | \(\frac | \(\frac s2\) |
| Сумма | — | \(t=\frac | \(s\) |
Упростим сумму дробей: $$ t=\frac+\frac sv=\frac sv\left(\frac+1\right)=\frac\cdot \frac sv $$ Средняя скорость: $$ v_\cdot\frac sv>=\fracv\gt v $$Средняя скорость поездки оказалась меньше пешей скорости туриста.
Значит, он не выиграл по времени.
Ответ: нет
п.5. Лабораторная работа №3. Определение средней скорости движения тела
Цель работы
Научиться определять среднюю скорость движения тела по данным измерений на разных участках. Научиться вычислять абсолютные и относительные погрешности при подстановке данных измерений в формулы.
Теоретические сведения
В лабораторной работе изучается движение тела (шарика) по двум участкам (желобам) с различной скоростью.
Длина участков измеряется с помощью мерной ленты с ценой деления \(\triangle=1\) см,
инструментальная погрешность равна: \(d=\frac=0,5\) см
Абсолютная погрешность измерений при работе с мерной лентой равна инструментальной погрешности, поэтому: \(\triangle s_1=\triangle s_2=d=0,5\) см
Погрешность суммы двух длин: \(\triangle(s_1+s_2)= \triangle s_1+\triangle s_2=2d=1\) см
Измерение времени на каждом участке проводится в сериях их 5 измерений по методике, описанной в Лабораторной работе №2 (см. §4 данного справочника).
Погрешность суммы двух измерений: \(\triangle(t_1+t_2)=\triangle t_1+\triangle t_2\)
Относительная погрешность частного равна сумме относительных погрешностей делимого и делителя: $$ \delta_
Приборы и материалы
Два желоба (не менее 1 м каждый), шарик, мерная лента, секундомер.
Ход работы
1. Ознакомьтесь с теоретической частью работы, выпишите необходимые формулы.
2. Соберите установку, как показано на рисунке. Установите один желоб под углом, другой – горизонтально, закрепите, поставьте в конце горизонтального участка упор. Подберите длину желобов и наклон так, чтобы движение по каждому участку было не менее 1 с.
3. Измерьте фактическую длину каждого участка движения в готовой установке с помощью мерной ленты.
4. Найдите относительную погрешность суммы двух длин \(\delta_
5. Проведите серии по 5 экспериментов для определения \(t_1\) и \(t_2\) с помощью секундомера.
6. Найдите \(\triangle t_1,\ \triangle t_2, \ \triangle(t_1+t_2),\ \delta_
7. По результатам измерений и вычислений найдите \(v_
8. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
1) Измерение длин
Цена деления мерной ленты \(\triangle =1\) см
Инструментальная погрешность мерной ленты \(d=\frac=0,5\) см
Результаты измерений:
\(s_1=112\) cм
\(s_2=208\) cм
Сумма длин участков: \(s_1+s_2=112+208=320\) (см)
Абсолютная погрешность суммы: \(\triangle (s_1+s_2)=\triangle s_1+\triangle s_2=2d=1\) см
Относительная погрешность суммы: $$ \delta_
2) Измерение времени
Цена деления секундомера \(\triangle =0,2\) с
Инструментальная погрешность секундомера \(d=\frac=0,1\) с
Время движения по наклонному желобу
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| \(t_1\) c | 1,5 | 1,6 | 1,5 | 1,4 | 1,4 | 7,4 |
| \(\triangle\) c | 0,02 | 0,12 | 0,02 | 0,08 | 0,08 | 0,32 |
Найдем среднее время спуска с наклонного желоба: $$ t_1=\frac=\frac=1,48\ (c) $$ Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от \(t_1\): $$ \triangle_1=|1,5-1,48|=0,02;\ \triangle_2=|1,6-1,48|=1,02\ \text $$ Среднее абсолютное отклонение: $$ \triangle_
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| \(t_2\) c | 2,3 | 2,4 | 2,2 | 2,2 | 2,4 | 11,5 |
| \(\triangle\) c | 0 | 0,1 | 0,1 | 0,1 | 0,1 | 0,4 |
Найдем среднее время движения по горизонтали: $$ t_2=\frac=\frac=2,3\ (c) $$ Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от \(t_2\): $$ \triangle_1=|2,3-2,3|=0;\ \triangle_2=|2,4-2,3|=0,1\ \text $$ Среднее абсолютное отклонение: $$ \triangle_
3) Расчет погрешности суммы интервалов времени
Сумма интервалов времени: $$ t_1+t_2=1,5+2,3=3,8\ \text $$ Абсолютная погрешность суммы: $$ \triangle(t_1+t_2)=\triangle t_1+\triangle t_2=0,1+0,1=0,2\ \text $$ Относительная погрешность суммы: $$ \delta_
4) Расчет средней скорости $$ v_
Абсолютная ошибка: $$ v_
Выводы
На основании проделанной работы можно сделать следующие выводы.
Измерения длин проводились с помощью мерной ленты. Ошибка измерений равна инструментальной ошибке 0,5 см.
Измерения времени проводились с помощью секундомера. По результатам серий экспериментов ошибка была принята равной инструментальной 0,1 с.
Получена величина средней скорости: \begin
Источники:
http://spacemath.xyz/zadachi-na-dvizhenie/
https://velojournal.net/12-rekordov-v-velosporte
https://egemaximum.ru/13-5/
https://reshator.com/sprav/fizika/7-klass/neravnomernoe-pryamolinejnoe-dvizhenie-srednyaya-skorost/
